Elementare Zahlentheorie

Elementare Zahlentheorie
Jörn Steuding (Uni Würzburg)
Wintersemester 2016/17
D
C
E
A
B
Literaturempfehlungen
• J. Appell, K. Appell: Mengen - Zahlen - Zahlbereiche, Spektrum
2005
• K. Reiss, G. Schmieder: Basiswissen Zahlentheorie, Springer 2007,
2. Auflage
• Nicola Oswald, Jörn Steuding: Elementare Zahlentheorie – Ein
sanfter Einstieg in die höhere Mathematik, Springer 2015
• Roger B. Nelsen: Beweise ohne Worte, herausgegeben von Nicola
Oswald, Springer 2016
§0 Was ist Zahlentheorie?
Ein erstes Beispiel: Mit Quadratzahlen kann man rechte Winkel
konstruieren:
32 + 42 = 52 ,
52 + 122 = 132 ,
...
Das hat Anwendungen beim Bau von Häusern usw. Dies wurde
schon von den Babyloniern vor dreitausend Jahren genutzt!
Im Hintergrund steht die Gleichung
X 2 + Y 2 = Z 2.
Uns interessieren die ganzzahligen Lösungen x, y , z;
diese heißen pythagoräische Tripel.
Wir werden später sehen, wie man solche findet...
§0 Was ist Zahlentheorie?
Ein erstes Beispiel: Mit Quadratzahlen kann man rechte Winkel
konstruieren:
32 + 42 = 52 ,
52 + 122 = 132 ,
...
Das hat Anwendungen beim Bau von Häusern usw. Dies wurde
schon von den Babyloniern vor dreitausend Jahren genutzt!
Im Hintergrund steht die Gleichung
X 2 + Y 2 = Z 2.
Uns interessieren die ganzzahligen Lösungen x, y , z;
diese heißen pythagoräische Tripel.
Wir werden später sehen, wie man solche findet...
§0 Was ist Zahlentheorie?
Ein zweites Beispiel: Es gibt rationale Zahlen (also „Brüche“ , d.h.
Quotienten ganzer Zahlen), wie etwa 1, −5, 13
irrationale
7 usw., und
√
Zahlen (also Zahlen, die nicht rational sind), wie z.B. 2, π.
„rational“ leitet sich von dem lateinischen Wort „ratio“ für
Rechnung, aber auch Vernunft ab: Tatsächlich sind irrationale
√
Zahlen nicht einfach zu begreifen; beispielsweise besitzt 2 eine
unendliche Dezimalbruchentwicklung
√
2 = 1 , 41421 35623 73095 04880 . . . .
Würde man diese irgendwo abhacken (etwa 1, 4), so bekäme √
man
14
7
eine rationale Zahl (nämlich 1, 4 = 10 = 5 ), welche ungleich 2 ist.
Unendlichkeit ist ein schwieriger Begriff in der Mathematik!
§0 Was ist Zahlentheorie?
Ein zweites Beispiel: Es gibt rationale Zahlen (also „Brüche“ , d.h.
Quotienten ganzer Zahlen), wie etwa 1, −5, 13
irrationale
7 usw., und
√
Zahlen (also Zahlen, die nicht rational sind), wie z.B. 2, π.
„rational“ leitet sich von dem lateinischen Wort „ratio“ für
Rechnung, aber auch Vernunft ab: Tatsächlich sind irrationale
√
Zahlen nicht einfach zu begreifen; beispielsweise besitzt 2 eine
unendliche Dezimalbruchentwicklung
√
2 = 1 , 41421 35623 73095 04880 . . . .
Würde man diese irgendwo abhacken (etwa 1, 4), so bekäme √
man
14
7
eine rationale Zahl (nämlich 1, 4 = 10 = 5 ), welche ungleich 2 ist.
Unendlichkeit ist ein schwieriger Begriff in der Mathematik!
§0 Was ist Zahlentheorie?
Ein zweites Beispiel: Es gibt rationale Zahlen (also „Brüche“ , d.h.
Quotienten ganzer Zahlen), wie etwa 1, −5, 13
irrationale
7 usw., und
√
Zahlen (also Zahlen, die nicht rational sind), wie z.B. 2, π.
„rational“ leitet sich von dem lateinischen Wort „ratio“ für
Rechnung, aber auch Vernunft ab: Tatsächlich sind irrationale
√
Zahlen nicht einfach zu begreifen; beispielsweise besitzt 2 eine
unendliche Dezimalbruchentwicklung
√
2 = 1 , 41421 35623 73095 04880 . . . .
Würde man diese irgendwo abhacken (etwa 1, 4), so bekäme √
man
14
7
eine rationale Zahl (nämlich 1, 4 = 10 = 5 ), welche ungleich 2 ist.
Unendlichkeit ist ein schwieriger Begriff in der Mathematik!
§0 Was ist Zahlentheorie?
Ein zweites Beispiel: Es gibt rationale Zahlen (also „Brüche“ , d.h.
Quotienten ganzer Zahlen), wie etwa 1, −5, 13
irrationale
7 usw., und
√
Zahlen (also Zahlen, die nicht rational sind), wie z.B. 2, π.
„rational“ leitet sich von dem lateinischen Wort „ratio“ für
Rechnung, aber auch Vernunft ab: Tatsächlich sind irrationale
√
Zahlen nicht einfach zu begreifen; beispielsweise besitzt 2 eine
unendliche Dezimalbruchentwicklung
√
2 = 1 , 41421 35623 73095 04880 . . . .
Würde man diese irgendwo abhacken (etwa 1, 4), so bekäme √
man
14
7
eine rationale Zahl (nämlich 1, 4 = 10 = 5 ), welche ungleich 2 ist.
Unendlichkeit ist ein schwieriger Begriff in der Mathematik!
§0 Was ist Zahlentheorie?
In der Mathematik müssen Aussagen bewiesen werden.
Hier ein erstes Beispiel:
√
Satz 0.1 2 ist irrational.
√
Ein Beweis ohne Worte für die Irrationalität von 2:
D
C
E
A
B
§0 Was ist Zahlentheorie?
In der Mathematik müssen Aussagen bewiesen werden.
Hier ein erstes Beispiel:
√
Satz 0.1 2 ist irrational.
√
Ein Beweis ohne Worte für die Irrationalität von 2:
D
C
E
A
B
§0 Was ist Zahlentheorie?
In der Mathematik müssen Aussagen bewiesen werden.
Hier ein erstes Beispiel:
√
Satz 0.1 2 ist irrational.
√
Ein Beweis ohne Worte für die Irrationalität von 2:
D
C
E
A
B
§0 Was ist Zahlentheorie?
Bezeichnet b die√Kantenlänge des großen Quadrates, so ist nach
Pythagoras a = 2b die Länge der Diagonalen. Der Schnittpunkt
E des Achtelkreises um A vom Radius b mit der Diagonalen
definiert eine Strecke der Länge a − b. Wird auf dieser ein Quadrat
errichtet, so liegen zwei Ecken desselben auf einer Kante des alten
Quadrates und 2b − a ist die Länge der Diagonalen des neuen
Quadrates. Daraus ergibt sich für die jeweiligen Proportionen von
Diagonale und Kante in den beiden Quadraten
√
2=
2b − a
a
=
.
b
a−b
Angenommen, a und b seien natürliche Zahlen, wobei b minimal
sei, so folgt 0 < a − b < b, was der Minimalität von b widerspricht.
Wir werden später noch andere Irrationalzahlen kennenlernen...
§0 Was ist Zahlentheorie?
Bezeichnet b die√Kantenlänge des großen Quadrates, so ist nach
Pythagoras a = 2b die Länge der Diagonalen. Der Schnittpunkt
E des Achtelkreises um A vom Radius b mit der Diagonalen
definiert eine Strecke der Länge a − b. Wird auf dieser ein Quadrat
errichtet, so liegen zwei Ecken desselben auf einer Kante des alten
Quadrates und 2b − a ist die Länge der Diagonalen des neuen
Quadrates. Daraus ergibt sich für die jeweiligen Proportionen von
Diagonale und Kante in den beiden Quadraten
√
2=
2b − a
a
=
.
b
a−b
Angenommen, a und b seien natürliche Zahlen, wobei b minimal
sei, so folgt 0 < a − b < b, was der Minimalität von b widerspricht.
Wir werden später noch andere Irrationalzahlen kennenlernen...
§0 Was ist Zahlentheorie?
Welche der folgenden Gleichungen besitzt Lösungen x, y in ganzen
Zahlen?
• 2X − 5Y = 0
• X 2 − 2Y 2 = 0
• X 2 − 2Y 2 = 1
Welche geometrischen Objekte stecken hinter diesen Gleichungen?
Und wie findet man alle Punkte mit ganzzahligen Koordinaten auf
den jeweiligen Kurven?
§0 Was ist Zahlentheorie?
Welche der folgenden Gleichungen besitzt Lösungen x, y in ganzen
Zahlen?
• 2X − 5Y = 0
• X 2 − 2Y 2 = 0
• X 2 − 2Y 2 = 1
Welche geometrischen Objekte stecken hinter diesen Gleichungen?
Und wie findet man alle Punkte mit ganzzahligen Koordinaten auf
den jeweiligen Kurven?
Resümee
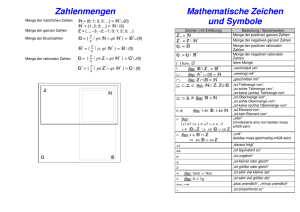
Wir unterscheiden verschiedene Mengen von Zahlen:
• N = {1, 2, 3, . . .} ist die Menge der natürlichen Zahlen,
• Z = {. . . , −2, −1, 0, 1, 2, 3, . . .} die Menge der ganzen Zahlen,
• Q = { ba : a ∈ Z, b ∈ N} die Menge der rationalen Zahlen, und
neben den
• R bezeichnet die Menge der reellen Zahlen, welche
√ √
rationalen Zahlen auch Irrationalzahlen wie etwas 2, 3 enthält.
Mit einem indirekten Beweis verifiziert man eine Aussage, in dem
man die negierte Aussage zu einem Widerspruch führt.
Das weitere Programm
I. Grundlagen behandelt Sprache und Aufbau der Mathematik,
insbesondere Logik und Mengen, sowie ganze und rationale Zahlen
II. Teilbarkeitslehre und die Rolle der Primzahlen
III. Modulare Arithmetik ist Rechnen mit Resten
IV. Das Kontinuum gibt Aufschluss über die reellen Zahlen
V. Diophantische Approximation mit weiteren Irrationalzahlen
VI. Diophantische Gleichungen incl. pythagoräische Tripel
VII. Komplexe Zahlen – eine imaginäre Welt :-)
I. Grundlagen
§1 Elementare Logik und Mengenlehre
Bausteine der Mathematik sind Definitionen mathematischer
Objekte, Aussagen zu ebensolchen und Schlussfolgerungen hieraus.
Aussagen werden in zwei verschiedene Schubfächer verteilt, je
nachdem ob sie wahr (w ) oder falsch (f ) sind. Beispielsweise
A: Es gibt eine gerade Primzahl.
oder
B: Alle Primzahlen sind ungerade.
Aussage B ist die Negation von Aussage A, was wir auch mit
B = ¬A notieren. Übrigens ist B unwahr, denn 2 ist eine Primzahl
und gerade, was zeigt, dass A wahr ist. Man sagt auch, dass die
gerade Primzahl 2 ein Gegenbeispiel für Aussage B ist.
§1 Elementare Logik und Mengenlehre
Bausteine der Mathematik sind Definitionen mathematischer
Objekte, Aussagen zu ebensolchen und Schlussfolgerungen hieraus.
Aussagen werden in zwei verschiedene Schubfächer verteilt, je
nachdem ob sie wahr (w ) oder falsch (f ) sind. Beispielsweise
A: Es gibt eine gerade Primzahl.
oder
B: Alle Primzahlen sind ungerade.
Aussage B ist die Negation von Aussage A, was wir auch mit
B = ¬A notieren. Übrigens ist B unwahr, denn 2 ist eine Primzahl
und gerade, was zeigt, dass A wahr ist. Man sagt auch, dass die
gerade Primzahl 2 ein Gegenbeispiel für Aussage B ist.
§1 Elementare Logik und Mengenlehre
Bausteine der Mathematik sind Definitionen mathematischer
Objekte, Aussagen zu ebensolchen und Schlussfolgerungen hieraus.
Aussagen werden in zwei verschiedene Schubfächer verteilt, je
nachdem ob sie wahr (w ) oder falsch (f ) sind. Beispielsweise
A: Es gibt eine gerade Primzahl.
oder
B: Alle Primzahlen sind ungerade.
Aussage B ist die Negation von Aussage A, was wir auch mit
B = ¬A notieren. Übrigens ist B unwahr, denn 2 ist eine Primzahl
und gerade, was zeigt, dass A wahr ist. Man sagt auch, dass die
gerade Primzahl 2 ein Gegenbeispiel für Aussage B ist.
§1 Elementare Logik und Mengenlehre
Bausteine der Mathematik sind Definitionen mathematischer
Objekte, Aussagen zu ebensolchen und Schlussfolgerungen hieraus.
Aussagen werden in zwei verschiedene Schubfächer verteilt, je
nachdem ob sie wahr (w ) oder falsch (f ) sind. Beispielsweise
A: Es gibt eine gerade Primzahl.
oder
B: Alle Primzahlen sind ungerade.
Aussage B ist die Negation von Aussage A, was wir auch mit
B = ¬A notieren. Übrigens ist B unwahr, denn 2 ist eine Primzahl
und gerade, was zeigt, dass A wahr ist. Man sagt auch, dass die
gerade Primzahl 2 ein Gegenbeispiel für Aussage B ist.
§1 Elementare Logik und Mengenlehre
Problematisch sind Aussagen wie
Das Wetter ist schön,
weil dieser Behauptung nicht ohne weiteres ein Wahrheitsgehalt
zugeordnet werden kann.
Interessant sind auch Aussagen, von denen a priori nicht bekannt
ist, ob sie denn wahr oder falsch sind, wie etwa:
C: Jede gerade Zahl größer oder gleich vier lässt
sich als Summe von zwei Primzahlen schreiben.
Tatsächlich ist C eine offene Vermutung der Zahlentheorie. Hier
kann man versuchen, mit logischen Schlüssen einen Beweis für die
Wahrheit oder einen Nachweis für die Unwahrheit zu finden.
Intuitiv dürfte dabei klar sein, was hier ’logische Schlüsse’ sind.
§1 Elementare Logik und Mengenlehre
Problematisch sind Aussagen wie
Das Wetter ist schön,
weil dieser Behauptung nicht ohne weiteres ein Wahrheitsgehalt
zugeordnet werden kann.
Interessant sind auch Aussagen, von denen a priori nicht bekannt
ist, ob sie denn wahr oder falsch sind, wie etwa:
C: Jede gerade Zahl größer oder gleich vier lässt
sich als Summe von zwei Primzahlen schreiben.
Tatsächlich ist C eine offene Vermutung der Zahlentheorie. Hier
kann man versuchen, mit logischen Schlüssen einen Beweis für die
Wahrheit oder einen Nachweis für die Unwahrheit zu finden.
Intuitiv dürfte dabei klar sein, was hier ’logische Schlüsse’ sind.
§1 Elementare Logik und Mengenlehre
Hier ein illustrierendes Beispiel, welches sich durch die ’richtige’
Logik lösen lässt:
Eine Knobelaufgabe: Drei Logikerinnen sitzen auf Stühlen
hintereinander; die hinterste sieht die beiden vorderen, die mittlere
nur die vorderste und die vorderste sieht niemanden. Alle drei
wissen, dass sie jeweils einen Hut aus einer Menge von drei
schwarzen und zwei roten Hüten aufsitzen haben. Die hinterste
Logikerin wird gefragt, ob sie ihre Hutfarbe kenne. Nachdem sie
verneint wird die mittlere das Gleiche gefragt, worauf auch diese
verneint. Schließlich wird die vorderste gefragt. Was antwortet
diese?
§1 Elementare Logik und Mengenlehre
Was läuft hier falsch?
−2 = −2
1−3 = 4−6
9
4
− 32 )2
1 − 23
1−3+
(1
= 4−6+
9
4
= (2 − 32 )2
= 2−
3
2
1 = 2
Die Argumentation verläuft von oben nach unten; sie startet mit
einer wahren Aussage und endet mit einer falschen. Beim Schritt
von der ersten zur zweiten Zeile wird beispielsweise auf jeder Seite
1 − 1 = 0 bzw. 4 − 4 = 0 addiert. In der Mathematik ist bei jedem
Argument, bei jedem Beweis, eine gesunde Skepsis besser als ein
unbedingter Glaube in das gedruckte Wort!
§1 Elementare Logik und Mengenlehre
Was läuft hier falsch?
−2 = −2
1−3 = 4−6
9
4
− 32 )2
1 − 23
1−3+
(1
= 4−6+
9
4
= (2 − 32 )2
= 2−
3
2
1 = 2
Die Argumentation verläuft von oben nach unten; sie startet mit
einer wahren Aussage und endet mit einer falschen. Beim Schritt
von der ersten zur zweiten Zeile wird beispielsweise auf jeder Seite
1 − 1 = 0 bzw. 4 − 4 = 0 addiert. In der Mathematik ist bei jedem
Argument, bei jedem Beweis, eine gesunde Skepsis besser als ein
unbedingter Glaube in das gedruckte Wort!
§1 Elementare Logik und Mengenlehre
Was läuft hier falsch?
−2 = −2
1−3 = 4−6
9
4
− 32 )2
1 − 23
1−3+
(1
= 4−6+
9
4
= (2 − 32 )2
= 2−
3
2
1 = 2
Die Argumentation verläuft von oben nach unten; sie startet mit
einer wahren Aussage und endet mit einer falschen. Beim Schritt
von der ersten zur zweiten Zeile wird beispielsweise auf jeder Seite
1 − 1 = 0 bzw. 4 − 4 = 0 addiert. In der Mathematik ist bei jedem
Argument, bei jedem Beweis, eine gesunde Skepsis besser als ein
unbedingter Glaube in das gedruckte Wort!
§1 Elementare Logik und Mengenlehre
Gegeben zwei Aussagen A und B, können diese folgendermaßen zu
neuen Aussagen verknüpft werden:
die Konjunktion A und B:
die Disjunktion A oder B:
die Implikation:
A∧B ;
A∨B ;
A⇒B ,
d.h. A impliziert B (bzw. aus A folgt B);
die Äquivalenz :
A ⇐⇒ B ,
d.h. A und B sind äquivalent (also A ⇒ B und B ⇒ A).
§1 Elementare Logik und Mengenlehre
Gegeben zwei Aussagen A und B, können diese folgendermaßen zu
neuen Aussagen verknüpft werden:
die Konjunktion A und B:
die Disjunktion A oder B:
die Implikation:
A∧B ;
A∨B ;
A⇒B ,
d.h. A impliziert B (bzw. aus A folgt B);
die Äquivalenz :
A ⇐⇒ B ,
d.h. A und B sind äquivalent (also A ⇒ B und B ⇒ A).
§1 Elementare Logik und Mengenlehre
Gegeben zwei Aussagen A und B, können diese folgendermaßen zu
neuen Aussagen verknüpft werden:
die Konjunktion A und B:
die Disjunktion A oder B:
die Implikation:
A∧B ;
A∨B ;
A⇒B ,
d.h. A impliziert B (bzw. aus A folgt B);
die Äquivalenz :
A ⇐⇒ B ,
d.h. A und B sind äquivalent (also A ⇒ B und B ⇒ A).
§1 Elementare Logik und Mengenlehre
Gegeben zwei Aussagen A und B, können diese folgendermaßen zu
neuen Aussagen verknüpft werden:
die Konjunktion A und B:
die Disjunktion A oder B:
die Implikation:
A∧B ;
A∨B ;
A⇒B ,
d.h. A impliziert B (bzw. aus A folgt B);
die Äquivalenz :
A ⇐⇒ B ,
d.h. A und B sind äquivalent (also A ⇒ B und B ⇒ A).
§1 Elementare Logik und Mengenlehre
Mit einer Wahrheitstafel lassen sich die verschiendenen
Verknüpfungen gut miteinander vergleichen:
A
w
w
f
f
B
w
f
w
f
¬A
f
f
w
w
¬B
f
w
f
w
A⇒B
w
f
w
w
¬B ⇒ ¬A
w
f
w
w
Die letzten beiden Spalten zeigen eine so genannte Kontraposition,
nämlich wie mit der Widerlegung der Negation einer Aussage
dieselbe indirekt bewiesen wird.
§1 Elementare Logik und Mengenlehre
Mit einer Wahrheitstafel lassen sich die verschiendenen
Verknüpfungen gut miteinander vergleichen:
A
w
w
f
f
B
w
f
w
f
¬A
f
f
w
w
¬B
f
w
f
w
A⇒B
w
f
w
w
¬B ⇒ ¬A
w
f
w
w
Die letzten beiden Spalten zeigen eine so genannte Kontraposition,
nämlich wie mit der Widerlegung der Negation einer Aussage
dieselbe indirekt bewiesen wird.
§1 Elementare Logik und Mengenlehre
Der Begründer der Mengenlehre Georg Cantor legte seiner Theorie
folgende Definition zu Grunde:
”Unter einer Menge verstehen wir jede Zusammenfassung
von bestimmten, wohl unterschiedenen Objekten unserer
Anschauung und unseres Denkens zu einem Ganzen.”
Die Objekte einer Menge heißen Elemente. Ist M eine Menge und x
ein Element von M, so schreiben wir x ∈ M und sagen ’x gehört zu
M’ oder ’x liegt in M’; ist hingegen x kein Element von M, so
schreiben wir x ∈
/ M.
Eine Menge kann durch Aufzählung ihrer Elemente beschrieben
werden, z.B.
N = {1, 2, 3, 4, . . .},
wobei N unendlich viele Elemente besitzt, wir aber nur endlich viele
von diesen tatsächlich hinschreiben können.
§1 Elementare Logik und Mengenlehre
Der Begründer der Mengenlehre Georg Cantor legte seiner Theorie
folgende Definition zu Grunde:
”Unter einer Menge verstehen wir jede Zusammenfassung
von bestimmten, wohl unterschiedenen Objekten unserer
Anschauung und unseres Denkens zu einem Ganzen.”
Die Objekte einer Menge heißen Elemente. Ist M eine Menge und x
ein Element von M, so schreiben wir x ∈ M und sagen ’x gehört zu
M’ oder ’x liegt in M’; ist hingegen x kein Element von M, so
schreiben wir x ∈
/ M.
Eine Menge kann durch Aufzählung ihrer Elemente beschrieben
werden, z.B.
N = {1, 2, 3, 4, . . .},
wobei N unendlich viele Elemente besitzt, wir aber nur endlich viele
von diesen tatsächlich hinschreiben können.
§1 Elementare Logik und Mengenlehre
Der Begründer der Mengenlehre Georg Cantor legte seiner Theorie
folgende Definition zu Grunde:
”Unter einer Menge verstehen wir jede Zusammenfassung
von bestimmten, wohl unterschiedenen Objekten unserer
Anschauung und unseres Denkens zu einem Ganzen.”
Die Objekte einer Menge heißen Elemente. Ist M eine Menge und x
ein Element von M, so schreiben wir x ∈ M und sagen ’x gehört zu
M’ oder ’x liegt in M’; ist hingegen x kein Element von M, so
schreiben wir x ∈
/ M.
Eine Menge kann durch Aufzählung ihrer Elemente beschrieben
werden, z.B.
N = {1, 2, 3, 4, . . .},
wobei N unendlich viele Elemente besitzt, wir aber nur endlich viele
von diesen tatsächlich hinschreiben können.
§1 Elementare Logik und Mengenlehre
Ferner kann man Mengen durch Angabe einer Eigenschaft
definieren, z.B.
P := {p : p ist Primzahl}.
Hierbei deutet das Symbol ’:=’ an, dass die linke Seite durch die
rechte definiert wird, wir also im Folgenden mit
P = {2, 3, 5, 7, 11, 13, . . .}
die Menge der Primzahlen bezeichnen.
Tatsächlich gleicht die Mathematik ein wenig einer Fremdsprache
und die Liste ihrer Definitionen einem Vokabelheft.
§1 Elementare Logik und Mengenlehre
Ferner kann man Mengen durch Angabe einer Eigenschaft
definieren, z.B.
P := {p : p ist Primzahl}.
Hierbei deutet das Symbol ’:=’ an, dass die linke Seite durch die
rechte definiert wird, wir also im Folgenden mit
P = {2, 3, 5, 7, 11, 13, . . .}
die Menge der Primzahlen bezeichnen.
Tatsächlich gleicht die Mathematik ein wenig einer Fremdsprache
und die Liste ihrer Definitionen einem Vokabelheft.
§1 Elementare Logik und Mengenlehre
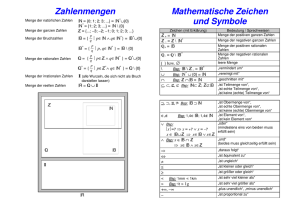
Zwei Mengen M und N sind gleich, d.h. M = N, wenn sie dieselben
Elemente haben. Ferner heißt eine Menge M Teilmenge von N, in
Zeichen M ⊂ N, falls jedes Element von M auch ein Element von
N ist. Beispielsweise gilt
P ⊂ N ⊂ Z.
Gleichheit von Mengen M und N zeigt man oft durch die
Mengeninklusionen M ⊂ N und N ⊂ M, also
M⊂N
und
N⊂M
⇒
M = N.
⇒
M ⊂ L.
Ferner gilt für Teilmengen von Teilmengen
M⊂N
und
N⊂L
§1 Elementare Logik und Mengenlehre
Zwei Mengen M und N sind gleich, d.h. M = N, wenn sie dieselben
Elemente haben. Ferner heißt eine Menge M Teilmenge von N, in
Zeichen M ⊂ N, falls jedes Element von M auch ein Element von
N ist. Beispielsweise gilt
P ⊂ N ⊂ Z.
Gleichheit von Mengen M und N zeigt man oft durch die
Mengeninklusionen M ⊂ N und N ⊂ M, also
M⊂N
und
N⊂M
⇒
M = N.
⇒
M ⊂ L.
Ferner gilt für Teilmengen von Teilmengen
M⊂N
und
N⊂L
§1 Elementare Logik und Mengenlehre
Zwei Mengen M und N sind gleich, d.h. M = N, wenn sie dieselben
Elemente haben. Ferner heißt eine Menge M Teilmenge von N, in
Zeichen M ⊂ N, falls jedes Element von M auch ein Element von
N ist. Beispielsweise gilt
P ⊂ N ⊂ Z.
Gleichheit von Mengen M und N zeigt man oft durch die
Mengeninklusionen M ⊂ N und N ⊂ M, also
M⊂N
und
N⊂M
⇒
M = N.
⇒
M ⊂ L.
Ferner gilt für Teilmengen von Teilmengen
M⊂N
und
N⊂L
§1 Elementare Logik und Mengenlehre
Zwei Mengen M und N sind gleich, d.h. M = N, wenn sie dieselben
Elemente haben. Ferner heißt eine Menge M Teilmenge von N, in
Zeichen M ⊂ N, falls jedes Element von M auch ein Element von
N ist. Beispielsweise gilt
P ⊂ N ⊂ Z.
Gleichheit von Mengen M und N zeigt man oft durch die
Mengeninklusionen M ⊂ N und N ⊂ M, also
M⊂N
und
N⊂M
⇒
M = N.
⇒
M ⊂ L.
Ferner gilt für Teilmengen von Teilmengen
M⊂N
und
N⊂L
§1 Elementare Logik und Mengenlehre
Eine Definition beschreibt möglichst schnörkellos und in eindeutiger
Weise einen Begriff oder ein Objekt unseres mathematischen
Denkens; erst nach einer solchen Definition darf das zu Grunde
liegende Objekt in einer Aussage oder einem Beweis benutzt
werden.
Hier ein Beispiel eines (nicht ganz einfachen) Objektes: Die leere
Menge ist erklärt durch ∅ := {x ∈ M : x 6= x}, wobei M irgendeine
Menge sei. Die leere Menge ist eindeutig bestimmt und hängt nicht
von M ab. Es gilt ∅ ⊂ M; sie ist also Teilmenge jeder Menge,
enthält aber selbst kein Element.
Die Potenzmenge von M, welche wir als 2M notieren, ist die Menge
aller Teilmengen von M, also
2M = {N : N ⊂ M}.
Insbesondere gilt M = {0, 1}, dann 2M = {∅, {0}, {1}, M}.
§1 Elementare Logik und Mengenlehre
Eine Definition beschreibt möglichst schnörkellos und in eindeutiger
Weise einen Begriff oder ein Objekt unseres mathematischen
Denkens; erst nach einer solchen Definition darf das zu Grunde
liegende Objekt in einer Aussage oder einem Beweis benutzt
werden.
Hier ein Beispiel eines (nicht ganz einfachen) Objektes: Die leere
Menge ist erklärt durch ∅ := {x ∈ M : x 6= x}, wobei M irgendeine
Menge sei. Die leere Menge ist eindeutig bestimmt und hängt nicht
von M ab. Es gilt ∅ ⊂ M; sie ist also Teilmenge jeder Menge,
enthält aber selbst kein Element.
Die Potenzmenge von M, welche wir als 2M notieren, ist die Menge
aller Teilmengen von M, also
2M = {N : N ⊂ M}.
Insbesondere gilt M = {0, 1}, dann 2M = {∅, {0}, {1}, M}.
§1 Elementare Logik und Mengenlehre
Eine Definition beschreibt möglichst schnörkellos und in eindeutiger
Weise einen Begriff oder ein Objekt unseres mathematischen
Denkens; erst nach einer solchen Definition darf das zu Grunde
liegende Objekt in einer Aussage oder einem Beweis benutzt
werden.
Hier ein Beispiel eines (nicht ganz einfachen) Objektes: Die leere
Menge ist erklärt durch ∅ := {x ∈ M : x 6= x}, wobei M irgendeine
Menge sei. Die leere Menge ist eindeutig bestimmt und hängt nicht
von M ab. Es gilt ∅ ⊂ M; sie ist also Teilmenge jeder Menge,
enthält aber selbst kein Element.
Die Potenzmenge von M, welche wir als 2M notieren, ist die Menge
aller Teilmengen von M, also
2M = {N : N ⊂ M}.
Insbesondere gilt M = {0, 1}, dann 2M = {∅, {0}, {1}, M}.
§1 Elementare Logik und Mengenlehre
Eine Definition beschreibt möglichst schnörkellos und in eindeutiger
Weise einen Begriff oder ein Objekt unseres mathematischen
Denkens; erst nach einer solchen Definition darf das zu Grunde
liegende Objekt in einer Aussage oder einem Beweis benutzt
werden.
Hier ein Beispiel eines (nicht ganz einfachen) Objektes: Die leere
Menge ist erklärt durch ∅ := {x ∈ M : x 6= x}, wobei M irgendeine
Menge sei. Die leere Menge ist eindeutig bestimmt und hängt nicht
von M ab. Es gilt ∅ ⊂ M; sie ist also Teilmenge jeder Menge,
enthält aber selbst kein Element.
Die Potenzmenge von M, welche wir als 2M notieren, ist die Menge
aller Teilmengen von M, also
2M = {N : N ⊂ M}.
Insbesondere gilt M = {0, 1}, dann 2M = {∅, {0}, {1}, M}.
§1 Elementare Logik und Mengenlehre
Eine Definition beschreibt möglichst schnörkellos und in eindeutiger
Weise einen Begriff oder ein Objekt unseres mathematischen
Denkens; erst nach einer solchen Definition darf das zu Grunde
liegende Objekt in einer Aussage oder einem Beweis benutzt
werden.
Hier ein Beispiel eines (nicht ganz einfachen) Objektes: Die leere
Menge ist erklärt durch ∅ := {x ∈ M : x 6= x}, wobei M irgendeine
Menge sei. Die leere Menge ist eindeutig bestimmt und hängt nicht
von M ab. Es gilt ∅ ⊂ M; sie ist also Teilmenge jeder Menge,
enthält aber selbst kein Element.
Die Potenzmenge von M, welche wir als 2M notieren, ist die Menge
aller Teilmengen von M, also
2M = {N : N ⊂ M}.
Insbesondere gilt M = {0, 1}, dann 2M = {∅, {0}, {1}, M}.
§1 Elementare Logik und Mengenlehre
Mit Mengen sind eine Reihe von Operationen möglich: Die
Vereinigung
M ∪ N := {x : x ∈ M ∨ x ∈ N}
zweier Mengen M, N besteht sowohl aus den Elementen von M als
auch aus denen von N. Somit ist
Z = N ∪ {−n : n ∈ N} ∪ {0}.
Der Durchschnitt
M ∩ N := {x | x ∈ M ∧ x ∈ N}
zweier Mengen M, N ist die Menge aller Elemente, die sowohl zu M
als auch zu N gehören. Z.B. ist
{2} = P ∩ {n ∈ Z : n ist gerade}.
§1 Elementare Logik und Mengenlehre
Mit Mengen sind eine Reihe von Operationen möglich: Die
Vereinigung
M ∪ N := {x : x ∈ M ∨ x ∈ N}
zweier Mengen M, N besteht sowohl aus den Elementen von M als
auch aus denen von N. Somit ist
Z = N ∪ {−n : n ∈ N} ∪ {0}.
Der Durchschnitt
M ∩ N := {x | x ∈ M ∧ x ∈ N}
zweier Mengen M, N ist die Menge aller Elemente, die sowohl zu M
als auch zu N gehören. Z.B. ist
{2} = P ∩ {n ∈ Z : n ist gerade}.
§1 Elementare Logik und Mengenlehre
So genannte Venn-Diagramme (nach John Venn) sind nützlich zur
Veranschaulichung:
Das Komplement einer Menge N in M (oder die Differenz von M
und N) ist die Menge
M\N := {x : x ∈ M ∧ x ∈
/ N}
und besteht aus allen Elementen von M, die nicht zu N gehören.
§1 Elementare Logik und Mengenlehre
So genannte Venn-Diagramme (nach John Venn) sind nützlich zur
Veranschaulichung:
Das Komplement einer Menge N in M (oder die Differenz von M
und N) ist die Menge
M\N := {x : x ∈ M ∧ x ∈
/ N}
und besteht aus allen Elementen von M, die nicht zu N gehören.
§1 Elementare Logik und Mengenlehre
Mit Mengen kann man ähnlich umgehen wie mit Aussagen. Dies
verdeutlicht etwas Mengenalgebra:
M\M = ∅,
M\∅ = M,
M ∩ M = M,
M ∪ M = M.
Wiederum gelten Vertauschungs- und Verknüpfungsregeln:
Kommutativität:
M ∪N = N ∪M
Assoziativität:
und
M ∩ N = N ∩ M.
(M ∪ N) ∪ L = M ∪ (N ∪ L),
(M ∩ N) ∩ L = M ∩ (N ∩ L).
Distributivität:
(M ∩ N) ∪ L = (M ∪ L) ∩ (M ∪ L),
(M ∪ N) ∩ L = (M ∩ L) ∪ (M ∩ L).
§1 Elementare Logik und Mengenlehre
Mit Mengen kann man ähnlich umgehen wie mit Aussagen. Dies
verdeutlicht etwas Mengenalgebra:
M\M = ∅,
M\∅ = M,
M ∩ M = M,
M ∪ M = M.
Wiederum gelten Vertauschungs- und Verknüpfungsregeln:
Kommutativität:
M ∪N = N ∪M
Assoziativität:
und
M ∩ N = N ∩ M.
(M ∪ N) ∪ L = M ∪ (N ∪ L),
(M ∩ N) ∩ L = M ∩ (N ∩ L).
Distributivität:
(M ∩ N) ∪ L = (M ∪ L) ∩ (M ∪ L),
(M ∪ N) ∩ L = (M ∩ L) ∪ (M ∩ L).
§1 Elementare Logik und Mengenlehre
Mit Mengen kann man ähnlich umgehen wie mit Aussagen. Dies
verdeutlicht etwas Mengenalgebra:
M\M = ∅,
M\∅ = M,
M ∩ M = M,
M ∪ M = M.
Wiederum gelten Vertauschungs- und Verknüpfungsregeln:
Kommutativität:
M ∪N = N ∪M
Assoziativität:
und
M ∩ N = N ∩ M.
(M ∪ N) ∪ L = M ∪ (N ∪ L),
(M ∩ N) ∩ L = M ∩ (N ∩ L).
Distributivität:
(M ∩ N) ∪ L = (M ∪ L) ∩ (M ∪ L),
(M ∪ N) ∩ L = (M ∩ L) ∪ (M ∩ L).
§1 Elementare Logik und Mengenlehre
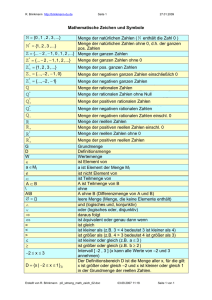
Satz 1.1 (de Morgansche Formeln) Für irgendwelche
Teilmengen M, N einer beliebigen Menge X gelten
X \(M ∩ N) = (X \M) ∪ (X \N),
X \(M ∪ N) = (X \M) ∩ (X \N);
Diese Formeln sind in ihrer Erscheinungsform völlig analog zu den
de Morganschen Regeln der Aussagenlogik (s.o.), deshalb tragen sie
auch denselben Namen. So ist etwa die erste ganz ähnlich zu
¬(A ∧ B)
⇔
¬A ∨ ¬B,
wenn man nämlich mit A die Aussage ’x ∈ M’ und mit B die
Aussage ’x ∈ N’ belegt. Insofern können wir obigen Satz auf die de
Morganschen Regeln der Aussagenlogik zurück führen.
§1 Elementare Logik und Mengenlehre
Das kartesische Produkt zweier Mengen M, N ist die Menge
M × N := {(x, y ) : x ∈ M, y ∈ N}.
Hierfür gelten:
(M1 ∩ M2 ) × N = (M1 × N) ∩ (M2 × N),
(M1 ∪ M2 ) × N = (M1 × N) ∪ (M2 × N).
Sofort einsichtig ist: Hat M genau m Elemente und N genau n
Elemente, so hat M × N genau m · n Elemente.
§1 Elementare Logik und Mengenlehre
Das kartesische Produkt zweier Mengen M, N ist die Menge
M × N := {(x, y ) : x ∈ M, y ∈ N}.
Hierfür gelten:
(M1 ∩ M2 ) × N = (M1 × N) ∩ (M2 × N),
(M1 ∪ M2 ) × N = (M1 × N) ∪ (M2 × N).
Sofort einsichtig ist: Hat M genau m Elemente und N genau n
Elemente, so hat M × N genau m · n Elemente.
§1 Elementare Logik und Mengenlehre
Das kartesische Produkt zweier Mengen M, N ist die Menge
M × N := {(x, y ) : x ∈ M, y ∈ N}.
Hierfür gelten:
(M1 ∩ M2 ) × N = (M1 × N) ∩ (M2 × N),
(M1 ∪ M2 ) × N = (M1 × N) ∪ (M2 × N).
Sofort einsichtig ist: Hat M genau m Elemente und N genau n
Elemente, so hat M × N genau m · n Elemente.
§1 Elementare Logik und Mengenlehre
Der harmlos anmutende Begriff der Menge hat seine Tücken. Der
Logiker Bertrand Russel erdachte sich 1902 folgendes Beispiel: Sei
M die Menge aller Mengen, die sich selbst nicht enthalten. Die so
genannte Russelsche Antinomie fragt nun, ob M sich selbst enthält
oder nicht?
Diese Frage ist unmöglich zu beantworten und erinnert an das
Paradoxon des Barbiers, der jeden Einwohner seines Ortes rasiert,
der sich nicht selbst rasiert. Diese widersprüchlichen Aussagen
ähneln dem selbstbezüglichen Satz:
Dieser Satz ist falsch.
In diesem Zusammenhang sei noch an den Kreter Epimenides
erinnert, der da sagte, dass alle Kreter lügen.
§1 Elementare Logik und Mengenlehre
Der harmlos anmutende Begriff der Menge hat seine Tücken. Der
Logiker Bertrand Russel erdachte sich 1902 folgendes Beispiel: Sei
M die Menge aller Mengen, die sich selbst nicht enthalten. Die so
genannte Russelsche Antinomie fragt nun, ob M sich selbst enthält
oder nicht?
Diese Frage ist unmöglich zu beantworten und erinnert an das
Paradoxon des Barbiers, der jeden Einwohner seines Ortes rasiert,
der sich nicht selbst rasiert. Diese widersprüchlichen Aussagen
ähneln dem selbstbezüglichen Satz:
Dieser Satz ist falsch.
In diesem Zusammenhang sei noch an den Kreter Epimenides
erinnert, der da sagte, dass alle Kreter lügen.
Resümee
Mathematik betseht aus einer Vielzahl von verschiedenen Diziplinen
(wie z.B. Mengenlehre). Jede solche basiert auf Aussagen, welche
als wahr angesehen werden, den so genannten Axiomen; aus diesen
werden dann weitere wahre Aussagen hergeleitet, jeweils in Form
eines Satzes. Dabei geschieht diese Herleitung nach genau
festgelegten Schlussregeln, dem Beweis des Satzes; ein Axiom
hingegen wird nicht bewiesen, sonst wäre es ein Satz.
Die Weiterentwicklung der Mathematik geschieht oft durch
Sammlungen von Sätzen, Beweisen und Definitionen, die nicht
unbedingt axiomatisch strukturiert sind, sondern vor allem durch
die Intuition und Erfahrung der Beteiligten geprägt sind.
Resümee
Mathematik betseht aus einer Vielzahl von verschiedenen Diziplinen
(wie z.B. Mengenlehre). Jede solche basiert auf Aussagen, welche
als wahr angesehen werden, den so genannten Axiomen; aus diesen
werden dann weitere wahre Aussagen hergeleitet, jeweils in Form
eines Satzes. Dabei geschieht diese Herleitung nach genau
festgelegten Schlussregeln, dem Beweis des Satzes; ein Axiom
hingegen wird nicht bewiesen, sonst wäre es ein Satz.
Die Weiterentwicklung der Mathematik geschieht oft durch
Sammlungen von Sätzen, Beweisen und Definitionen, die nicht
unbedingt axiomatisch strukturiert sind, sondern vor allem durch
die Intuition und Erfahrung der Beteiligten geprägt sind.
§2 Die natürlichen Zahlen und das
Induktionsprinzip
”Zehen sind figurn/darmit ein jede zal geschrieben wirt/sind also
gestalt. 1.2.3.4.5.6.7.8.9.0. Die ersten neun bedeuten/die zehent als
0 gibt in fursetzung mehr bedeutung/gilt aber allein nichts/ wie hie
10.20.30...” schreibt Adam Ries im 16. Jahrhundert.
In seiner berühmten berühmten Annaberger Brotordnung wird
erklärt, wie sich das Gewicht eines Brotes unter Beibehaltung des
Getreidepreises ändert. Ries hierzu, dass ”der arme gemeine man ym
Brotkauff nicht übersetzt würde” (also nicht betrogen würde). Das
Wort ’kleine Brötchen backen’ hat in dieser Zeit seinen Ursprung!
§2 Die natürlichen Zahlen und das
Induktionsprinzip
”Zehen sind figurn/darmit ein jede zal geschrieben wirt/sind also
gestalt. 1.2.3.4.5.6.7.8.9.0. Die ersten neun bedeuten/die zehent als
0 gibt in fursetzung mehr bedeutung/gilt aber allein nichts/ wie hie
10.20.30...” schreibt Adam Ries im 16. Jahrhundert.
In seiner berühmten berühmten Annaberger Brotordnung wird
erklärt, wie sich das Gewicht eines Brotes unter Beibehaltung des
Getreidepreises ändert. Ries hierzu, dass ”der arme gemeine man ym
Brotkauff nicht übersetzt würde” (also nicht betrogen würde). Das
Wort ’kleine Brötchen backen’ hat in dieser Zeit seinen Ursprung!
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Die natürlichen Zahlen kommen vom Zählen, und genau dieser
Zählprozess wird durch die Peano-Axiome formalisiert: Es sei N eine
Menge mit einem Element 1 ∈ N, und es existiert eine
’Nachfolgerfunktion’ f : N → N mit folgenden Eigenschaften:
Es gibt kein Element n ∈ N mit Nachfolger 1 = f (n);
sind m, n ∈ N verschieden, so sind auch deren Nachfolger
verschieden (bzw. f (m) = f (n) ⇒ m = n);
jede Teilmenge von N, die 1 enthält und mit jedem n ∈ N auch
dessen Nachfolger f (n), ist bereits die gesamte Menge N.
Die Elemente der Menge N heißen natürliche Zahlen. Es gibt derer
unendlich viele...
Die Nachfolgerfunktion induziert eine Anordnung der Elemente von
N, nämlich 1, f (1), f (f (1)), f (f (f (1))), . . ., welche wir
üblicherweise als 1, 2, 3, 4, , . . . notieren. Wir schreiben z.B.
2 < 3 und sagen 2 ist kleiner 3.
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Die natürlichen Zahlen kommen vom Zählen, und genau dieser
Zählprozess wird durch die Peano-Axiome formalisiert: Es sei N eine
Menge mit einem Element 1 ∈ N, und es existiert eine
’Nachfolgerfunktion’ f : N → N mit folgenden Eigenschaften:
Es gibt kein Element n ∈ N mit Nachfolger 1 = f (n);
sind m, n ∈ N verschieden, so sind auch deren Nachfolger
verschieden (bzw. f (m) = f (n) ⇒ m = n);
jede Teilmenge von N, die 1 enthält und mit jedem n ∈ N auch
dessen Nachfolger f (n), ist bereits die gesamte Menge N.
Die Elemente der Menge N heißen natürliche Zahlen. Es gibt derer
unendlich viele...
Die Nachfolgerfunktion induziert eine Anordnung der Elemente von
N, nämlich 1, f (1), f (f (1)), f (f (f (1))), . . ., welche wir
üblicherweise als 1, 2, 3, 4, , . . . notieren. Wir schreiben z.B.
2 < 3 und sagen 2 ist kleiner 3.
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Die natürlichen Zahlen kommen vom Zählen, und genau dieser
Zählprozess wird durch die Peano-Axiome formalisiert: Es sei N eine
Menge mit einem Element 1 ∈ N, und es existiert eine
’Nachfolgerfunktion’ f : N → N mit folgenden Eigenschaften:
Es gibt kein Element n ∈ N mit Nachfolger 1 = f (n);
sind m, n ∈ N verschieden, so sind auch deren Nachfolger
verschieden (bzw. f (m) = f (n) ⇒ m = n);
jede Teilmenge von N, die 1 enthält und mit jedem n ∈ N auch
dessen Nachfolger f (n), ist bereits die gesamte Menge N.
Die Elemente der Menge N heißen natürliche Zahlen. Es gibt derer
unendlich viele...
Die Nachfolgerfunktion induziert eine Anordnung der Elemente von
N, nämlich 1, f (1), f (f (1)), f (f (f (1))), . . ., welche wir
üblicherweise als 1, 2, 3, 4, , . . . notieren. Wir schreiben z.B.
2 < 3 und sagen 2 ist kleiner 3.
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Die natürlichen Zahlen kommen vom Zählen, und genau dieser
Zählprozess wird durch die Peano-Axiome formalisiert: Es sei N eine
Menge mit einem Element 1 ∈ N, und es existiert eine
’Nachfolgerfunktion’ f : N → N mit folgenden Eigenschaften:
Es gibt kein Element n ∈ N mit Nachfolger 1 = f (n);
sind m, n ∈ N verschieden, so sind auch deren Nachfolger
verschieden (bzw. f (m) = f (n) ⇒ m = n);
jede Teilmenge von N, die 1 enthält und mit jedem n ∈ N auch
dessen Nachfolger f (n), ist bereits die gesamte Menge N.
Die Elemente der Menge N heißen natürliche Zahlen. Es gibt derer
unendlich viele...
Die Nachfolgerfunktion induziert eine Anordnung der Elemente von
N, nämlich 1, f (1), f (f (1)), f (f (f (1))), . . ., welche wir
üblicherweise als 1, 2, 3, 4, , . . . notieren. Wir schreiben z.B.
2 < 3 und sagen 2 ist kleiner 3.
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Die natürlichen Zahlen kommen vom Zählen, und genau dieser
Zählprozess wird durch die Peano-Axiome formalisiert: Es sei N eine
Menge mit einem Element 1 ∈ N, und es existiert eine
’Nachfolgerfunktion’ f : N → N mit folgenden Eigenschaften:
Es gibt kein Element n ∈ N mit Nachfolger 1 = f (n);
sind m, n ∈ N verschieden, so sind auch deren Nachfolger
verschieden (bzw. f (m) = f (n) ⇒ m = n);
jede Teilmenge von N, die 1 enthält und mit jedem n ∈ N auch
dessen Nachfolger f (n), ist bereits die gesamte Menge N.
Die Elemente der Menge N heißen natürliche Zahlen. Es gibt derer
unendlich viele...
Die Nachfolgerfunktion induziert eine Anordnung der Elemente von
N, nämlich 1, f (1), f (f (1)), f (f (f (1))), . . ., welche wir
üblicherweise als 1, 2, 3, 4, , . . . notieren. Wir schreiben z.B.
2 < 3 und sagen 2 ist kleiner 3.
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Die natürlichen Zahlen kommen vom Zählen, und genau dieser
Zählprozess wird durch die Peano-Axiome formalisiert: Es sei N eine
Menge mit einem Element 1 ∈ N, und es existiert eine
’Nachfolgerfunktion’ f : N → N mit folgenden Eigenschaften:
Es gibt kein Element n ∈ N mit Nachfolger 1 = f (n);
sind m, n ∈ N verschieden, so sind auch deren Nachfolger
verschieden (bzw. f (m) = f (n) ⇒ m = n);
jede Teilmenge von N, die 1 enthält und mit jedem n ∈ N auch
dessen Nachfolger f (n), ist bereits die gesamte Menge N.
Die Elemente der Menge N heißen natürliche Zahlen. Es gibt derer
unendlich viele...
Die Nachfolgerfunktion induziert eine Anordnung der Elemente von
N, nämlich 1, f (1), f (f (1)), f (f (f (1))), . . ., welche wir
üblicherweise als 1, 2, 3, 4, , . . . notieren. Wir schreiben z.B.
2 < 3 und sagen 2 ist kleiner 3.
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Die natürlichen Zahlen kommen vom Zählen, und genau dieser
Zählprozess wird durch die Peano-Axiome formalisiert: Es sei N eine
Menge mit einem Element 1 ∈ N, und es existiert eine
’Nachfolgerfunktion’ f : N → N mit folgenden Eigenschaften:
Es gibt kein Element n ∈ N mit Nachfolger 1 = f (n);
sind m, n ∈ N verschieden, so sind auch deren Nachfolger
verschieden (bzw. f (m) = f (n) ⇒ m = n);
jede Teilmenge von N, die 1 enthält und mit jedem n ∈ N auch
dessen Nachfolger f (n), ist bereits die gesamte Menge N.
Die Elemente der Menge N heißen natürliche Zahlen. Es gibt derer
unendlich viele...
Die Nachfolgerfunktion induziert eine Anordnung der Elemente von
N, nämlich 1, f (1), f (f (1)), f (f (f (1))), . . ., welche wir
üblicherweise als 1, 2, 3, 4, , . . . notieren. Wir schreiben z.B.
2 < 3 und sagen 2 ist kleiner 3.
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Die Addition zweier natürlicher Zahlen definieren wir rekursiv durch
n+1 := f (n)
und
n+f (m) := f (n+m)
für alle m, n ∈ N.
Die Festlegung der Nachfolgerfunktion als n 7→ f (n) = n + 1 liefert
unter Zuhilfenahme des ersten Axioms alle uns vertrauten
natürlichen Zahlen sukzessive aus dem ausgezeichneten Element
1 ∈ N als Nachfolger bzw. Nachfolger des Nachfolgers usw.:
1 ∈ N → 2 = 1+1 = f (1) ∈ N → . . . → n ∈ N → n+1 = f (n) ∈ N → . . .
Die Multiplikation ist erklärt durch
n · 1 := n
und
n · f (m) := n · m + n
für alle m, n ∈ N.
Sowohl Addition als auch die Multiplikation sind kommutativ, d.h.
stets gilt
m+n =n+m
und
m · n = n · m.
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Die Addition zweier natürlicher Zahlen definieren wir rekursiv durch
n+1 := f (n)
und
n+f (m) := f (n+m)
für alle m, n ∈ N.
Die Festlegung der Nachfolgerfunktion als n 7→ f (n) = n + 1 liefert
unter Zuhilfenahme des ersten Axioms alle uns vertrauten
natürlichen Zahlen sukzessive aus dem ausgezeichneten Element
1 ∈ N als Nachfolger bzw. Nachfolger des Nachfolgers usw.:
1 ∈ N → 2 = 1+1 = f (1) ∈ N → . . . → n ∈ N → n+1 = f (n) ∈ N → . . .
Die Multiplikation ist erklärt durch
n · 1 := n
und
n · f (m) := n · m + n
für alle m, n ∈ N.
Sowohl Addition als auch die Multiplikation sind kommutativ, d.h.
stets gilt
m+n =n+m
und
m · n = n · m.
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Die Addition zweier natürlicher Zahlen definieren wir rekursiv durch
n+1 := f (n)
und
n+f (m) := f (n+m)
für alle m, n ∈ N.
Die Festlegung der Nachfolgerfunktion als n 7→ f (n) = n + 1 liefert
unter Zuhilfenahme des ersten Axioms alle uns vertrauten
natürlichen Zahlen sukzessive aus dem ausgezeichneten Element
1 ∈ N als Nachfolger bzw. Nachfolger des Nachfolgers usw.:
1 ∈ N → 2 = 1+1 = f (1) ∈ N → . . . → n ∈ N → n+1 = f (n) ∈ N → . . .
Die Multiplikation ist erklärt durch
n · 1 := n
und
n · f (m) := n · m + n
für alle m, n ∈ N.
Sowohl Addition als auch die Multiplikation sind kommutativ, d.h.
stets gilt
m+n =n+m
und
m · n = n · m.
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Das letzte der Peano-Axiome ist von besonderer Bedeutung,
insbesondere als Beweismethode. Etwas anschaulicher formuliert
sich dieses wie folgt:
Prinzip der vollständigen Induktion: Wenn eine Eigenschaft E auf 1
zutrifft und aus der Gültigkeit von E für n ∈ N stets die Gültigkeit
von E für den Nachfolger n + 1 folgt, dann ist die Aussage E für
alle Elemente von N wahr.
Sei
N := {n ∈ N : E(n) ist wahr},
dann genügt es die Gültigkeit von E(1) sowie die Implikation
E(n) ⇒ E(n + 1) für alle n ∈ N nachzuweisen, weil damit
E(1) ⇒ E(2) ⇒ . . . ⇒ E(n) ⇒ E(n + 1) ⇒ . . .
nach dem Prinzip der vollständigen Induktion nun N = N folgt.
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Das letzte der Peano-Axiome ist von besonderer Bedeutung,
insbesondere als Beweismethode. Etwas anschaulicher formuliert
sich dieses wie folgt:
Prinzip der vollständigen Induktion: Wenn eine Eigenschaft E auf 1
zutrifft und aus der Gültigkeit von E für n ∈ N stets die Gültigkeit
von E für den Nachfolger n + 1 folgt, dann ist die Aussage E für
alle Elemente von N wahr.
Sei
N := {n ∈ N : E(n) ist wahr},
dann genügt es die Gültigkeit von E(1) sowie die Implikation
E(n) ⇒ E(n + 1) für alle n ∈ N nachzuweisen, weil damit
E(1) ⇒ E(2) ⇒ . . . ⇒ E(n) ⇒ E(n + 1) ⇒ . . .
nach dem Prinzip der vollständigen Induktion nun N = N folgt.
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Vor dem ersten Beispiel führen wir eine abkürzende Schreibweise für
Summen und Produkte ein:
n
X
aj := a1 + a2 + . . . + an
j=1
und
n
Y
j=1
aj := a1 · a2 · . . . · an .
Wir könnten diese Symbole für die Summe auch per Induktion
erklären, z.B.:
1
X
j=1
aj := a1
und
n+1
X
j=1
aj := an+1 +
n
X
j=1
aj .
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Vor dem ersten Beispiel führen wir eine abkürzende Schreibweise für
Summen und Produkte ein:
n
X
aj := a1 + a2 + . . . + an
j=1
und
n
Y
j=1
aj := a1 · a2 · . . . · an .
Wir könnten diese Symbole für die Summe auch per Induktion
erklären, z.B.:
1
X
j=1
aj := a1
und
n+1
X
j=1
aj := an+1 +
n
X
j=1
aj .
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Die Bezeichnung des ganzzahligen Index – hier der Buchstabe ’j ’ –
ist dabei nicht von Bedeutung (wie man der Definition entnimmt),
wohl aber die Grenzen für den Bereich dieses Indizes, die unterbzw. oberhalb des jeweiligen Symbols angebracht sind.
Summen oder Produkte müssen natürlich nicht notwendig mit dem
Index 1 anfangen. Ferner erklären wir die leere Summe bzw. das
leere Produkt durch
0
X
j=1
aj := 0
bzw.
0
Y
j=1
aj := 1,
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Die Bezeichnung des ganzzahligen Index – hier der Buchstabe ’j ’ –
ist dabei nicht von Bedeutung (wie man der Definition entnimmt),
wohl aber die Grenzen für den Bereich dieses Indizes, die unterbzw. oberhalb des jeweiligen Symbols angebracht sind.
Summen oder Produkte müssen natürlich nicht notwendig mit dem
Index 1 anfangen. Ferner erklären wir die leere Summe bzw. das
leere Produkt durch
0
X
j=1
aj := 0
bzw.
0
Y
j=1
aj := 1,
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Erste Beispiele für Aussagen, die wir mit Induktion beweisen
können:
Satz 2.1 Für alle n ∈ N gelten
n
X
k = 21 n(n + 1).
k=1
und
n
X
k=1
(2k − 1) = n2 .
Was hat das mit dem folgenden Bild zu tun?
•
• △
△ △
• △ ⋆
△ △ ⋆
⋆ ⋆ ⋆
...
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Und noch ein Beispiel für einen Induktionsbeweis liefert
Satz 2.2 [Formel für die endliche geometrische Reihe]
Für x 6= 1 und n ∈ N0 gilt
n
X
k=0
xk =
1 − x n+1
;
1−x
für x = 1 besitzt die Reihe den Wert n + 1.
Die auftretende Summe heißt endliche geometrische Reihe.
Beispielsweise zeigt sich so 1 + 2 + 22 + 23 + 29 = 210 − 1.
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Berechnung einer unendlichen geometrischen Reihe ohne Worte!
(nach Rick Mabry)
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Äquivalent zum Induktionsprinzip ist die Wohlordnung von N:
Satz 2.3 [Wohlordnung]
Jede nicht-leere Teilmenge M ⊂ N besitzt ein kleinstes Element.
Die Nachfolgerfunktion impliziert nämlich eine Anordnung der
natürlichen Zahlen. Deshalb sagt man auch, die natürlichen Zahlen
seien wohlgeordnet.
Die Aussage gilt übrigens weder für die Menge der ganzen noch für
die Menge der rationalen Zahlen aus offensichtlichen Gründen).
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Äquivalent zum Induktionsprinzip ist die Wohlordnung von N:
Satz 2.3 [Wohlordnung]
Jede nicht-leere Teilmenge M ⊂ N besitzt ein kleinstes Element.
Die Nachfolgerfunktion impliziert nämlich eine Anordnung der
natürlichen Zahlen. Deshalb sagt man auch, die natürlichen Zahlen
seien wohlgeordnet.
Die Aussage gilt übrigens weder für die Menge der ganzen noch für
die Menge der rationalen Zahlen aus offensichtlichen Gründen).
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Für eine natürliche Zahl n ist die Fakultät erklärt durch
n
Y
n! =
sowie
0! = 1;
k=1
wir sagen für n! einfach „n Fakultät“.
Die Fakultät n! wächst rasant mit n:
6! = 720,
16! = 20 922 789 888 000,
26! = 403 291 461 126 605 635 584 000 000,
36! = 371 993 326 789 901 217 467 999 448 150 835 200 000 000.
Aufgabe: Finde m, n ∈ N, so dass
m! < 10100 < (m + 1)!
und
2n < 10100 < 2n+1 .
Ohne Computereinsatz ist dies keine leichte Aufgabe!
§2 Die natürlichen Zahlen und das
Induktionsprinzip
Für eine natürliche Zahl n ist die Fakultät erklärt durch
n
Y
n! =
sowie
0! = 1;
k=1
wir sagen für n! einfach „n Fakultät“.
Die Fakultät n! wächst rasant mit n:
6! = 720,
16! = 20 922 789 888 000,
26! = 403 291 461 126 605 635 584 000 000,
36! = 371 993 326 789 901 217 467 999 448 150 835 200 000 000.
Aufgabe: Finde m, n ∈ N, so dass
m! < 10100 < (m + 1)!
und
2n < 10100 < 2n+1 .
Ohne Computereinsatz ist dies keine leichte Aufgabe!
Resümee
Die Menge der natürlichen Zahlen
N = {1, 2, 3, . . .}
wurde axiomatisch eingeführt; sie besitzt unendlich viele Elemente
und ist wohlgeordnet. Die Null ist (bei uns) keine natürliche Zahl!
Addition und Multiplikation natürlicher Zahlen wurden definiert;
diese stimmen mit den uns aus der Schule vertrauten
Rechenoperationen überein.
Das Prinzip der vollständigen Induktion ist ein wichtiges
Beweisverfahren, und liefert beispielsweise einen geschlossenen
Ausdruck für die endliche geometrische Reihe.
Resümee
Die Menge der natürlichen Zahlen
N = {1, 2, 3, . . .}
wurde axiomatisch eingeführt; sie besitzt unendlich viele Elemente
und ist wohlgeordnet. Die Null ist (bei uns) keine natürliche Zahl!
Addition und Multiplikation natürlicher Zahlen wurden definiert;
diese stimmen mit den uns aus der Schule vertrauten
Rechenoperationen überein.
Das Prinzip der vollständigen Induktion ist ein wichtiges
Beweisverfahren, und liefert beispielsweise einen geschlossenen
Ausdruck für die endliche geometrische Reihe.
§3 Die ganzen und die rationalen Zahlen
Die Menge Z der ganzen Zahlen entsteht aus N durch Hinzunahme
der Null als bzgl. der Addition neutralem Element, sowie der additiv
Inversen −n zu jedem n ∈ N:
Z = {0, 1, −1, 2, −2, , . . . , n, −n, . . .}
Durch Übergang zu dem Quotienten Q, der Menge der rationalen
Zahlen bestehend aus den Brüchen ba mit a ∈ Z und b ∈ N, erhält
man eine Obermenge, die auch die multiplikativen Inversen der
Zahlen ungleich null enthält:
o
na
: a ∈ Z, b ∈ N
Q=
b
Insbesondere kann in Q jede lineare Gleichung mit Koeffizienten in
Z bzw. Q gelöst werden.
§3 Die ganzen und die rationalen Zahlen
Die Menge Z der ganzen Zahlen entsteht aus N durch Hinzunahme
der Null als bzgl. der Addition neutralem Element, sowie der additiv
Inversen −n zu jedem n ∈ N:
Z = {0, 1, −1, 2, −2, , . . . , n, −n, . . .}
Durch Übergang zu dem Quotienten Q, der Menge der rationalen
Zahlen bestehend aus den Brüchen ba mit a ∈ Z und b ∈ N, erhält
man eine Obermenge, die auch die multiplikativen Inversen der
Zahlen ungleich null enthält:
o
na
: a ∈ Z, b ∈ N
Q=
b
Insbesondere kann in Q jede lineare Gleichung mit Koeffizienten in
Z bzw. Q gelöst werden.
§3 Die ganzen und die rationalen Zahlen
Die Menge Z der ganzen Zahlen entsteht aus N durch Hinzunahme
der Null als bzgl. der Addition neutralem Element, sowie der additiv
Inversen −n zu jedem n ∈ N:
Z = {0, 1, −1, 2, −2, , . . . , n, −n, . . .}
Durch Übergang zu dem Quotienten Q, der Menge der rationalen
Zahlen bestehend aus den Brüchen ba mit a ∈ Z und b ∈ N, erhält
man eine Obermenge, die auch die multiplikativen Inversen der
Zahlen ungleich null enthält:
o
na
: a ∈ Z, b ∈ N
Q=
b
Insbesondere kann in Q jede lineare Gleichung mit Koeffizienten in
Z bzw. Q gelöst werden.
§3 Die ganzen und die rationalen Zahlen
Gegeben eine Menge M, dann ist eine Relation auf M eine
Teilmenge R ⊂ M × M; wir notieren:
x ∼R y
:⇔
(x, y ) ∈ R;
wenn aus dem Kontext klar ist, welche Relation R zu Grunde liegt,
so schreiben wir auch nur x ∼ y .
Mit der Kleiner-Relation ’<’ kennen wir ein bereits ein Beispiel.
Eine Relation auf M heißt Äquivalenzrelation, wenn gilt:
Reflexivität: x ∼ x ;
Symmetrie: x ∼ y ⇒ y ∼ x;
Transitivität: x ∼ y , y ∼ z ⇒ x ∼ z.
Wir lesen x ∼ y bzw. x ∼R y als „x ist äquivalent zu y bzgl. R“.
§3 Die ganzen und die rationalen Zahlen
Gegeben eine Menge M, dann ist eine Relation auf M eine
Teilmenge R ⊂ M × M; wir notieren:
x ∼R y
:⇔
(x, y ) ∈ R;
wenn aus dem Kontext klar ist, welche Relation R zu Grunde liegt,
so schreiben wir auch nur x ∼ y .
Mit der Kleiner-Relation ’<’ kennen wir ein bereits ein Beispiel.
Eine Relation auf M heißt Äquivalenzrelation, wenn gilt:
Reflexivität: x ∼ x ;
Symmetrie: x ∼ y ⇒ y ∼ x;
Transitivität: x ∼ y , y ∼ z ⇒ x ∼ z.
Wir lesen x ∼ y bzw. x ∼R y als „x ist äquivalent zu y bzgl. R“.
§3 Die ganzen und die rationalen Zahlen
Gegeben eine Menge M, dann ist eine Relation auf M eine
Teilmenge R ⊂ M × M; wir notieren:
x ∼R y
:⇔
(x, y ) ∈ R;
wenn aus dem Kontext klar ist, welche Relation R zu Grunde liegt,
so schreiben wir auch nur x ∼ y .
Mit der Kleiner-Relation ’<’ kennen wir ein bereits ein Beispiel.
Eine Relation auf M heißt Äquivalenzrelation, wenn gilt:
Reflexivität: x ∼ x ;
Symmetrie: x ∼ y ⇒ y ∼ x;
Transitivität: x ∼ y , y ∼ z ⇒ x ∼ z.
Wir lesen x ∼ y bzw. x ∼R y als „x ist äquivalent zu y bzgl. R“.
§3 Die ganzen und die rationalen Zahlen
Jede Äquivalenzrelation ∼ auf einer Menge M induziert eine
Zerlegung von M in disjunkte Teilmengen. Dabei ist für jedes
Element x ∈ M die Äquivalenzklasse von x bezüglich R definiert als
die Teilmenge
Kl(x) := {y ∈ M : x ∼ y }.
Satz 3.1 Für eine Äquivalenzrelation R ⊂ M × M gelten:
1
2
3
x ∈ Kl(x);
x ∼ y ⇔ Kl(x) = Kl(y );
Kl(x) 6= Kl(y ) ⇔ Kl(x) ∩ Kl(y ) = ∅.
§3 Die ganzen und die rationalen Zahlen
Jede Äquivalenzrelation ∼ auf einer Menge M induziert eine
Zerlegung von M in disjunkte Teilmengen. Dabei ist für jedes
Element x ∈ M die Äquivalenzklasse von x bezüglich R definiert als
die Teilmenge
Kl(x) := {y ∈ M : x ∼ y }.
Satz 3.1 Für eine Äquivalenzrelation R ⊂ M × M gelten:
1
2
3
x ∈ Kl(x);
x ∼ y ⇔ Kl(x) = Kl(y );
Kl(x) 6= Kl(y ) ⇔ Kl(x) ∩ Kl(y ) = ∅.
§3 Die ganzen und die rationalen Zahlen
Jede Äquivalenzrelation ∼ auf einer Menge M induziert eine
Zerlegung von M in disjunkte Teilmengen. Dabei ist für jedes
Element x ∈ M die Äquivalenzklasse von x bezüglich R definiert als
die Teilmenge
Kl(x) := {y ∈ M : x ∼ y }.
Satz 3.1 Für eine Äquivalenzrelation R ⊂ M × M gelten:
1
2
3
x ∈ Kl(x);
x ∼ y ⇔ Kl(x) = Kl(y );
Kl(x) 6= Kl(y ) ⇔ Kl(x) ∩ Kl(y ) = ∅.
§3 Die ganzen und die rationalen Zahlen
Jede Äquivalenzrelation ∼ auf einer Menge M induziert eine
Zerlegung von M in disjunkte Teilmengen. Dabei ist für jedes
Element x ∈ M die Äquivalenzklasse von x bezüglich R definiert als
die Teilmenge
Kl(x) := {y ∈ M : x ∼ y }.
Satz 3.1 Für eine Äquivalenzrelation R ⊂ M × M gelten:
1
2
3
x ∈ Kl(x);
x ∼ y ⇔ Kl(x) = Kl(y );
Kl(x) 6= Kl(y ) ⇔ Kl(x) ∩ Kl(y ) = ∅.
§3 Die ganzen und die rationalen Zahlen
Ein weiteres wichtiges Beispiel liefert die Gleichheitsrelation ’=’.
Die Gleichheit natürlicher Zahlen ist eine Äquivalenzrelation auf N
gegeben durch die Relation
R = {(m, n) ∈ N × N : m = n};
die Verifizierung ist trivial. Die Äquivalenzklassen sind hierbei
allesamt ein-elementig: Kl(x) = {x}.
Hingegen definiert die Kleiner/Gleich-Relation ’≤’ zwar eine
Relation, aber keine Äquivalenzrelation, denn die Symmetrie ist i.A.
nicht gewährleistet, da ja z.B. 3 ≤ 7, aber die Umkehrung gilt
sicherlich nicht.
Sei M eine endliche Menge und 2M die zugehörige Potenzmenge.
Eine Äquivalenzrelation auf 2M ist gegeben durch
A∼B
: ⇐⇒
A und B haben dieselbe Anzahl von Elementen.
§3 Die ganzen und die rationalen Zahlen
Ein weiteres wichtiges Beispiel liefert die Gleichheitsrelation ’=’.
Die Gleichheit natürlicher Zahlen ist eine Äquivalenzrelation auf N
gegeben durch die Relation
R = {(m, n) ∈ N × N : m = n};
die Verifizierung ist trivial. Die Äquivalenzklassen sind hierbei
allesamt ein-elementig: Kl(x) = {x}.
Hingegen definiert die Kleiner/Gleich-Relation ’≤’ zwar eine
Relation, aber keine Äquivalenzrelation, denn die Symmetrie ist i.A.
nicht gewährleistet, da ja z.B. 3 ≤ 7, aber die Umkehrung gilt
sicherlich nicht.
Sei M eine endliche Menge und 2M die zugehörige Potenzmenge.
Eine Äquivalenzrelation auf 2M ist gegeben durch
A∼B
: ⇐⇒
A und B haben dieselbe Anzahl von Elementen.
§3 Die ganzen und die rationalen Zahlen
Ein weiteres wichtiges Beispiel liefert die Gleichheitsrelation ’=’.
Die Gleichheit natürlicher Zahlen ist eine Äquivalenzrelation auf N
gegeben durch die Relation
R = {(m, n) ∈ N × N : m = n};
die Verifizierung ist trivial. Die Äquivalenzklassen sind hierbei
allesamt ein-elementig: Kl(x) = {x}.
Hingegen definiert die Kleiner/Gleich-Relation ’≤’ zwar eine
Relation, aber keine Äquivalenzrelation, denn die Symmetrie ist i.A.
nicht gewährleistet, da ja z.B. 3 ≤ 7, aber die Umkehrung gilt
sicherlich nicht.
Sei M eine endliche Menge und 2M die zugehörige Potenzmenge.
Eine Äquivalenzrelation auf 2M ist gegeben durch
A∼B
: ⇐⇒
A und B haben dieselbe Anzahl von Elementen.
§3 Die ganzen und die rationalen Zahlen
Nun konstruieren wir die Menge Z der ganzen Zahlen formal
korrekt aus der Menge N der natürlichen Zahlen heraus:
Wir betrachten geordnete Paare (a, b) ∈ N2 := N × N, wobei
geordnet hier bedeutet, dass genau dann (a, b) = (c, d ) gilt, wenn
a = c und b = d . Nun identifizieren wir Paare, welche die gleiche
Differenz besitzen (wie etwa (5, 3) und (12, 10)) mittels der
Äquivalenzrelation
(a, b) ∼ (m, n)
: ⇐⇒
a + n = b + m.
Wir bezeichnen die Äquivalenzklassen kurz mit [a, b] und nennen
eine jede solche eine ganze Zahl; und Z sei deren Gesamtheit.
Wir finden die uns bekannten natürlichen Zahlen als Teilmenge
wieder:
N⊂Z
vermöge
ϕ : N → Z, n 7→ [n + 1, 1].
§3 Die ganzen und die rationalen Zahlen
Nun konstruieren wir die Menge Z der ganzen Zahlen formal
korrekt aus der Menge N der natürlichen Zahlen heraus:
Wir betrachten geordnete Paare (a, b) ∈ N2 := N × N, wobei
geordnet hier bedeutet, dass genau dann (a, b) = (c, d ) gilt, wenn
a = c und b = d . Nun identifizieren wir Paare, welche die gleiche
Differenz besitzen (wie etwa (5, 3) und (12, 10)) mittels der
Äquivalenzrelation
(a, b) ∼ (m, n)
: ⇐⇒
a + n = b + m.
Wir bezeichnen die Äquivalenzklassen kurz mit [a, b] und nennen
eine jede solche eine ganze Zahl; und Z sei deren Gesamtheit.
Wir finden die uns bekannten natürlichen Zahlen als Teilmenge
wieder:
N⊂Z
vermöge
ϕ : N → Z, n 7→ [n + 1, 1].
§3 Die ganzen und die rationalen Zahlen
Nun konstruieren wir die Menge Z der ganzen Zahlen formal
korrekt aus der Menge N der natürlichen Zahlen heraus:
Wir betrachten geordnete Paare (a, b) ∈ N2 := N × N, wobei
geordnet hier bedeutet, dass genau dann (a, b) = (c, d ) gilt, wenn
a = c und b = d . Nun identifizieren wir Paare, welche die gleiche
Differenz besitzen (wie etwa (5, 3) und (12, 10)) mittels der
Äquivalenzrelation
(a, b) ∼ (m, n)
: ⇐⇒
a + n = b + m.
Wir bezeichnen die Äquivalenzklassen kurz mit [a, b] und nennen
eine jede solche eine ganze Zahl; und Z sei deren Gesamtheit.
Wir finden die uns bekannten natürlichen Zahlen als Teilmenge
wieder:
N⊂Z
vermöge
ϕ : N → Z, n 7→ [n + 1, 1].
§3 Die ganzen und die rationalen Zahlen
Wir erklären eine Addition in Z durch
[a, b] + [c, d ] := [a + c, b + d ];
man beachte, dass hier die Addition links in natürlicher Weise durch
die in N (rechts) definiert ist.
Analog definieren wir eine Multiplikation durch
[a, b] · [c, d ] := [ac + bd , bc + ad ].
Diese Vorschriften sind wohldefiniert, d.h. unabhängig von den
gewählten Repräsentanten, und kompatibel mit denen aus N.
§3 Die ganzen und die rationalen Zahlen
Wir erklären eine Addition in Z durch
[a, b] + [c, d ] := [a + c, b + d ];
man beachte, dass hier die Addition links in natürlicher Weise durch
die in N (rechts) definiert ist.
Analog definieren wir eine Multiplikation durch
[a, b] · [c, d ] := [ac + bd , bc + ad ].
Diese Vorschriften sind wohldefiniert, d.h. unabhängig von den
gewählten Repräsentanten, und kompatibel mit denen aus N.
§3 Die ganzen und die rationalen Zahlen
Wir erklären eine Addition in Z durch
[a, b] + [c, d ] := [a + c, b + d ];
man beachte, dass hier die Addition links in natürlicher Weise durch
die in N (rechts) definiert ist.
Analog definieren wir eine Multiplikation durch
[a, b] · [c, d ] := [ac + bd , bc + ad ].
Diese Vorschriften sind wohldefiniert, d.h. unabhängig von den
gewählten Repräsentanten, und kompatibel mit denen aus N.
§3 Die ganzen und die rationalen Zahlen
Die Null ’0’ tritt dabei als die Äquivalenzklasse [k, k] mit einer
beliebigen natürlichen Zahl k auf und das additiv Inverse
−[n + 1, 1] einer beliebigen, aber festen natürlichen Zahl
n = [n + 1, 1] erklärt sich als [1, n + 1].
Zur Vereinfachung ersetzen wir die Äquivalenzklassenschreibweise
im Folgenden durch unsere übliche Notation ganzer Zahlen.
Es gelten die üblichen (und wichtigen) Rechengesetze, nämlich
neben den Regeln a + 0 = a sowie a · 1 = a ferner
Assoziativität:
(a + b) + c = a + (b + c) und (ab)c = a(bc),
Kommutativität: a + b = b + a
und ab = ba,
Distributivität: a(b + c) = ab + ac
für alle a, b, c ∈ Z.
§3 Die ganzen und die rationalen Zahlen
Die Null ’0’ tritt dabei als die Äquivalenzklasse [k, k] mit einer
beliebigen natürlichen Zahl k auf und das additiv Inverse
−[n + 1, 1] einer beliebigen, aber festen natürlichen Zahl
n = [n + 1, 1] erklärt sich als [1, n + 1].
Zur Vereinfachung ersetzen wir die Äquivalenzklassenschreibweise
im Folgenden durch unsere übliche Notation ganzer Zahlen.
Es gelten die üblichen (und wichtigen) Rechengesetze, nämlich
neben den Regeln a + 0 = a sowie a · 1 = a ferner
Assoziativität:
(a + b) + c = a + (b + c) und (ab)c = a(bc),
Kommutativität: a + b = b + a
und ab = ba,
Distributivität: a(b + c) = ab + ac
für alle a, b, c ∈ Z.
§3 Die ganzen und die rationalen Zahlen
Die Null ’0’ tritt dabei als die Äquivalenzklasse [k, k] mit einer
beliebigen natürlichen Zahl k auf und das additiv Inverse
−[n + 1, 1] einer beliebigen, aber festen natürlichen Zahl
n = [n + 1, 1] erklärt sich als [1, n + 1].
Zur Vereinfachung ersetzen wir die Äquivalenzklassenschreibweise
im Folgenden durch unsere übliche Notation ganzer Zahlen.
Es gelten die üblichen (und wichtigen) Rechengesetze, nämlich
neben den Regeln a + 0 = a sowie a · 1 = a ferner
Assoziativität:
(a + b) + c = a + (b + c) und (ab)c = a(bc),
Kommutativität: a + b = b + a
und ab = ba,
Distributivität: a(b + c) = ab + ac
für alle a, b, c ∈ Z.
§3 Die ganzen und die rationalen Zahlen
Die Null ’0’ tritt dabei als die Äquivalenzklasse [k, k] mit einer
beliebigen natürlichen Zahl k auf und das additiv Inverse
−[n + 1, 1] einer beliebigen, aber festen natürlichen Zahl
n = [n + 1, 1] erklärt sich als [1, n + 1].
Zur Vereinfachung ersetzen wir die Äquivalenzklassenschreibweise
im Folgenden durch unsere übliche Notation ganzer Zahlen.
Es gelten die üblichen (und wichtigen) Rechengesetze, nämlich
neben den Regeln a + 0 = a sowie a · 1 = a ferner
Assoziativität:
(a + b) + c = a + (b + c) und (ab)c = a(bc),
Kommutativität: a + b = b + a
und ab = ba,
Distributivität: a(b + c) = ab + ac
für alle a, b, c ∈ Z.
§3 Die ganzen und die rationalen Zahlen
Die Null ’0’ tritt dabei als die Äquivalenzklasse [k, k] mit einer
beliebigen natürlichen Zahl k auf und das additiv Inverse
−[n + 1, 1] einer beliebigen, aber festen natürlichen Zahl
n = [n + 1, 1] erklärt sich als [1, n + 1].
Zur Vereinfachung ersetzen wir die Äquivalenzklassenschreibweise
im Folgenden durch unsere übliche Notation ganzer Zahlen.
Es gelten die üblichen (und wichtigen) Rechengesetze, nämlich
neben den Regeln a + 0 = a sowie a · 1 = a ferner
Assoziativität:
(a + b) + c = a + (b + c) und (ab)c = a(bc),
Kommutativität: a + b = b + a
und ab = ba,
Distributivität: a(b + c) = ab + ac
für alle a, b, c ∈ Z.
§3 Die ganzen und die rationalen Zahlen
Wir folgen der Konvention Punktrechnung vor Strichrechnung und
lassen das Multiplikationssymbol nach Belieben aus. Ferner
schreiben wir statt a + (−b) im Folgenden a − b, womit nun
beliebige Differenzen ganzer Zahlen eingeführt sind.
Nun verifizieren wir eine weitere, uns intuitiv klare Aussage über
ganze Zahlen:
Gilt ab = 0 für a, b ∈ Z, dann ist a = 0 oder b = 0.
Nach Definition der Multiplikation gilt nämlich
[a+1, 1]·[b+1, 1] = [ab+a+b+1, a+1+b+1] = [ab+1, 1] 6= [1, 1].
Also besteht die Aussage für natürliche Zahlen a, b. In ähnlicher
Weise schließt man bei den verbleibenden Fällen, wo mindestens
einer der Faktoren eine ganze, aber nicht natürliche Zahl ist.
§3 Die ganzen und die rationalen Zahlen
Wir folgen der Konvention Punktrechnung vor Strichrechnung und
lassen das Multiplikationssymbol nach Belieben aus. Ferner
schreiben wir statt a + (−b) im Folgenden a − b, womit nun
beliebige Differenzen ganzer Zahlen eingeführt sind.
Nun verifizieren wir eine weitere, uns intuitiv klare Aussage über
ganze Zahlen:
Gilt ab = 0 für a, b ∈ Z, dann ist a = 0 oder b = 0.
Nach Definition der Multiplikation gilt nämlich
[a+1, 1]·[b+1, 1] = [ab+a+b+1, a+1+b+1] = [ab+1, 1] 6= [1, 1].
Also besteht die Aussage für natürliche Zahlen a, b. In ähnlicher
Weise schließt man bei den verbleibenden Fällen, wo mindestens
einer der Faktoren eine ganze, aber nicht natürliche Zahl ist.
§3 Die ganzen und die rationalen Zahlen
Wir folgen der Konvention Punktrechnung vor Strichrechnung und
lassen das Multiplikationssymbol nach Belieben aus. Ferner
schreiben wir statt a + (−b) im Folgenden a − b, womit nun
beliebige Differenzen ganzer Zahlen eingeführt sind.
Nun verifizieren wir eine weitere, uns intuitiv klare Aussage über
ganze Zahlen:
Gilt ab = 0 für a, b ∈ Z, dann ist a = 0 oder b = 0.
Nach Definition der Multiplikation gilt nämlich
[a+1, 1]·[b+1, 1] = [ab+a+b+1, a+1+b+1] = [ab+1, 1] 6= [1, 1].
Also besteht die Aussage für natürliche Zahlen a, b. In ähnlicher
Weise schließt man bei den verbleibenden Fällen, wo mindestens
einer der Faktoren eine ganze, aber nicht natürliche Zahl ist.
§3 Die ganzen und die rationalen Zahlen
Die rationalen Zahlen sind die Brüche ba , die aus ganzen Zahlen a
und b gebildet werden können, wobei natürlich b = 0 verboten ist
und wir zudem noch für den Nenner b ∈ N fordern.
Hier tritt das Phänomen auf, dass verschiedene Brüche denselben
6
Wert besitzen können, etwa 10
25 = 15 , stets jedoch kann man einen
eindeutigen gekürzten Bruch angeben, im letzten Beispiel 25 . Dabei
wird der größte gemeinsame Teiler des Zählers a und des Nenners b
jeweils herausdividiert:
3·2
2
6
=
= .
15
3·5
5
§3 Die ganzen und die rationalen Zahlen
Die rationalen Zahlen sind die Brüche ba , die aus ganzen Zahlen a
und b gebildet werden können, wobei natürlich b = 0 verboten ist
und wir zudem noch für den Nenner b ∈ N fordern.
Hier tritt das Phänomen auf, dass verschiedene Brüche denselben
6
Wert besitzen können, etwa 10
25 = 15 , stets jedoch kann man einen
eindeutigen gekürzten Bruch angeben, im letzten Beispiel 25 . Dabei
wird der größte gemeinsame Teiler des Zählers a und des Nenners b
jeweils herausdividiert:
3·2
2
6
=
= .
15
3·5
5
§3 Die ganzen und die rationalen Zahlen
Die rationalen Zahlen sind die Brüche ba , die aus ganzen Zahlen a
und b gebildet werden können, wobei natürlich b = 0 verboten ist
und wir zudem noch für den Nenner b ∈ N fordern.
Hier tritt das Phänomen auf, dass verschiedene Brüche denselben
6
Wert besitzen können, etwa 10
25 = 15 , stets jedoch kann man einen
eindeutigen gekürzten Bruch angeben, im letzten Beispiel 25 . Dabei
wird der größte gemeinsame Teiler des Zählers a und des Nenners b
jeweils herausdividiert:
3·2
2
6
=
= .
15
3·5
5
§3 Die ganzen und die rationalen Zahlen
Wir betrachten die durch
(a, b) ∼ (c, d )
: ⇐⇒
ad = bc
auf N erklärte Äquivalenzrelation. Identifizieren wir nun das
geordnete Paar (a, b) ∈ N2 mit dem Bruch ba , so bestehen die
Äquivalenzklasse von (a, b) genau aus den Brüchen dc gleichen
Wertes, denn es gilt
c
a
=
b
d
⇐⇒
ad = bc.
Auf diese Art und Weise erhalten wir die Menge Q+ aller positiven
rationalen Zahlen ba als die Menge der Äquivalenzklassen N/ ∼.
§3 Die ganzen und die rationalen Zahlen
Wir erklären nun die Addition vermöge
a m
an + bm
+
=
b
n
bn
bzw.
(a, b) + (m, n) := (an + bm, bn)
und die Multiplikation durch
am
a m
·
=
b n
bn
bzw.
(a, b) · (m, n) := (am, bn).
Mit der Differenzenbildung (also derart wie wir Z aus N gewonnen
haben) können wir dann die Menge Q aller rationalen Zahlen
konstruieren. Dabei finden wir die ganzen Zahlen a unter den
rationalen Zahlen (a, b) als diejenigen wieder, für die b = 1 gilt.
Die Ordnungsrelationen ’<’ und ’≤’ setzen sich in natürlicher
Weise auf Q fort.
§3 Die ganzen und die rationalen Zahlen
Wir erklären nun die Addition vermöge
a m
an + bm
+
=
b
n
bn
bzw.
(a, b) + (m, n) := (an + bm, bn)
und die Multiplikation durch
am
a m
·
=
b n
bn
bzw.
(a, b) · (m, n) := (am, bn).
Mit der Differenzenbildung (also derart wie wir Z aus N gewonnen
haben) können wir dann die Menge Q aller rationalen Zahlen
konstruieren. Dabei finden wir die ganzen Zahlen a unter den
rationalen Zahlen (a, b) als diejenigen wieder, für die b = 1 gilt.
Die Ordnungsrelationen ’<’ und ’≤’ setzen sich in natürlicher
Weise auf Q fort.
§3 Die ganzen und die rationalen Zahlen
Wir erklären nun die Addition vermöge
a m
an + bm
+
=
b
n
bn
bzw.
(a, b) + (m, n) := (an + bm, bn)
und die Multiplikation durch
am
a m
·
=
b n
bn
bzw.
(a, b) · (m, n) := (am, bn).
Mit der Differenzenbildung (also derart wie wir Z aus N gewonnen
haben) können wir dann die Menge Q aller rationalen Zahlen
konstruieren. Dabei finden wir die ganzen Zahlen a unter den
rationalen Zahlen (a, b) als diejenigen wieder, für die b = 1 gilt.
Die Ordnungsrelationen ’<’ und ’≤’ setzen sich in natürlicher
Weise auf Q fort.
§3 Die ganzen und die rationalen Zahlen
Wir erklären nun die Addition vermöge
a m
an + bm
+
=
b
n
bn
bzw.
(a, b) + (m, n) := (an + bm, bn)
und die Multiplikation durch
am
a m
·
=
b n
bn
bzw.
(a, b) · (m, n) := (am, bn).
Mit der Differenzenbildung (also derart wie wir Z aus N gewonnen
haben) können wir dann die Menge Q aller rationalen Zahlen
konstruieren. Dabei finden wir die ganzen Zahlen a unter den
rationalen Zahlen (a, b) als diejenigen wieder, für die b = 1 gilt.
Die Ordnungsrelationen ’<’ und ’≤’ setzen sich in natürlicher
Weise auf Q fort.
§3 Die ganzen und die rationalen Zahlen
Eine wichtige Eigenschaft rationaler Zahlen zum Schluss: Sämtliche
linearen Gleichungen
bX + a = 0
mit rationalen Koeffizienten a, b 6= 0 sind in Q eindeutig lösbar (mit
der expliziten Lösung x = − ba ).
Frage: Was hat das mit dem aus der Schule bekannten „Dreisatz“
zu tun?
§3 Die ganzen und die rationalen Zahlen
Eine wichtige Eigenschaft rationaler Zahlen zum Schluss: Sämtliche
linearen Gleichungen
bX + a = 0
mit rationalen Koeffizienten a, b 6= 0 sind in Q eindeutig lösbar (mit
der expliziten Lösung x = − ba ).
Frage: Was hat das mit dem aus der Schule bekannten „Dreisatz“
zu tun?
§3 Die ganzen und die rationalen Zahlen
Nun ein wenig Kombinatorik, was die Kunst des Zählens ist.
Für ganze Zahlen 0 ≤ k ≤ n ist der Binomialkoeffizient definiert
durch
n
n!
=
;
k
k!(n − k)!
gesprochen „n über k“.
Satz 3.2 Die Anzahl aller k-elementigen
Teilmengen einer
n
n-elementigen Menge ist k .
Insbesondere sind Binomialkoeffizienten ganzzahlig.
Aufgabe: Berechne die Wahrscheinlichkeit eines Volltreffers beim
Lotto 6 aus 49.
§3 Die ganzen und die rationalen Zahlen
Nun ein wenig Kombinatorik, was die Kunst des Zählens ist.
Für ganze Zahlen 0 ≤ k ≤ n ist der Binomialkoeffizient definiert
durch
n
n!
=
;
k
k!(n − k)!
gesprochen „n über k“.
Satz 3.2 Die Anzahl aller k-elementigen
Teilmengen einer
n
n-elementigen Menge ist k .
Insbesondere sind Binomialkoeffizienten ganzzahlig.
Aufgabe: Berechne die Wahrscheinlichkeit eines Volltreffers beim
Lotto 6 aus 49.
§3 Die ganzen und die rationalen Zahlen
Nun ein wenig Kombinatorik, was die Kunst des Zählens ist.
Für ganze Zahlen 0 ≤ k ≤ n ist der Binomialkoeffizient definiert
durch
n
n!
=
;
k
k!(n − k)!
gesprochen „n über k“.
Satz 3.2 Die Anzahl aller k-elementigen
Teilmengen einer
n
n-elementigen Menge ist k .
Insbesondere sind Binomialkoeffizienten ganzzahlig.
Aufgabe: Berechne die Wahrscheinlichkeit eines Volltreffers beim
Lotto 6 aus 49.
§3 Die ganzen und die rationalen Zahlen
Die Binomialkoeffizienten genügen der Gleichung
n n − 1 n − 1
=
+
k −1
k
k
Hieraus ergibt sich das Pascalsche Dreieck
benannt nach Blaise Pascal (1623-1662) (der auch Induktionsbeweise
popularisierte).
§3 Die ganzen und die rationalen Zahlen
Die Binomialkoeffizienten genügen der Gleichung
n n − 1 n − 1
=
+
k −1
k
k
Hieraus ergibt sich das Pascalsche Dreieck
benannt nach Blaise Pascal (1623-1662) (der auch Induktionsbeweise
popularisierte).
§3 Die ganzen und die rationalen Zahlen
Eine wesentliche Verallgemeinerung der „binomischen Formeln“
liefert der
Satz 3.3 (Binomischer Lehrsatz) Für beliebige Zahlen x und y
gilt
n X
n n−k k
x
y .
(x + y )n =
k
k=0
Insbesondere ist
n X
n
k=0
k
= 2n .
§3 Die ganzen und die rationalen Zahlen
Eine wesentliche Verallgemeinerung der „binomischen Formeln“
liefert der
Satz 3.3 (Binomischer Lehrsatz) Für beliebige Zahlen x und y
gilt
n X
n n−k k
x
y .
(x + y )n =
k
k=0
Insbesondere ist
n X
n
k=0
k
= 2n .
Resümee
Mit einer Äquivalenzrelation vergleicht man zwei Elemente einer
gegebenen Menge; diese Relation ist per Definition reflexiv,
symmetrisch und transitiv.
Die Mengen der ganzen Zahlen Z und der rationalen Zahlen Q
wurden mit Hilfe von Äquivalenzrelationen aus der Menge der
natürlichen Zahlen konstruiert.
Addition und Multiplikation ganzer und rationaler Zahlen wurden
definiert und diese stimmen mit den uns aus der Schule vertrauten
Rechenoperationen überein.
Binomialkoeffizienten sind per Definition Quotienten ganzer Zahlen;
tatsächlich sind sie sogar ganzzahlig und zählen gewisse Teilmengen
in einer gegebenen Menge.
Resümee
Mit einer Äquivalenzrelation vergleicht man zwei Elemente einer
gegebenen Menge; diese Relation ist per Definition reflexiv,
symmetrisch und transitiv.
Die Mengen der ganzen Zahlen Z und der rationalen Zahlen Q
wurden mit Hilfe von Äquivalenzrelationen aus der Menge der
natürlichen Zahlen konstruiert.
Addition und Multiplikation ganzer und rationaler Zahlen wurden
definiert und diese stimmen mit den uns aus der Schule vertrauten
Rechenoperationen überein.
Binomialkoeffizienten sind per Definition Quotienten ganzer Zahlen;
tatsächlich sind sie sogar ganzzahlig und zählen gewisse Teilmengen
in einer gegebenen Menge.
Resümee
Mit einer Äquivalenzrelation vergleicht man zwei Elemente einer
gegebenen Menge; diese Relation ist per Definition reflexiv,
symmetrisch und transitiv.
Die Mengen der ganzen Zahlen Z und der rationalen Zahlen Q
wurden mit Hilfe von Äquivalenzrelationen aus der Menge der
natürlichen Zahlen konstruiert.
Addition und Multiplikation ganzer und rationaler Zahlen wurden
definiert und diese stimmen mit den uns aus der Schule vertrauten
Rechenoperationen überein.
Binomialkoeffizienten sind per Definition Quotienten ganzer Zahlen;
tatsächlich sind sie sogar ganzzahlig und zählen gewisse Teilmengen
in einer gegebenen Menge.
II. Teilbarkeitslehre