1. Rationale und irrationale Zahlen 1.1. Quadratwurzeln

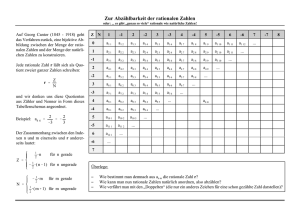
1 Rationale und irrationale Zahlen
Klasse 9c
1. Rationale und irrationale Zahlen
1.1. Quadratwurzeln
Definition:
Die Quadratwurzel aus einer rationalen Zahl r ≥ 0 , notiert
r , ist diejenige nichtnegative Zahl,
deren Quadrat r ergibt.
r heißt Radikand der Wurzel und darf nicht negativ sein.
Wurzeln lassen sich näherungsweise bestimmen, indem die gesuchte Wurzel mit Hilfe einer
Intervallschachtelung beliebig genau eingegrenzt wird.
Die Quadratwurzel aus einer rationalen Zahl r ≥ 0 ist die nichtnegative Lösung der Gleichung
x2 = r .
Wenn die Gleichung x 2 = r mit r ≥ 0 in _ lösbar ist, dann hat sie die beiden Lösungen
r und
− r.
Es gibt Zahlen, die keine rationalen Zahlen sind. Insbesondere kann man die Länge der Diagonalen
d in einem Quadrat mit der Seitenlänge 1 LE nicht mit einer rationalen Zahl angeben.
Warum
2 keine rationale Zahl sein kann: Der Widerspruchsbeweis des Euklid (um 300 v. Chr.)
(1) Wir nehmen an, dass
2=
p
mit teilerfremden Zahlen p und q ist.
q
(2) Dann gilt nach dem Quadrieren: 2 =
p2
.
q2
(3) Daraus folgt leicht: 2q 2 = p 2 .
(4) Damit muss also p 2 durch 2 teilbar sein und infolge dessen auch p.
(5) Wir setzen nun p = 2r .
(6) So folgt: q 2 = 2r 2 .
(7) Also ist wieder q 2 durch 2 teilbar und genauso auch q.
Das allerdings ist ein Widerspruch zu unserer Annahme:
2 kann keine rationale Zahl sein.