Institut für Informatik Lehrstuhl f ¨ur Informatik 15 Computer

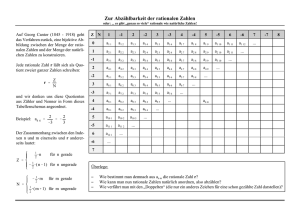
Institut für Informatik
Lehrstuhl für Informatik 15
Computer Graphik & Visualisierung
Diskrete Strukturen I
Wintersemester 2006/2007
Übungsblatt 1
Seite 1 von 2
Prof. R. Westermann, J. Schneider, J. Georgii, S. Pott
TU München, 20.10.2006
Lösungen zu Diskrete Strukturen I (Blatt 1)
Aufgabe 1
[3 Punkte] Rationale Zahlen
Seien ba und dc zwei beliebige rationale Zahlen. Dann sind also a und b bzw. c und d teilerfremd. Zu
zeigen ist nun, dass es mindestens eine weitere rationale Zahl zwischen ba und dc gibt. Betrachte also
die folgende Zahl:
ad + bc
c
1 a
=
+
2 b d
2bd
Diese Zahl liegt nun genau zwischen den beiden ursprünglichen rationalen Zahlen. Sorgt man nun
weiterhin dafür dass ad + bc und 2bd teilerfremd sind (Euklidischer grösster gemeinsamer Teiler),
dann erhält man eine neue Repräsentation ef , welche noch immer zwischen den beiden ursprünglichen Zahlen liegt. Dieses Verfahren kann man nun wiederholen, um weitere Zahlen zwischen ba , dc
und ef zu finden, usw. - somit liegen also unendlich viele Zahlen zwischen zwei beliebigen rationalen
Zahlen, die Menge Q der rationalen Zahlen ist also dicht.
Aufgabe 2
[6 Punkte] Abzählbarkeit der rationalen Zahlen
Jede rationale Zahl lässt sich als Quotient ba darstellen. Die Idee, um die Abzählbarkeit zu zeigen, besteht darin, die Ebene, die durch die ganzen Zahlen a und b aufgespannt wird sequentiell zu durchlaufen. Der Beweis geht auf Cantor zurück und heißt seitdem Cantors erstes Diagonalargument:
a/b
1
2
3
4
5
···
1
1/1 1/2 1/3 1/4 1/5 · · ·
2
2/1 2/2 2/3 2/4 2/5 · · ·
3
3/1 3/2 3/3 3/4 3/5 · · ·
4/1 4/2 4/3 4/4 4/5 · · ·
4
5
5/1 5/2 5/3 5/4 5/5 · · ·
..
..
..
..
..
..
..
.
.
.
.
.
.
.
Dieses Schema kann man entlang der Diagonalen von links unten nach rechts oben durchlaufen (unendlich lange), und jede rationale Zahl wird irgendwann ”besucht”. Also 1/1, 2/1, 1/2, 3/1, 2/2,
1/3, 4/1, · · · . Beachten muss man hierbei noch, dass man einige Zahlen mehrfach besucht (z.B.
1 = 1/1 = 2/2 = · · · ). Daher werden die Zahlen beim Ablaufen einfach übersprungen, die man
schon vorher besucht hatte (Man überspringt Zahlen, die man kürzen kann.).
Wie muss man das Schema erweitern, um auch nicht-positive rationale Zahlen zu berücksichtigen?
Seite 2 von 2
Aufgabe 3 [5 Punkte] Wahrheitstabellen
A B C A → B A → C B ∨ C ( A → B) ∨ ( A → C )
1 1 1
1
1
1
1
0 1 1
1
1
1
1
0
1
1
1
1 0 1
0 0 1
1
1
1
1
1 1 0
1
0
1
1
0 1 0
1
1
1
1
0
0
0
0
1 0 0
0 0 0
1
1
0
1
[7×1 Punkte]
Aufgabe 4
(( A → B) ∨ ( A → C )) ∧ ( B ∨ C )
1
1
1
1
1
1
0
0
Äquivalenzregeln der Logik
a) p ↔ q und ( p → q) ∧ (q → p) sind äquivalent. Beweis über Wertetabelle:
p
1
0
1
0
q
1
1
0
0
p↔q
1
0
0
1
p→q
1
1
0
1
q→p
1
0
1
1
( p → q ) ∧ (q → p)
1
0
0
1
b) ( p ∧ q) ∨ (¬ p ∧ ¬q) = ( p ∨ ¬ p) ∧ ( p ∨ ¬q) ∧ (q ∨ ¬ p) ∧ (q ∨ ¬q)
true ∧ ( p ∨ ¬q) ∧ (q ∨ ¬ p) ∧ true = (q → p) ∧ ( p → q) =
( p ↔ q)
=
c) (¬ p ∧ ( p → q)) → ¬q = ¬(¬ p ∧ (¬ p ∨ q)) ∨ ¬q =
¬((¬ p ∧ ¬ p) ∨ (¬ p ∧ q)) ∨ ¬q = ¬(¬ p ∨ (¬ p ∧ q)) ∨ ¬q =
( p ∧ ( p ∨ ¬q)) ∨ ¬q = ( p ∨ ¬q) ∧ ( p ∨ ¬q ∨ ¬q) =
( p ∨ ¬q) ∧ ( p ∨ ¬q) = ( p ∨ ¬q)
Dieser Ausdruck ist nicht für alle Belegungen wahr, also keine Tautologie.
d) (¬q ∧ ( p → q)) → ¬ p = ¬(¬q ∧ (¬ p ∨ q)) ∨ ¬ p
(q ∨ ( p ∧ ¬q)) ∨ ¬ p = ((q ∨ p) ∧ (q ∨ ¬q)) ∨ ¬ p
((q ∨ p) ∧ true) ∨ ¬ p = q ∨ p ∨ ¬ p =
q ∨ true = true
Der Ausdruck ist also eine Tautologie.
e) p → q
=
=
¬p ∨ q
¬(¬q) ∨ (¬ p)
=
=
=
¬q → ¬ p
f) ( p → q) ∧ (q → r) → ( p → r) = ((¬ p ∨ q) ∧ (¬q ∨ r)) → (¬ p ∨ r) =
¬((¬ p ∨ q) ∧ (¬q ∨ r)) ∨ (¬ p ∨ r) = ( p ∧ ¬q) ∨ (q ∧ ¬r) ∨ ¬ p ∨ r =
¬ p ∨ ( p ∧ ¬q) ∨ r ∨ (q ∧ ¬r) = ((¬ p ∨ p) ∧ (¬ p ∨ ¬q)) ∨ ((r ∨ q) ∧ (r ∨ ¬r))
(¬ p ∨ ¬q) ∨ (r ∨ q) = q ∨ ¬q ∨ r ∨ ¬ p = true
Der Ausdruck ist also eine Tautologie.
g) ( p → q) ∧ ( p → r)
Aufgabe 5
[4×1 Punkte]
=
(¬ p ∨ q) ∧ (¬ p ∨ r)
=
¬ p ∨ (q ∧ r)
=
=
p → (q ∧ r)
Aussagen
a) ”Wenn alle natürlichen Zahlen gerade sind, dann liegt München in Frankreich.” ist wahr.
b) ”Wenn Frau Merkel Kanzlerin ist, dann ist Köln die Hauptstadt Deutschlands.” ist falsch.
c) ”Wenn Nürnberg die Hauptstadt Bayerns ist, dann ist Herr Stoiber Ministerpräsident.” ist wahr.
d) ”Wenn die TU Exzellenz-Universität ist, dann wird mit Bier gefeiert.” ist wahr.