Wahrscheinlichkeitsrechnung

Klasse
Art
Schwierigkeit
Thema
Nr.
10
Üben
XX
Wahrscheinlichkeitsrechnung
1
Daumenlutschen
Neun von zehn Ungeborenen bevorzugen im Mutterleib den rechten Daumen zum Lutschen. Forscher
fanden heraus, dass alle Kinder, die rechts genuckelt hatten, im Alter von 10 bis 12 Jahren Rechtshänder
waren. Zwei Drittel der Kinder, die im Mutterleib am linken Daumen lutschten, waren Linkshänder.
(a) Wie viel Prozent der Kinder sind Linkshänder geworden, wie viel Prozent Rechtshänder?
(b) Mit welcher Wahrscheinlichkeit hat ein Rechtshänder vor der Geburt am linken Daumen
genuckelt?
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Lösung
XX
Wahrscheinlichkeitsrechnung
1
Angaben aus dem Text:
R: „Rechtshänder“
RL: „lutscht am rechten Daumen“
PRL ( R ) = 23
P ( RL ) = 90%
PRL ( R ) = 100%
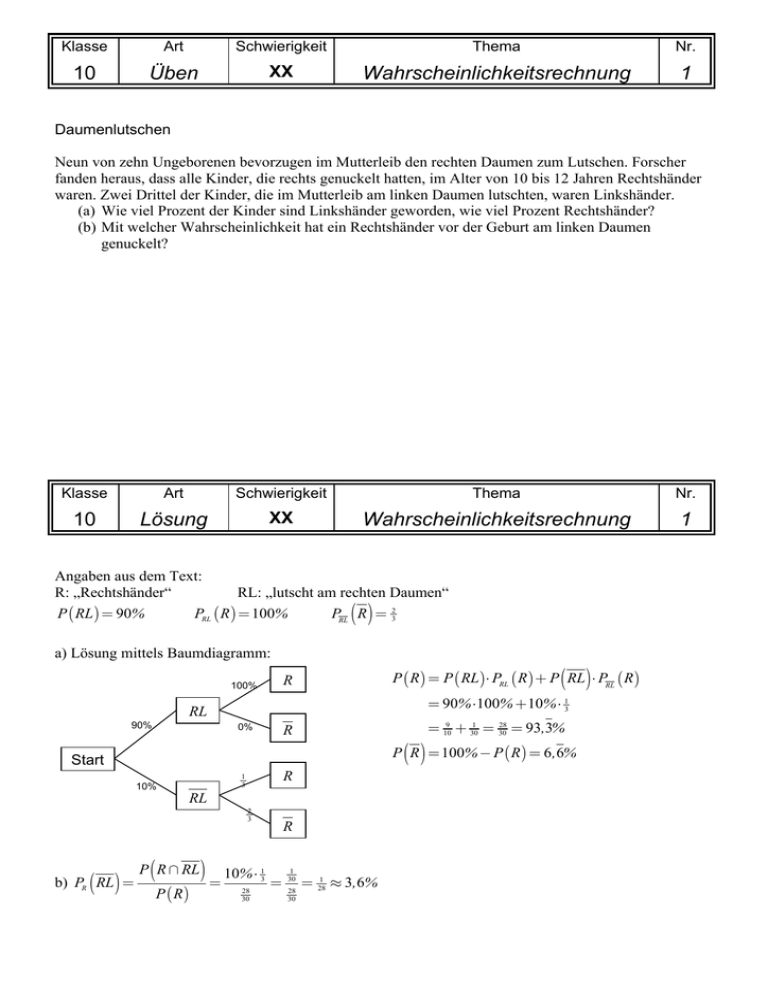
a) Lösung mittels Baumdiagramm:
P ( R ) = P ( RL)⋅ PRL ( R ) + P ( RL)⋅ PRL ( R )
R
100%
= 90% ⋅100% + 10% ⋅ 13
RL
90%
0%
= 109 + 301 = 3028 = 93,3%
R
P ( R ) = 100% − P ( R ) = 6 ,6%
Start
R
1
3
10%
RL
2
3
b) PR ( RL) =
P ( R ∩ RL)
P ( R)
=
10% ⋅ 13
28
30
R
=
1
30
28
30
= 281 ≈ 3, 6%
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Üben
XX
Wahrscheinlichkeitsrechnung
2
Rauchen
Die Schüler des Karlsgymnasiums sind zu 60% Jungen. Von allen Schülern rauchen 10%. Unter den
Schülerinnen rauchen 15%.
(a) Berechnen Sie den Anteil der weiblichen Raucher unter allen Schülern.
(b) Mit welcher Wahrscheinlichkeit ist ein beliebig herausgegriffener Schüler
i.
weiblich, falls „er“ raucht?
ii.
männlich, falls er raucht?
iii.
Raucher, falls er männlich ist?
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Lösung
XX
Wahrscheinlichkeitsrechnung
2
Daten aus der Angabe
M=„männlich“, W=„weiblich“, R=„der Schüler / die Schülerin raucht“
P ( M ) = 60%
P ( R ) = 10%
PW ( R ) = 15%
a) P (W ∩ R ) = PW ( R )⋅ P (W ) = 15% ⋅ 40% = 0 ,15 ⋅ 0 , 4 = 0 , 06 = 6%
b) i) PR (W ) =
P (W ∩ R )
P ( R)
=
0,06
= 60%
10%
ii) PR ( M ) = 1− PR (W ) = 1− 60% = 1− 0 ,6 = 0 , 4 = 40%
iii) PM ( R ) =
P(R ∩ M )
P (M )
=
PR ( M )⋅ P ( R )
P (M )
=
0, 4 ⋅ 0 ,1 0, 04
=
= 6 ,6%
0,6
0,6
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Üben
X
Wahrscheinlichkeitsrechnung
3
Baumdiagramme und Vierfeldertafel
Betrachten Sie folgenden Zeitungsartikel
a) Stellen Sie die Informationen des Zeitungsartikels in einem zweistufigen Baum dar (1. Stufe:
Kinder, 2. Stufe: Eltern).
b) Stellen Sie eine Vierfeldertafel dazu auf.
c) Entwickeln Sie aus b) das umgekehrte Baumdiagramm (1. Stufe: Eltern, 2. Stufe: Kinder).
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Lösung
X
Wahrscheinlichkeitsrechnung
3
a)
35%
Gy
Gy
65%
37%
H/Rs
Start
63%
8%
H/Rs
Gy
92%
H/Rs
1. Stufe: Kinder
2. Stufe: Eltern
b)
Eltern Gy
0,37 ⋅ 0,35 = 12 ,95%
0, 63 ⋅ 0, 08 = 5,04%
17,99%
Kind Gy
Kind H/Rs
Eltern H/Rs
0,37 ⋅ 0,65 = 24,05%
0, 63⋅ 0,92 = 57 ,96%
82,01%
c)
12,95%:17,99%≈71,98%
Gy
Gy
28,02%
17,99%
H/Rs
Start
82,01%
24,05%:82,01%≈29,33%
H/Rs
70,67%
1. Stufe: Eltern
Gy
H/Rs
2. Stufe: Kinder
37%
63%
100%
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Üben
XX
Wahrscheinlichkeitsrechnung
4
Aufgaben zur Anwendung
Der Lehrer bringt zwei faire Würfel mit. Auf dem ersten Würfel sind fünf Flächen mit „Ja“
überschrieben, auf dem anderen Würfel nur zwei Flächen. Auf den restlichen Flächen steht „Nein“.
Nachdem der Lehrer diese Würfel gezeigt hat, nimmt er sie verdeckt jeweils in die eine oder die andere
Hand. Peter muss nun blind nach Zufall einen Würfel auswählen, den er dann - für die Klasse verdeckt vom Lehrer erhält.
Peter würfelt mit diesem Würfel dreimal - weiterhin für die Klasse verdeckt – und nennt als Ergebnisse:
„Ja, Ja, Nein.“
Die übrige Klasse soll nun wetten, ob Peter den ersten Würfel oder den zweiten Würfel erhielt.
Baut euch selber Würfel und überprüft eure erstellten Berechnungen!
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Lösung
XX
Wahrscheinlichkeitsrechnung
4
Zu bestimmen sind die Wahrscheinlichkeiten P" Ja ,Ja ,Nein" (" 1" ) bzw. P" Ja ,Ja ,Nein" (" 2" )
P (" 1" ) = 50%,P (" 2" ) = 50%
Die Ergebnisse werden unter Berücksichtigung der Reihenfolge genannt.
25
P" 1" (" Ja,Ja,Nein" ) = 56 ⋅ 65 ⋅ 16 = 216
P" 2" (" Ja,Ja,Nein" ) = 26 ⋅ 26 ⋅ 64 =
16
216
P (" Ja,Ja,Nein" ) = P (" 1" ∩" Ja,Ja,Nein" ) + P (" 2" ∩" Ja,Ja,Nein" )
= P (" 1" )⋅ P" 1" (" Ja,Ja,Nein" ) + P (" 2" )⋅ P" 2" (" Ja,Ja,Nein" )
25
16
41
= 0,5 ⋅ 216
+ 0 ,5 ⋅ 216
= 432
25
P (" 1" ∩" Ja,Ja,Nein" ) 0,5 ⋅ 216
25
P" Ja ,Ja ,Nein" (" 1" ) =
= 41 =
≈ 60 ,98%
P (" Ja,Ja,Nein" )
41
432
P" Ja ,Ja ,Nein" (" 2" ) = 1− P" Ja ,Ja ,Nein" (" 1" ) ≈ 39 ,02%
Mit einer Wahrscheinlichkeit von 61% hat Peter den Würfel 1 gezogen, mit 39% den Würfel 2.
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Üben
XX
Wahrscheinlichkeitsrechnung
5
BSE
(a) Recherchieren Sie, was man unter BSE und nCJK versteht. Tragen Sie Informationen zusammen, was zum Ausbruch
und zur Verbreitung von BSE geführt hat.
(b) Wie würden Sie die Sicherheit des erwähnten Tests beschreiben? Wie wirkt sich der Fehler des Tests auf die
betroffenen Bauern und Verbraucher aus?
(c) In der Bundesrepublik wurden in den Jahren um 2000 jährlich etwa 480000 Rinder geschlachtet. Die
Verbraucherschutzministerin Renate Künast hat im Jahr 2001 angegeben, „dass in diesem Jahr 500 BSE-Fälle
erwartet werden“. Alle geschlachteten Rinder werden mit einem Schnelltest untersucht. Dieser Schnelltest
identifiziert mit einer Wahrscheinlichkeit von 95% die erkrankten Rinder korrekt, er gibt aber auch in 3% der Fälle
gesunde Rinder als BSE erkrankt aus. Bestimmen Sie die Wahrscheinlichkeit, dass ein Rind, das positiv getestet
wurde, auch wirklich krank ist.
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Lösung
XX
Wahrscheinlichkeitsrechnung
5
Zahlen aus der Angabe:
500
1
P" krank" (" Test positiv" ) = 95% , P" gesund " (" Test positiv") = 3% , P (" krank" ) = 480000
= 960
gesucht ist: P" Test positiv" (" krank" )
P" Test positiv" (" krank" ) =
=
=
P (" Test positiv" ∩" krank" )
P (" Test positiv" )
P (" krank" )⋅ P" krank" (" Test positiv" )
P (" krank" )⋅ P" krank" (" Test positiv" ) + P (" gesund " )⋅ P" gesund " ("Test positiv")
⋅ 95%
≈ 3, 2%
959
1
960 ⋅ 95% + 960 ⋅ 3%
1
960
Nur 3,2% der positiv getesteten Rinder sind wirklich krank. Die Fehlerquote ist sehr hoch.
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Üben
X
Wahrscheinlichkeitsrechnung
6
Aus den natürlichen Zahlen von 1 bis 100 wird eine Zahl zufällig ausgewählt. Mit welcher
Wahrscheinlichkeit ist diese Zahl
(a) ein Vielfaches von 2, wenn man weiß, dass sie ein Vielfaches von 4 ist?
(b) ein Vielfaches von 4, wenn man weiß, dass sie ein Vielfaches von 2 ist?
(c) ein Vielfaches von 4, wenn man weiß, dass sie ein Vielfaches von 7 ist?
(d) ein Vielfaches von 4, wenn man weiß, dass sie ein gemeinsames Vielfaches von 5 und 6
ist?
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Lösung
X
Wahrscheinlichkeitsrechnung
6
(a) 100%
25
= 50%
(b)
50
(c) P7|X (4 | X ) =
=
P (4 | X und 7 | X )
P (7 | X )
=
P (28 | X )
P (7 | X )
{28,56,74}
{7 ,14, 21, 28,35, 42, 49,56, 63,70,77 ,84,91,98}
P (4 | X und 5 | X und 6 | X ) P (60 | X )
(d) P5|X und 6|X (4 | X ) =
=
P (5 | X und 6 | X )
P (30 | X )
{60}
1
=
= ≈ 33,3%
{30,60,90} 3
=
3
≈ 21, 4%
14
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Üben
XX
Wahrscheinlichkeitsrechnung
7
In der Bundesrepublik wurden in den Jahren um
2000 jährlich etwa 480000 Rinder geschlachtet. Die
Verbraucherschutzministerin Renate Künast hat im
Jahr 2001 angegeben, „dass in diesem Jahr 500 BSEFälle erwartet werden“. Alle geschlachteten Rinder
werden mit einem Schnelltest untersucht. Dieser
Schnelltest identifiziert mit einer Wahrscheinlichkeit
von 95% die erkrankten Rinder korrekt, er gibt aber
auch in 3% der Fälle gesunde Rinder als BSEerkrankt aus.
a) Bestimme die Wahrscheinlichkeit, dass ein
Rind, das positiv getestet wurde, auch
wirklich krank ist.
b) Da Schnelltests nicht absolut sicher sind,
treten immer Fehler auf. Wie wirken sich die
Fehler aus, wenn der Anteil der BSEErkrankungen ansteigt?
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Lösung
XX
Wahrscheinlichkeitsrechnung
7
Modellierung:
P = „Der Test ist positiv“
B = „Das Rind trägt den BSE-Erreger“
Daten aus der Angabe:
500
1
P ( B) =
=
480000 960
PB ( P ) = 95%
PB ( P ) = 3%
Visualisierung: Ich würde Ihnen einen Baum empfehlen, der B an der ersten Stufe hat.
a) Berechnung:
1
P ( P ∩ B)
P ( B )⋅ PB ( P )
960 ⋅ 0 , 95
=
= 1
≈ 0 , 03197 = 3,197%
PP ( B ) =
P ( P)
P ( B )⋅ PB ( P ) + P ( B )⋅ PB ( P ) 960 ⋅ 0 ,95 + 959
960 ⋅ 0 , 03
Das ist überraschend wenig. Das liegt an der Tatsache, dass immerhin 3% aller nicht-infizierten
Rinder falsch-positiv getestet werden und immerhin 14385. Bei nur 500 infizierten ist also die
Fehlerquote sehr hoch.
b) Wenn der Anteil der BSE-Erkrankungen ansteigt, dann steigt auch die in a) berechnete
2
960 ⋅ 0 ,95
Wahrscheinlichkeit z.B. PP ( B ) = 2
≈ 6, 2% . Die Fehlerquote sinkt also, denn es
958
960 ⋅ 0 , 95 + 960 ⋅ 0 , 03
sinkt ja auch die Zahl der falsch-positiv getesteten Rinder.
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Üben
XX
Wahrscheinlichkeitsrechnung
8
Beim Lehrer Kreissel kommt es in der Klasse 10A in einer Unterrichtsstunde mit einer
Wahrscheinlichkeit von 25% zu einer Unterrichtsstörung. Im Falle einer Unterrichtsstörung
erhöht sich der Blutdruck von Herrn Kreissel mit 80% Wahrscheinlichkeit. Jedoch kommt es bei
Herrn Kreissel auch ohne Unterrichtsstörung mit einer Wahrscheinlichkeit von 10% zu erhöhtem
Blutdruck.
a) Mit welcher Wahrscheinlichkeit ist es in einer 10A-Stunde laut und die Lehrkraft
hat erhöhten Blutdruck?
b) Mit welcher Wahrscheinlichkeit hat der Lehrer in einer 10A-Stunde keinen
erhöhten Blutdruck?
c) Mit welcher Wahrscheinlichkeit ist es in der 10A laut, wenn der Lehrer erhöhten
Blutdruck hat?
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Lösung
XX
Wahrscheinlichkeitsrechnung
8
Modellierung:
B = „Der Lehrer Kreissel hat erhöhten Blutdruck“
L = „Die Klasse 10A ist laut“
P ( L) = 25%
PL ( B ) = 80%
PL ( B ) = 10%
Visualisierung: Ich empfehle ein Baumdiagramm mit L an der ersten Stufe.
Berechnung:
a) P ( L ∩ B ) = P ( L)⋅ PL ( B ) = 0 , 25 ⋅ 0 ,80 = 0 , 2 = 20%
b) P ( B ) = P ( L )⋅ PL ( B ) + P ( L)⋅ PL ( B ) = 0, 25 ⋅ 0, 20 + 0, 75 ⋅ 0,90 = 72,5%
c) PB ( L) =
P ( L ∩ B)
P ( B)
=
P ( L )⋅ PL ( B )
P ( L)⋅ PL ( B ) + P ( L)⋅ PL ( B )
=
0 , 25 ⋅ 0 ,80
≈ 72 , 7%
0 , 25 ⋅ 0 ,8 + 0 , 75 ⋅ 0 ,1
nicht ernst gemeinte Diskussion: Wenn der arme Herr Kreissel irgendwann an überhöhtem
Blutdruck stirbt, dann war die 10A mit großer Wahrscheinlichkeit daran Schuld.
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Üben
XX
Wahrscheinlichkeitsrechnung
1
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Lösung
XX
Wahrscheinlichkeitsrechnung
1
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Üben
XX
Wahrscheinlichkeitsrechnung
1
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Lösung
XX
Wahrscheinlichkeitsrechnung
1
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Üben
XX
Wahrscheinlichkeitsrechnung
1
Klasse
Art
Schwierigkeit
Thema
Nr.
10
Lösung
XX
Wahrscheinlichkeitsrechnung
1