U - Elementarteilchenphysik Uni Rostock

8. Leitwertmessung / Ionentransport
Ziele:
Bei der Analyse chemischer Prozesse müssen Daten ermittelt werden. Dabei wandeln geeignete
Sensoren die gesuchte Größe in einen Strom oder eine Spannung um. In diesem Experiment sollen
Sie die Leitfähigkeit von Elektrolyten untersuchen. Die Messschaltungen sind entsprechend der
vorgefundenen Situation zu optimieren.
Aufgaben:
1. Ermitteln Sie den Leitwert von
a) destilliertem Wasser b) Leitungswasser c) einer physiologischen Kochsalzlösung.
2. Benutzen Sie dazu die Digitalmultimeter. Beurteilen Sie die möglichen Schaltungsvarianten.
Grundlagen:
Zur Messung werden zwei Elektroden in den Elektrolyten getaucht. An diese wird die Spannung
angeschlossen. Entsprechend der stark unterschiedlichen Konzentration an H+ und (OH)–-Ionen,
die wesentlich zur elektrischen Leitung beitragen, werden stark unterschiedliche Leitwerte für das
destillierte Wasser bzw. die Kochsalzlösung zu erwarten sein. Um eine zu starke Gasentwicklung
und eine Polarisation im Elektrolyten zu vermeiden, wird eine Wechselspannung benutzt. Die
Messung ist von der Frequenz weitgehend unabhängig. Als Spannungsquelle benutzen Sie ein
Stromversorgungsgerät. Die Bedienung sämtlicher zu benutzenden Geräte wird Ihnen zu Beginn
des Experiments vom Betreuer erklärt.
Den Leitwert G ermitteln Sie, indem Sie den Strom I durch den Elektrolyten und die Spannung
U an den Elektroden gleichzeitig messen. G entspricht dem Kehrwert des Ohmschen Widerstandes
und die Einheit heißt Siemens (S = 1/Ω). G errechnet sich nach der Formel
G=
I
U
.
(8.1)
Grundsätzlich wird zur Messung das Voltmeter parallel und das Amperemeter in Reihe zum
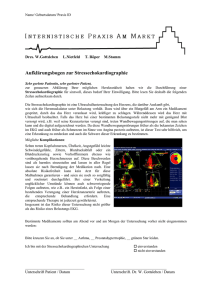
Widerstand (Elektrolyt) geschaltet! Für die aufzubauende Schaltung gibt es die beiden hier abgebildeten Möglichkeiten. Für eine genaue Messung hat dabei der Innenwiderstand des Voltmeters
unendlich groß zu sein und der Innenwiderstand des Amperemeters sollte nahezu 0 Ω betragen.
Tatsächlich weichen die Innenwiderstände der Messgeräte von diesen Idealvorstellungen etwas ab
und man misst jeweils entweder die Stromstärke oder die Spannung korrekt. Diese Schaltungen
nennt man auch stromrichtige Schaltung – man misst exakt den Strom, der durch den Elektrolyten
fließt, aber die gemessene Spannung U setzt sich aus der Spannung UE am Elektrolyten und dem
Spannungsabfall UA am Amperemeter zusammen – oder spannungsrichtige Schaltung – man misst
die Spannung direkt und korrekt am Elektrolyten, aber hier zeigt das Amperemeter die Summe I
RV
G
RV
V
U
IE =I
UE
V
UE
G
RA
A
I
V
RA
A
IE I
UA
UA
U
U
stromrichtige Schaltung
spannungsrichtige Schaltung
36
der Ströme durch den Elektrolyten IE und durch das Voltmeter IV an. Es ist nicht möglich, beide
Größen (IE, UE) unverfälscht zu messen. Einzelmessungen, die nacheinander durchgeführt werden,
liefern Werte, die auch durch die Messgeräte beeinflusst sind. Man erhält kein korrektes Messwertpaar. Deshalb ist es gegebenenfalls notwendig, die Größe der Verfälschung zu ermitteln und
die Messwerte zu berichtigen. Jedoch zeigen die Gleichungen
IE
IE
IE
=
=
U E U − U A U − I E ⋅ RA
stromrichtige Schaltung
G=
(8.2) und
G=
IE I − IV
=
=
UE
UE
UE
RV
UE
I−
,
(8.3)
spannungsrichtige Schaltung
dass mit günstigen Innenwiderständen der Messgeräte mit der Relation U/IE » RA bei stromrichtiger
Schaltung und mit UE/I « RV bei spannungsrichtiger Schaltung diese Korrektur nicht erforderlich
ist.
Die Widerstände RA und RV sind vom eingestellten Messbereich abhängige Geräteparameter.
Eine Korrektur der Strom- und Spannungswerte ist überflüssig, wenn die Verfälschung (erfassbarer
systematischer Fehler) kleiner als die halbe Messunsicherheit ∆U bzw. ∆I ist, die durch die Güteklasse des Messgerätes angegeben wird.
Durchführung:
Für alle drei zu untersuchenden Flüssigkeiten sind die Leitwerte mit der strom- und der spannungsrichtigen Schaltung für die gegebene Elektrodenanordnung zu ermitteln. Entsprechend der zu erwartenden unterschiedlichen Leitfähigkeiten verwenden Sie Wechselspannungen von ungefähr
50 V für dest. Wasser, 20 V für Leitungswasser und 2 V für die Kochsalzlösung. Stellen Sie zu
Messbeginn jeweils große bzw. ausreichende Messbereiche (Wechselstrom) ein.
Auswertung:
Berechnen Sie die Leitwerte für die drei Elektrolyte jeweils für die strom- und spannungsrichtige
Schaltung. Vergleichen Sie die Ergebnisse. Liegen Unterschiede außerhalb der Unsicherheiten von
G mit
∆G
∆U
∆I
=
+
(8.4)
G
U
I
vor? Bei welchen der Elektrolyte (dest. Wasser oder Kochsalzlösung) ist die strom- bzw. die spannungsrichtige Schaltung zu bevorzugen?
Fragen:
1. Wie lauten das 1. und 2. Kirchhoffsche Gesetz (Regel) (Knotenpunkt- und Maschensatz).
2. Wie unterscheiden sich die Innenwiderstände von Voltmetern und Amperemetern?
3. Wie sind diese Geräte in elektrische Schaltungen einzufügen?
4. Welche Ungenauigkeiten entstehen bei der Leitwert- oder Widerstandsbestimmung durch
Strom- und Spannungsmessung infolge der Innenwiderstände von Volt- und Amperemetern?
Erläutern Sie die Formeln (8.2) und (8.3).
Literatur:
/1/ Geschke (Ilberg): Physikalisches Praktikum
/2/ Walcher: Praktikum der Physik
37
9. Messen mit dem Digitaloszilloskop / EKG
Ziele:
Zahlreiche Körperfunktionen können elektronisch überwacht werden. Signalspannungen werden
gemessen, gespeichert und auf Monitoren angezeigt (Amplitude und Zeitverlauf). Sie lernen einfache Analyseverfahren zur Signalauswertung mit dem Digitaloszilloskop kennen.
Aufgaben:
1. Nehmen Sie ein EKG (Elektrokardiogramm) über eine Serie von Pulsschlägen auf. Bestimmen
Sie aus der gegenseitigen Lage der R-Zacken die Pulsfrequenz. Berechnen Sie das Frequenzspektrum zu einer solchen Serie und lesen Sie die Pulsfrequenz ab.
2. Stellen Sie eine Periode des EKG gedehnt dar. Messen Sie die Zeitdauern des PQ-Intervalls, des
QRS-Komplexes und des QT-Intervalls. Vergleichen Sie Ihre Daten mit den Normalwerten.
3. Bestimmen Sie den Lagetyp (Lage der elektrischen Herzachse) aus den Amplitudenverhältnissen der R-Zacken in den Ableitungen nach Einthoven.
Grundlagen.:
Das Herz pumpt unentwegt Blut durch den Körper, so dass dieser mit Sauerstoff und lebenswichtigen Nährstoffen versorgt wird, andere Stoffe entsorgt werden. Der Herzmuskel zieht sich dabei
~70 Mal je Minute zusammen, 100000 Mal am Tag. Nach 70 Jahren hat das Herz etwa drei Milliarden Mal geschlagen, dabei ungefähr 180 Millionen Liter Blut bewegt. Gewöhnlich arbeitet das
Herz selbsttätig. Man spürt den eigenen Herzschlag nicht. Jedoch können äußere Umstände wie
sportliche Anstrengung, Aufregung, Freude und Angst das Herz vorübergehend in Fahrt bringen.
Das Wellen- und Zackenmuster des EKG zeigt die Ausbreitung der Erregung des Herzmuskels.
Die Erregungsleitung geht einher mit der Depolarisation der Membranen der Muskelzellen, was
als Potentialdifferenz sichtbar wird. Die Beziehung zwischen der Richtung der Ableitung dieses
elektrischen Potentials und der Richtung der Erregungsausbreitung legt fest, ob das entsprechende
Signal mit positivem oder negativem Ausschlag als Welle bzw. Zacke erscheint.
Herzrhythmus: Die Erregung des Herzmuskels beginnt gewöhnlich beim Sinusknoten (1). Die PWelle markiert die Erregungsausbreitung in den Vorhöfen [Anstieg:rechter Vorhof, Abfall: linker
Vorhof (2)]. Über den Atrioventrikularknoten durchtritt die Erregung verzögert (PQ-Zeit ~0,2 s)
das Herzskelett, eine elektrisch isolierende Schicht direkt über der Ventilebene zwischen Vorhöfen
und Kammern, und gelangt zur Kammermuskulatur, deren Erregung den QRS-Komplex ausbildet
(Dauer: < 0,12 s). Für die Dauer der ST-Strecke sind alle Muskelzellen depolarisiert (erregt), haben gleiches Potential. Dort zeigt das EKG also keinen Ausschlag (gesundes Herz). Die T-Welle
entsteht bei der Repolarisation der Kammerzellen (Rückbildung der Erregung). Dieser Vorgang
verläuft in anderer Reihenfolge als die Erregung und führt zu einem relativ breiten Ausschlag.
Das bei der Ausbreitung und Rückbildung der Erregung am Herzen entstehende elektrische Feld
greift bis zur Körperoberfläche aus. Entsprechende Potentialdifferenzen zwischen zwei Punkten
auf der Körperoberfläche werden als EKG registriert. Bei dieser extrazellulären Ableitung summieren sich die Potentialunterschiede zwischen erregten und ruhenden Muskelfasern. Vollständig
erregte bzw. ruhende Muskelmassen bewirken keine Potentialdifferenz.
38
Die durch die Muskeltätigkeit auftretenden Spannungen können mit Hilfe von zwei Elektroden,
die elektrischen Kontakt mit der Haut haben, gemessen werden (Einkanal-EKG). Störspannungen,
die durch elektrische und magnetische Felder in der Umgebung entstehen, sind häufig größer als
die zu messenden Körperpotentiale. Diese Störsignale sind aber auf allen Leitungen fast gleich. Zu
deren Beseitigung wird eine dritte (Referenz) Elektrode gelegt (schwarz). Die drei Messleitungen
werden einem Verstärker zugeführt, der nicht einfach nur verstärkt, sondern die Signale auch voneinander subtrahiert (Differenzverstärker). So erhält man die Spannungsdifferenz zwischen den
zwei Messpunkten (rot und gelb) weitgehend frei von Störsignale. Das entsprechende Ausgangssignal des Verstärkers wird dem Digitaloszilloskop zugeführt.
------------------------------------------------------------------------------------------------------------------
Rot
Gelb
Schwarz
Grün
Durchführung:
Der Verstärker (EKG-Box) wird mit Batterien (9V) betrieben, ist von der Netzspannung getrennt. Das Anlegen der Elektroden ist für Sie somit unbedenklich. Stellen Sie elektrischen Kontakt
mit Ihrem Körper mittels der Elektrodenbänder her. Befestigen Sie je ein Band an den Hand- bzw.
Fußgelenken. Die Frontseite der EKG-Box hat drei Buchsen. Schwarz wird mit dem rechten Bein
verbunden und dient als Referenzpunkt. Die zu untersuchende Potentialdifferenz wird zwischen
der roten und gelben Buchse abgeleitet. Nach Einthoven werden die Spannungen zwischen rechtem
und linkem Arm als Ableitung I, rechtem Arm und linkem Bein als Ableitung II sowie linkem Arm
und linkem Bein als Ableitung III bezeichnet /3,6/ (siehe Abb.).1 Eine grüne Buchse ist nicht vor1
Vergleichen Sie auch die Ableitungen nach Goldberger und Wilson /3,6/.
39
handen. Für die Ableitungen II und III müssen Sie die Buchsen rot/gelb mit den entsprechenden
anderen Messpunkten verbinden. An der Rückwand der EKG-Box sitzt ein T-Stück. Ausgehend
von hier werden die verstärkten Signale über Koaxialkabel auf die Kanäle 1 und 2 des Digitaloszilloskops geführt. Kanal 1 erhält das Wechselspannungssignal (AC). Auf Kanal 2 liegt das
Gleichspannungspotential (DC), das mit dem Potentiometer an der Vorderseite der EKG-Box intern auf Null zu regeln ist. Nach Überprüfung des Versuchsaufbaus durch den Betreuer schalten
Sie die EKG-Box ein (links beide Schalter – zur Kontrolle rote Lämpchen an der Vorderseite).
Das Rechnerprogramm Handyscope HS3 startet mit der Handyscope-Menueleiste, auf der Sie
den Transientenrecorder wählen. Der Versuchsbetreuer wird Sie im Einzelnen mit den Geräteeinstellungen und Messschritten vertraut machen. Einige wichtige bzw. empfohlene Parameter:
1) Messung: Kanäle 1 und 2
2) Kanal 1: Signalkopplung AC Empfindlichkeit 200 mV ggf. Softwareverstärkung erhöhen.
3) Kanal 2: Signalkopplung DC Empfindlichkeit 4 V ggf. Softwarespannungsversatz 2 V
4) Zeitbasis: 0.01/1000 (Zeitschritt in s/Werteanzahl - Das entspricht 10 s EKG-Aufzeichnung).
Sie stellen das Potentiometer der EKG-Box so ein, dass das Signal von Kanal 2 auf 0 V liegt.
Zu 1.: Sie messen das EKG nach Ableitung I. Wiederholen Sie die Messung, bis ein ungestörtes
Bild vorliegt. Warten Sie einen konstanten Herzrhythmus ab. Bei stets zu geringen oder untypischen Signalen wechseln Sie zur Ableitung II. Messen Sie den zeitlichen Abstand über mehrere
Perioden von R-Zacken hinweg. Nutzen Sie die Eingabemarken. Lesen Sie die Zeitdifferenz ab
und berechnen Sie die mittlere Zeit zwischen zwei benachbarten R-Zacken. Sie ist die Periodendauer des Herzrhythmus. Daraus berechnen Sie die Herzfrequenz bzw. den Puls.
Das Bild ist auszudrucken und die gemessenen Werte sind in die Grafik einzutragen.
Sie führen eine Spektrenanalyse durch. Dazu schalten Sie den Transientenrecorder aus und
starten das Oszilloskop. Alle zuvor eingestellten Parameter werden übernommen. Stellen Sie die
Zeitbasis auf sinnvolle Werte, z.B. 50.00S/sec. Schließlich starten Sie den Spektrumanalysator.
Stellen Sie Frequenzachse: Frequenzbereich 25.00 Hz. Beachten Sie, es wird nur die schon fertig
vermessene Pulssequenz nebst Frequenzspektrum angezeigt, während neue Daten im Hintergrund
auflaufen. Schieben Sie die Zeitnull der Pulssequenz auf den linken Bildrand.
Der Spektrumanalysator führt eine Transformation der Pulssequenz gemessen über der Zeitachse in eine Darstellung über der Frequenzachse durch. Hierbei wird die Pulssequenz als Überlagerung von Sinusfunktionen behandelt, deren Frequenzen im Spektrum erkennbar sind. Die deutliche Komponente bei der kleinsten Frequenz zeigt die Grundfrequenz (Frequenz ablesen - Puls).
Die spektralen Amplituden der Obertöne bei ganzzahligen Vielfachen der Grundfrequenz tragen
die Information über die Details der Pulsperiode bei regelmäßigem Herzrhythmus. Andere Spektrenanteile deuten auf arhythmische oder untypische Vorgänge hin.
Durch thermische Drift des Verstärkers kann es zu Problemen bei der Darstellung des Signals
kommen. Dann ist der Nullpunkt des Verstärkers (Kanal 2) nachzuregeln. Lassen Sie das ggf. von
Ihrem Betreuer ausführen.
Zu 2.: Die Messanordnung von 1. wird beibehalten. Gehen Sie zurück zum Transientenrecorder.
Registrieren Sie nun eine Periode in gedehnter Darstellung, z.B. durch Reduzierung der Anzahl der
Abtastpunkte auf 200 (Zeitbasis). Identifizieren Sie P-Welle, QRS-Komplex und T-Welle. Mit den
Eingabemarken können jetzt die gesuchten Zeitintervalle vermessen werden.
Drucken Sie das Bild aus. Markieren Sie P-Welle, QRS-Komplex und T-Welle. Tragen Sie die
gesuchten Intervalle ein. Geben Sie die gemssenen Zeiten an. Diskutieren Sie die Darstellung.
40
Zu 3.: Die vektorielle Auswertung des EKG erlaubt die annähernde Bestimmung der Herzlage im
Thorax mit der grafischen Darstellung der elektrischen Herzachse im Einthoven-Dreieck /4,6/.
Messen und drucken Sie die EKG-Ableitungen I, II und III (Zeitbasis 0.01/1000). Bestimmen Sie
für jede dieser Ableitungen die Spannung des R-Zacken bzgl. der Nulllinie. Nutzen Sie die Eingabemarken und wählen Sie Mittelwerte über eine Folge von Pulsperioden. Wählen Sie die Resultate
zweier Ableitungen aus und tragen Sie die Spannungswerte jeweils als Vektor mit entsprechender
Länge auf den Seiten des Einthoven-Dreiecks ab. Beachten Sie die Richtung der Ableitungen.
Zeichnen Sie senkrechte Linien in Anfangs- und Endpunkt der Vektoren. Die Verbindung vom
Dreiecksmittelpunkt zum Schnittpunkte der Linien ergibt den Vektor der elektrischen Herzachse.
Unter Umständen sind bestimmte Merkmale in Ihrem im Praktikum gemessenen EKG untypisch
ausgeprägt. Die EKG-Messungen erfolgen hier lediglich an Funktionsmustern von EKG-Geräten,
deren Resultate für die wirkliche medizinische Diagnostik ungeeignet sind.
Fragen:
1. Welcher Unterschied besteht zwischen Messung eines Aktionspotenzials und eines EKG?
2. Was versteht man unter der Richtung einer Ableitung?
3. Wie minimiert man messtechnisch die Störungen?
Literatur:
/1/ Beier/Pliquett: Physik für das Grundstudium Medizin
/2/ Glass: Physikalisches Praktikum
/3/ Schmidt: Physiologie kompakt, Springer-Verlag
/4/ Beier/Dörner: Die Physik und ihre Anwendungen in Medizin und Biologie (Bd.1)
/5/ Czech: Der Kathodenstrahloszillograph
/6/ www.grundkurs-ekg.de
41
10. γ-Strahlung / Tomographie und Bestrahlung
Ziele:
Eigenschaften und Messung der γ-Strahlung, Umgang mit Strahlungsquellen
Aufgaben:
1. Tomographische Lokalisierung eines metallischen Einschlusses in einem Holzwürfel.
2. Bestätigung des Absorptionsgesetzes, Bestimmung des Absorptionskoeffizienten eines Absorbermaterials (Pb) für γ-Strahlung einer bestimmten Photonenenergie (Radionuklid 137Cs).
3. Berechnung der Äquivalentdosis (Strahlenbelastung) für Ihre experimentelle Anordnung.
Grundlagen:
Zum Strahlenschutzes beim vorliegenden Versuch
1. Ausreichender Abstand ist bester Strahlenschutz. Bei einer Punktquelle nimmt die Strahlungsintensität umgekehrt proportional zum Quadrat des Abstandes von der Strahlungsquelle ab.
2. Strahlenbelastung proportional zur Aufenthaltsdauer, nicht unnötig in den Strahlenkegel fassen!
3. Schutz durch geeignete Abschirmung. Das radioaktive Material ist in einer metallischen Kapsel
dicht verschlossen. Die austretende γ-Strahlung wird durch einen Bleicontainer stark reduziert.
Achtung: Schwangere dürfen diesen Versuch nicht durchführen.
• γ-Strahlung
γ-Strahlung ist ebenso wie Röntgenstrahlung eine elektromagnetische Strahlung sehr kurzer
Wellenlänge bzw. hoher Photonenenergie. Entweder unterscheidet man beide Strahlungsarten
nach der Photonenenergie mit einer Trennlinie grob abgegrenzt bei 200 keV2 (Kiloelektronenvolt)
oder man unterscheidet nach der Herkunft der Strahlung: Röntgenstrahlung entsteht bei hochenergetischen Prozessen mit Elektronen und γ-Strahlung entsteht bei Prozessen in Atomkernen.
So gesehen besteht hinsichtlich der Photonenenergie ein großer Überlappungsbereich. Viele der
nachfolgend behandelten Eigenschaften, Anwendungen, Nachweismethoden, Betrachtungen zum
Strahlenschutz sind für beide Strahlungsarten relevant.
Nun weiter zur γ-Strahlung: Sie entsteht z.B. beim Zerfall natürlicher und künstlicher radioaktiver Nuklide. Häufig besitzen die Folgekerne kurzzeitig angeregte Zustände. Der Energieüberschuss bzgl. des Grundzustandes wird als elektromagnetische Strahlung (γ-Quanten) emittiert. Die
Photonenenergie dieser Strahlung ist charakteristisch für die betreffende Zerfallsreaktion. Als Beispiel sei der Zerfall des künstlichen Radionuklids 137Cs beschrieben, dessen γ-Strahlung im Praktikumsversuch eingesetzt wird. Die Kernreaktion ist ein β-Zerfall. Im 137Cs-Kern wird ein Neutron
zum Proton umgewandelt. Das austretende β--Teilchen (Elektron) hoher kinetischer Energie wird
im Metall der Kapsel, die die radioaktive Cäsiumverbindung umschließt, abgebremst und absorbiert. Beim Abbremsen entsteht Röntgenstrahlung, die ebenso die Ummantelung durchdringt wie
das γ-Quant (662 keV), das der angeregte Folgekern 137Ba* emittiert.
Der Nachweis der γ-Strahlung (Röntgenstrahlung) erfolgt über deren ionisierende Wirkung
in Materie. Dabei werden Elektronen aus Atomhüllen geschlagen, was mit vollständiger bzw. teilweiser Absorption der γ-Quanten einhergeht. Durch Abbremsen dieser Elektronen und Rekombination in den Atomhüllen entstehen energieärmere Röntgenquanten, die wiederum andere Elektronen
aus Atomhüllen lösen usw., bis alle γ-Energie in thermische Anregungen des Stoffes verwandelt ist
(abgesehen von strahleninduzierten molekularen Reaktionen, in die ggf. ein kleiner Energieanteil
deponiert wird). Die Kaskade der genannten Reaktionen läuft in sehr kurzer Zeit ab, in weniger als
einer Mikrosekunde, und wird deshalb als Einschlag eines einzigen γ-Quants registriert.
2 Die kinetische Energie eines freien Elektrons ändert sich um 1 eV = 1,602 · 10-19 J, wenn es eine Spannung
von 1 V durchläuft.
42
• Aufbau und Wirkungsweise der Messapparatur
Beim Praktikumsversuch wird ein Szintillationszähler zum γ-Nachweis eingesetzt, wie er auch
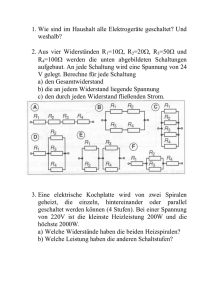
in der Nuklearmedizin bekannt ist. Der Szintillationszähler (Abb. 10-1) besteht aus einem besonderen Kristall, dem Szintillatorkristall (1): z.B. Natriumiodid dotiert mit Thallium, Lichtleiter (2),
Photokathode (3), Sekundärelektronenvervielfacher (SEV) (4,5) und Vorverstärker. Im Szintillatorkristall führen oben genannte Anregungen zur Emission von Photonen sichtbaren Lichts. Die
mit der Absorption eines γ-Quants von z.B. Eγ = 1 MeV verbundenen Prozesse können ca. 30000
Lichtquanten (Photonen) erzeugen. Die auf die Photokathode gelangten Photonen lösen durch den
lichtelektrischen Effekt Elektronen aus. Deren Zahl wird an den Dynoden (4) des SEV vergrößert.
Bei einem von der Photokathode ausgehenden Elektron erreichen ca. 106 ... 108 Elektronen die
Anode (5) des SEV. Der Grad der Vervielfachung, die Verstärkung des SEV, steigt mit wachsender Spannung zwischen den Dynoden an. So kann ein γ-Quant mit Eγ = 1 MeV die Ladungsmenge
von 1010 ... 1012 Elektronen an der Anode des SEV erzeugen. Diese Ladung fließt durch den Arbeitswiderstand R ab, was beim Verstärker als Spannungsimpuls registriert wird.
Abb. 10-1. Aufbau eines Szintillationszählers
1 – Szintillator; 2 – Lichtleiter; 3 – Photokathode; 4 – Dynoden; 5 – Anode; 6 – Reflektor;
7 – lichtdichtes Gehäuse; 8 – Spannungsteiler [W. STOLZ, Radioaktivität ... 1996, S. 124]
Entsprechend der beschriebenen Funktionsweise ist die Amplitude des Spannungspulses proportional zur Energie, die vom einfallenden γ-Quant absorbiert wurde. Die Impulshöhe kann deshalb
zur Bestimmung der γ-Energie und damit zur Identifizierung der Zerfallsreaktion bzw. des Radionuklids genutzt werden. Das entsprechende γ-Spektrometer besteht aus dem eben beschriebenen
Szintillationszähler sowie dem PC-Einschub, in dem Linearverstärker, Spannungsquelle für den
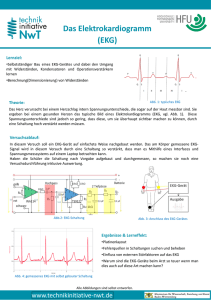
SEV, Diskriminator, Vielkanalanalysator, Zähl- und Vorwahlprogramme vereint sind. Beim Vielkanalanalysator (MCA) werden die Impulse entsprechend der Impulshöhe den Kanälen zugeordnet und gezählt. Abb. 10-2 zeigt das für eine 137Cs-Quelle typische Spektrum. Die ursprüngliche
1500
1200
Cs
Plateau
1000
1000
500
800
Arbeitsspannung UA
bei 662 keV
Impulszahl Z
Impulszahl Z
Photopeak
137
600
400
200
0
Energiefenster
0
500
1000
MCA-Kanal
1500
0
300
2000
400
500
600
700
800
900
SEV-Spannung U/V
Abb. 10-2. γ-Spektrum einer 137Cs-Quelle
Abb. 10-3. Kennlinie einer Messsonde
43
Photolinie wäre nur wenige Zählkanäle breit, aber die Prozesse im Szintillationszähler sind vielen
Zufällen unterworfen. Daher werden die Höhen der Spannungspulse den absorbierten γ-Energien
nur unscharf zugeordnet, d.h., die γ-Photolinie wird schlecht aufgelöst. Neben dem genannten Peak
beim Kanal 1550, der die vollständige Absorption des γ-Quants von 662 keV anzeigt, gibt es noch
einen großen Anteil an Impulsen bei Zählkanälen deutlich geringerer Photonenenergien. Diese
Zählereignisse gehören zu unvollständig absorbierten γ-Quanten oder der Röntgenbremsstrahlung
der β-Teilchen. Ein Spektrum wie in Abb. 10-2 wird im Analysatorbetrieb aufgenommen.
Bei den Start/Stopp-Messungen mit Diskriminatorbetrieb, die Sie verwenden, wird der genutzte Bereich der Zählkanäle eingegrenzt. Dabei werden alle Ereignisse gezählt, die im eingestellten Energiefenster liegen. Sie wählen ein Energiefenster um den Photopeak, um nur γ-Quanten
mit Energien von 662 keV zuzulassen und alle anderen Photonen auszuschliessen.
Mit Vorwahl wird bei Start/ Stopp-Messungen entweder eine bestimmte Impulszahl (i) oder
eine bestimmte Zählzeit (ii) vorgegeben, nach deren Erreichen die Zählung beendet ist. Das entsprechende Resultat ist dann entweder eine Messzeit (i) oder eine Impulszahl (ii).
Variiert man bei konstanter Verstärkung und weit offenem Energiefenster die Hochspannung,
so erhält man die Kennlinie des Szintillationszählers wie z.B. in Abb. 10-3 gezeigt. Im Plateaubereich werden alle Ereignisse im SEV hinreichend verstärkt, um gezählt werden zu können.
Thermisches Rauschen ist noch weitgehend unterdrückt. Die für den SEV verwendete Spannung
(Arbeitspunkt UA) liegt in der Mitte des Plateaus. Jegliche Drift der Verstärkung und Hochspannung soll die Messung nicht stören. Andere Messwertschwankungen sind auf das natürliche Maß
des Zufalls der Zerfalls- und Nachweisreaktionen beschränkt. Bei stets gleicher Messzeit erhalten
Sie variierende Impulszahlen Z mit einer Gaussverteilung um Z mit Standardabweichung Z .
An Ihrem Messplatz (Nummer beachten) liegen benötigte Messplatzparameter aus: die Dicken
der Bleiplatten, das γ-Spektrum 137Cs und die Hochspannungskennlinie.
• Schwächung von γ-Strahlung
Für die Änderung der Intensität I der γ-Strahlung beim Durchgang durch stoffliche Materie gilt
allgemein das Absorptionsgesetz mit einer exponentiellen Abnahme der Intensität
I = I0 e− µ X
(10.1)
mit
I
–
Intensität (γ-Quanten je Zeiteinheit) der bei der Dicke X der durchstrahlten Schicht austretenden Strahlung,
I0
–
Intensität der in die Schicht eintretenden Strahlung (X = 0 mm),
µ
–
Absorptionskoeffizient des Materials (Einheit z.B. [µ] = mm–1).
Der Absorptionskoeffizient µ hängt sowohl von der Dichte und den Bindungszuständen der Elektronen des Absorbermaterials als auch von der Energie der einfallenden γ-Quanten ab.
Den Messwerten I ist stets ein Nulleffekt Inull überlagert. Inull ist die Impulsrate ohne Präparat,
die durch kosmische Strahlung, terrestrische Umgebungsstrahlung und vom Szintillationszähler
selbst bewirkt wird. Inull ist von den Messwerten I, I0 vor der weiteren Auswertung abzuziehen.
Zur Ermittlung von µ wird Gleichung (10.1) mit [ I ] = s-1 dividiert und logarithmiert:
ln{ I } = ln{I 0 } − µ ⋅ X
(10.2)
Jetzt wird ein Koeffizientenvergleich von (10.2) mit einer Geradengleichung der Form
y = b + a⋅x
(10.3)
durchgeführt. Aus der linearen Regression folgt wegen der Analogie von (10.2) und (10.3) für
den Anstieg der Geraden a = –µ und für die Schichtdicke X = 0 folgt b = ln { I0 }.
Das Transmissionsvermögen T(X) einer Schicht der Dicke X definiert den Teil der Strahlung,
der nicht absorbiert wird. Mit Gleichung (10.1) folgt
(10.4)
T(X) = I(X) / I0 = e –µ X .
Das Absorptionsvermögen A(X) ist der absorbierte Teil mit A(X) = 1 – T(X).
44
• Begriffe der Dosimetrie
Strahlung (γ-Strahlung, Röntgenstrahlung) kann nur dann Wirkungen hervorrufen, wenn ihre
Wechselwirkung eine Energieübertragung auf das durchstrahlte Material vollzieht. Wichtig zur
Charakterisierung dieser Strahlenwirkung sind folgende Größen:
D = ∆E / ∆m ,
a) Die Energiedosis D,
(10.5)
ist die von einem Stoff der Masse ∆m absorbierte Energie ∆E. Die Einheit der Energiedosis ist
J/kg = Gy (Gray).
P = dD / dt = ∆E / (∆m ⋅ ∆t ) ,
b) Die Energiedosisleistung P,
(10.6)
gibt die Energie an, die von der Masseneinheit pro Zeiteinheit absorbiert wird. Die Einheit der
Energiedosisleistung ist J/(kg⋅s) = Gy/s.
c) Die Äquivalentdosis H wurde im Rahmen des Strahlenschutzes zur Kennzeichnung der biologischen Wirksamkeit und zur Beurteilung des ungleichen Strahlenrisikos durch verschiedene
H = wR ⋅ D .
Strahlungsarten eingeführt. Es gilt der Zusammenhang
(10.7)
Dabei ist wR ein dimensionsloser Strahlenwichtungsfaktor, der von der Strahlungsart (α-Teilchen,
thermische Neutronen, β- und γ-Strahlung) abhängt:
wα = 20,
wn = 5,
wβ = wγ = 1 .
(10.8)
Die Einheit der Äquivalentdosis ist J/kg = Sv (Sievert).
In der Strahlenschutzverordnung der Bundesrepublik Deutschland sind Grenzwerte der Äquivalentdosis angegeben. Für beliebige Personen beträgt der Grenzwert der Dosis beim Umgang mit
Quellen ionisierender Strahlung 1 mSv je Kalenderjahr (allg. ohne die unterschiedliche Empfindlichkeit verschiedener Organe zu berücksichtigen). Für Personen im betrieblichen Überwachungsbereich gilt, dass durch die Verwendung radioaktiver Stoffe und den Betrieb radioaktiver Anlagen
die von einer Person aufgenommene Dosis 20 mSv je Jahr nicht überschreiten darf. Zum Vergleich: Die durchschnittliche Äquivalentdosis durch Höhenstrahlung, terrestrische Strahlung, inkorporierte radioaktive Stoffe und medizinische Vorsorge beträgt in Deutschland ~3,3 mSv je
Jahr insgesamt.
Die Berechnung der Äquivalentdosis, die hier im Praktikum vorgenommen wird, nutzt folgende
Zusammenhänge: Eine unabgeschirmte punktförmige γ-Strahlungsquelle der Aktivität A erzeugt
im Abstand r in einem Zeitintervall ∆t im menschlichen Organismus die Äquivalentdosis
A
∆H = Γ 2 ∆t .
(10.9)
r
Die Dosisleistungskonstante Γ ist energieabhängig. Entsprechende Werte für ausgewählte Radionuklide sind in Tab. 10-1 gegeben.
Die augenblickliche Aktivität A(t) eines Präparats kann mit dem Zerfallsgesetz
−
t
ln 2
A = A0 ⋅ e – λ t = A0 ⋅ e T
(10.10)
berechnet werden, wenn zu einem bestimmten Zeitpunkt die Aktivität bekannt war, mit
A0
–
Aktivität des Präparats am Herstellungstag,
λ = ln2 /T
–
Umwandlungskonstante des Nuklids,
T
–
Halbwertszeit (Tab. 10-1),
t
–
Zeit seit der Herstellung/Vermessung des Präparats.
Aktivität bezeichnet Zerfälle je Zeiteinheit mit der Maßeinheit [ A ] = s-1 = Bq (Becquerel).
Tab. 10-1. Halbwertszeiten und Dosisleistungskonstanten einiger Radionuklide (DIN 6844-3)
Radionuklid
22
Na
60
Co
137
Cs
Halbwertszeit /a
2,603
5,272
30,17
45
Γ / [ µSv · m2 / (h · MBq)]
0,333
0,354
0,0927
Durchführung
Die Messungen werden über ein PC-Programm gesteuert. Das Programm ist gestartet und der
Messplatz betriebsbereit. Unter der Spalte Messungen wählen Sie "Start/Stop-Messung". Kontrollieren Sie rechts die eingestellten Parameter Verstärkung (20.0), Analysatorpegel Funten, Foben
(siehe γ-Spektrum 137Cs an Ihrem Messplatz ausliegend) und unten rechts Ist - Hochspannung
(siehe Kennlinie ebenfalls ausliegend). Bei Problemen bitte an den Versuchsbetreuer wenden!
Vom Betreuer erhalten Sie ein 137Cs-Präparat bzw. es steht schon an Ihrem Messplatz. Es sollte
die Nummer Ihres Messplatzes tragen. Den Bleibehälter mit Präparat stellen Sie unter die Messsonde und nehmen den Bleideckel ab.
Zu 1.: Tomographie
Bestimmen Sie die Lage eines metallischen Einschlusses in einem Holzwürfel durch Ausnutzung
des unterschiedlichen Absorptionsvermögens der Materialien für γ-Strahlung (einfaches Beispiel
eines tomographischen Verfahrens). Dazu legen Sie die kreisrunde Plastikscheibe auf den Bleibehälter, so dass der Rand in die Nut der Scheibe fasst. Der Bleibehälter steht in der Mitte unter der
Messsonde. Positionieren Sie den Holzwürfel mit seinen Flächen A – D und 1 – 4 nacheinander
auf der Markierung und messen Sie jeweils die Impulszahl Z bei Zeitvorwahl (günstige Messzeit
t = 60 s) ohne andere Messbedingungen zu verändern.
Überprüfen Sie für eine der sechs hohen und eine der zwei niedrigen Impulszahlen, ob die Verminderung der gemessenen Impulszahlen durch den metallischen Einschluss signifikant ist, d.h.
größer als beide Messunsicherheiten. Die absolute Messunsicherheit uz einer Impulszahl Z ist mit
u Z = 2 Z für einen Vertrauensbereich P = 95% gegeben.
Erstellen Sie eine Grafik der acht Messwerte und tragen Sie die beiden Intervalle (hoch, niedrig)
der Messunsicherheit [Z – uZ, Z + uZ] in die Grafik ein.
Zu 2.: Absorptionskoeffizient µ eines Absorbers (Pb)
Stellen Sie das radioaktive Präparat (ohne Deckel) möglichst nahe an die Sonde (ggf. Holzwürfel
darunter stellen), aber der Stapel Bleiplatten muss noch zwischen Präparat und Sonde passen.
Sie nutzen Impulsvorwahl, um die Messunsicherheit für alle Schichtdicken konstant zu halten.
Eine Impulszahl von Z = 10000 ist optimal (ohne Absorberschicht). Starten Sie eine Testmessung.
Falls die vorgewählte Impulszahl eine Messzeit deutlich unter oder über 60 s ergibt, ändern Sie
die vorgewählte Impulszahl entsprechend.
Jetzt starten Sie die Messserie. Die Zählzeit t ist in Abhängigkeit von der Dicke X des Stapels
Bleiplatten zu messen. Die erste Messung erfolgt ohne Bleiplatten. Bei den weiteren Messungen
werden auf das radioaktive Präparat nacheinander Bleiplatten dazugelegt, so dass sich die Stapelhöhe bei jeder weiteren Messung um eine Platte vergrößert. Die Zeit t wird zunehmend größer.
Zur Bestimmung des Nulleffekts Inull nutzen Sie die Messzeit des größten Plattenstapels (Umschalten auf Zeitvorwahl). Das Präparat wird dazu weit entfernt von der Szintillationssonde mit
Deckel verschlossen abgestellt. Alle erhaltenen Messwerte sind zu protokollieren.
Zweckmäßig für die Messserie ist folgende Tabelle
Platten-Nr.
xi / mm
X / mm
Z
0
0
0
ca. 10000
t/s
I / s-1
(I – Inull) / s-1
mit den Impulsraten I = Z/t.
Die Bestimmung von µ erfolgt mit einer Ausgleichsgeraden. Zu deren Berechnung nutzen Sie
ein Computerprogramm, das Ihnen mittels linearer Regression aus den Werten ln{(I – Inull)/s–1} als
Funktion von X gemäß Gl. (10.2) den Anstieg der optimalen Geraden liefert (Eingabe Wertepaare
(I – Inull)/s–1 und X ). Das Logarithmieren erfolgt direkt im Programm als Achsentransformation.
46
Vervollständigen Sie die Angaben und drucken Sie die Grafik aus. Neben dem Anstieg a = –µ
erhalten Sie dessen relative und absolute Fehler mit einer statistischen Sicherheit von P = 95 %.
Die Auswertung dieses Versuchsteils berücksichtigt folgende Punkte:
• Formulieren Sie das Messergebnis.
• Vergleichen Sie mit dem Literaturwert. Liegt dieser im Intervall Ihrer Messunsicherheit [µ – uµ ,
µ + uµ]? Diskutieren Sie ggf. die Abweichungen.
• Zeigt die logarithm. Kurve lineares Verhalten wie nach dem Absorptionsgesetz zu erwarten?
Akzeptierte Werte für die Absorptionskoeffizienten bei Eγ = 0,662 MeV (137Cs) /2/ sind:
µAl = 0,020 mm-1
µFe = 0,058 mm-1
µPb = 0,120 mm-1
Zu 3.: Äquivalentdosis
1. Berechnen Sie die aktuelle Aktivität des von Ihnen verwendeten Präparats nach Gl. (10.10).
2. Welche Äquivalentdosis würden Sie nach Gl. (10.9) erhalten, falls Sie ohne Abschirmung
durch den Bleibehälter zwei Stunden in 0,5 m Abstand vor Ihrem 137Cs-Präparat sitzen?
3. Wie reduziert sich die Äquivalentdosis, wenn Sie den Bleibehälter berücksichtigen? Nutzen Sie
Ihren Messwert des Absorptionskoeffizienten µ zur Berechnung des Transmissionsvermögens
T(X) nach Gleichung (10.4). Die Wandstärke des Bleibehälters ist 2,4 cm.
4. Beurteilen Sie den erhaltenen Wert. Vergleichen Sie mit den zulässigen Grenzwerten. Ist das
Weglassen zusätzlicher Abschirmungen gerechtfertigt?
5. Vergleichen Sie das Absorptionsvermögen des Metalls Blei mit dem von Fe und Al. Welches
Material ist für Strahlenschutzmaßnahmen (γ-Strahlung) besonders geeignet?
Fragen, Aufgaben:
1. Was sind γ-Strahlen und wie entstehen sie?
2. Warum kann man aus der Lage der Photolinien den γ-Strahler bestimmen?
3. Welche wesentlichen Teile enthält das verwendete γ-Spektrometer?
4. Was ist die Wechselwirkung zwischen γ-Strahlung und Materie?
5. Wie lautet das Absorptionsgesetz für γ-Strahlen?
6. Was sind die Ursachen des Nulleffekts bei kernphysikalischen Messungen?
7. Was versteht man unter der Aktivität eines radioaktiven Stoffes und wie ist das entsprechende
zeitliche Verhalten der Aktivität?
8. Nennen Sie einige für die Medizin wichtige Radionuklide und geben Sie die wichtigsten Kenndaten für diese an!
9. Was versteht man unter den Begriffen Energiedosis und Äquivalentdosis? In welchen Einheiten
werden diese Größen angegeben?
10. Begründen Sie die höhere biologische Strahlenwirksamkeit von α-Strahlung im Vergleich zur
γ-Strahlung!
Literatur:
/1/ J. VAN CALKER, H.-R. KLEINHANß: Physikalisches Kurspraktikum für Mediziner und
Naturwissenschaftler; Stuttgart, 3. Aufl. 1989
/2/ L. HERFORTH, H. KOCH: Praktikum der Radioaktivität und Radiochemie
(bearb. K. HÜBNER); Leipzig, 3. Aufl. 1992
/3/ H. R. MÜLLER, R. GRÄFE, D. FALKENHAGEN: Grundriss der Physik für Mediziner und
medizinische Berufe; Thun, 4. Aufl. 1990
/4/ Physikalisches Praktikum, mit multimedialen Ergänzungen
(hrsg. D. GESCHKE, bearb. H. ERNST, begr. W. ILBERG); Stuttgart, 12. Aufl. 2001
/5/ W. STOLZ: Radioaktivität – Grundlagen, Messung, Anwendungen; Stuttgart, 3. Aufl. 1996
47