M 2016-4 r r r r r r Erklärung der Lösung: Ein Quadrat hat 4 gleich

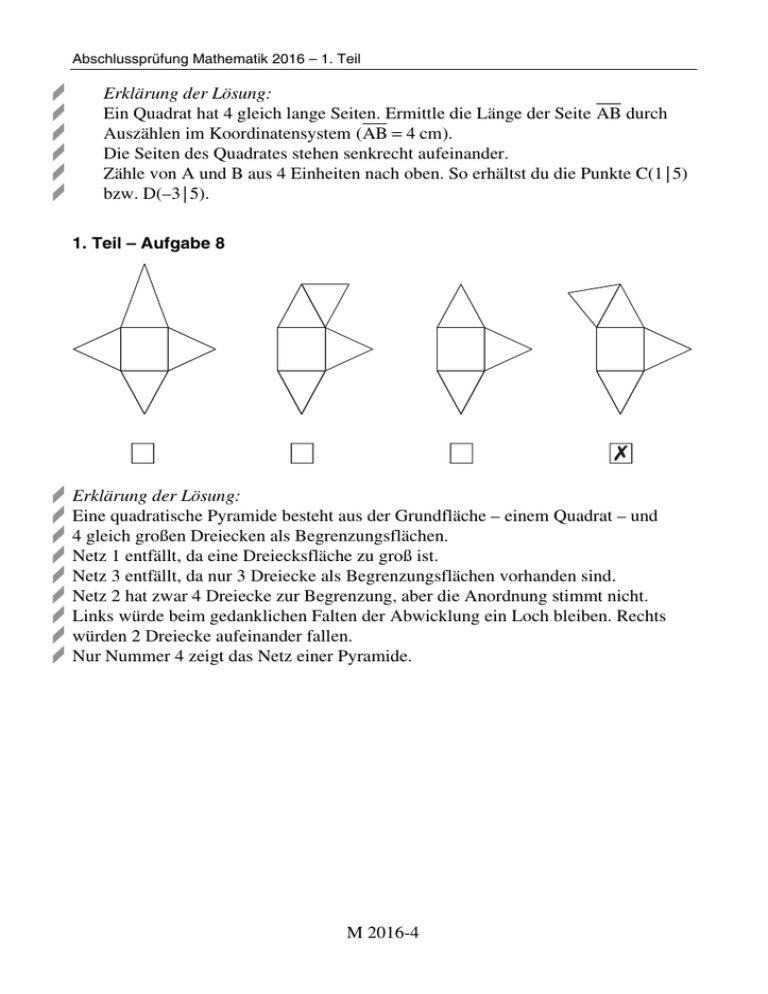
Abschlussprüfung Mathematik 2016 – 1. Teil
r
r
r
r
r
r
Erklärung der Lösung:
Ein Quadrat hat 4 gleich lange Seiten. Ermittle die Länge der Seite AB durch
Auszählen im Koordinatensystem (AB = 4 cm).
Die Seiten des Quadrates stehen senkrecht aufeinander.
Zähle von A und B aus 4 Einheiten nach oben. So erhältst du die Punkte C(1 | 5)
bzw. D(–3 | 5).
1. Teil – Aufgabe 8
r
r
r
r
r
r
r
r
r
Erklärung der Lösung:
Eine quadratische Pyramide besteht aus der Grundfläche – einem Quadrat – und
4 gleich großen Dreiecken als Begrenzungsflächen.
Netz 1 entfällt, da eine Dreiecksfläche zu groß ist.
Netz 3 entfällt, da nur 3 Dreiecke als Begrenzungsflächen vorhanden sind.
Netz 2 hat zwar 4 Dreiecke zur Begrenzung, aber die Anordnung stimmt nicht.
Links würde beim gedanklichen Falten der Abwicklung ein Loch bleiben. Rechts
würden 2 Dreiecke aufeinander fallen.
Nur Nummer 4 zeigt das Netz einer Pyramide.
M 2016-4
Abschlussprüfung Mathematik 2016 – 2. Teil
2. Teil (mit Taschenrechner)
Lösungs-Tipps zum 2. Teil
Die folgenden Tipps verraten dir schrittweise einen möglichen Lösungsweg. Lies
also den zweiten Tipp erst, wenn du mit dem vorherigen nicht weitergekommen bist.
Tipps zu Aufgabe 9
r Suche aus dem Angebot die Einzelpreise heraus und addiere diese.
r Bestimme dann aus dem Gesamtwert die Liefergebühr für die Bestellung.
Tipps zu Aufgabe 10
a)
r Zeichne die Strecke AC = 7,5 cm (lange Diagonale).
r Zeichne die Strecke BD = 6 cm (kurze Diagonale) im Abstand von 2 cm zu Punkt C.
r Beachte dabei: Die Diagonalen stehen senkrecht aufeinander, die lange Diagonale
halbiert die kurze Diagonale.
r Verbinde die Enden der Diagonalen zum Drachenviereck und beschrifte die
Eckpunkte.
r Achte beim Zeichnen auf Genauigkeit.
b)
r Schreibe zuerst die Formel für den Flächeninhalt eines Drachenvierecks auf.
r Bestimme dann die Längen der Diagonalen e = AC und f = BD.
r Vergiss die Maßeinheiten nicht.
Tipps zu Aufgabe 11
a)
r Fasse auf der rechten Seite der Gleichung alle Glieder ohne Variable zusammen.
r Ordne, indem du alle Glieder mit Variable nach links und alle Glieder ohne Variable
nach rechts bringst.
r Isoliere die Variable.
b)
r Setze in den Term für x und y die gegebenen Zahlen ein und berechne dann.
Tipps zu Aufgabe 12
a)
r Subtrahiere von 100 % die Prozentsätze, die für Möbel und für den Schulgarten
ausgegeben werden.
M 2016-5
Abschlussprüfung Mathematik 2016 – 2. Teil
b)
r Berechne mit dem Dreisatz 45 % von 6 000 e.
c)
r Überlege, welche Fläche die einzelnen Prozentsätze ungefähr in einem Kreisdiagramm einnehmen müssen.
r Für neue Möbel werden 45 % des Geldes ausgegeben. Das ist fast die Hälfte. Damit
entfallen die Diagramme B und C, da die schwarze Fläche mehr als die Hälfte
einnimmt.
r 25 % des Geldes werden für Spielgeräte ausgegeben. Das ist ein Viertel des Geldes.
Kreisdiagramm D entfällt also auch, da keine Fläche ein Viertel darstellt.
Tipps zu Aufgabe 13
a)
r Die Volumenformel für den Zylinder lautet V = π ⋅ r 2 ⋅ h k .
r Gib das Volumen in Litern an (1 dm 3 = 1 000 cm 3 ; 1 dm 3 1 ).
b)
r Überlege mithilfe der Volumenformel des Zylinders, welcher Zusammenhang
zwischen Radius und Volumen besteht.
r Beachte, dass der Radius quadratisch in die Rechnung eingeht.
Tipps zu Aufgabe 14
r Überprüfe, ob der Satz des Pythagoras c2 = a2 + b2 gilt.
r c wäre dann die Hypotenuse, also die Seite, die dem rechten Winkel gegenüberliegt.
r a und b wären die Katheten, also die Seiten, die den rechten Winkel einschließen.
Tipps zu Aufgabe 15
a)
r 1. Auf einem Feld von 10 gleich großen Feldern steht die Zahl 5.
r 2. Kleiner als 7 sind 1, 2, 3, 4, 5 und 6. Also sind 6 von 10 Zahlen kleiner als 7.
b)
1 .
r Die Wahrscheinlichkeit für die Zahl 3 beträgt 10
r Bei einem mehrstufigen Zufallsexperiment müssen die Wahrscheinlichkeiten
multipliziert werden (Pfadregel).
M 2016-6