BGYW 2016 a – VWL – 3.2.1
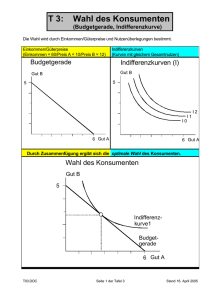
Werbung
3.2.1 Bilanzgerade, Indifferenzkurve und Haushaltsoptimum VOLKSWIRTSCHAFTSLEHRE © SEI Klasse: __________ Datum: ___________ Thema: Haushaltsoptimum Arbeitsauftrag Bearbeiten Sie die folgenden Aufgaben und Fragen zu Hause! Fragen lesen Fragen beantworten schriftlich Partnerarbeit Hausaufgabe 1. Was gibt die Indifferenzkurve an? _________________________________________________ ____________________________________________________________________________ 2. Was gibt die Budgetgerade an? __________________________________________________ ____________________________________________________________________________ 3. Einem Haushalt stehen von seinem Einkommen 1000,00 € für Konsumzwecke zur Verfügung (YC). Etwaiges Sparen und Ausgaben für Steuern und Versicherungen sind hierbei bereits abgezogen. Es gilt die Annahme, dass der Haushalt nur an zwei Gütern interessiert ist: Gut x und Gut y. Der Preis für Gut x (px) beträgt je Stück 25,00 €, der Preis für Gut y (p y) je Stück 20,00 €. Errechnen Sie, welche Mengen der beiden Güter der Haushalt im Extremfalle erwirbt und zeichnen Sie die Budgetgerade in das Koordinatensystem auf der folgenden Seite. px in € x py in € 25,00 20,00 25,00 20,00 y Ausgaben- Ausgabensumme für summe für Gut x in € Gut y in € Konsumsumme (YC) in € 4. Dem Haushalt stehen für die beiden Güter x und y die folgenden Güterkombinationen zur Auswahl, zwischen welchen er gleichgültig ist. Tragen Sie die Werte im Koordinatensystem ab, und verbinden Sie die Punkte zur Indifferenzkurve. Bezeichnen Sie diese mit I1. Güterkombinationen A B C Gut x 35 24 15 Gut y 10 20 40 Gesamtnutzen UK1 UK1 UK1 5. Der Berührungspunkt zwischen Budgetgerade und Indifferenzkurve gibt das Haushaltsoptimum, also den optimalen Verbrauchsplan an. Welche Bedingungen muss dieses Haushaltsoptimum erfüllen? Ziehen Sie die Erkenntnisse aus dem erstellten Schaubild zur Beantwortung dieser Frage heran. (1) _________________________________________________________________________ (2) _________________________________________________________________________ 1 3.2.1 Bilanzgerade, Indifferenzkurve und Haushaltsoptimum 6. Zeichnen Sie die beiden Indifferenzkurven, für welche die folgenden Güterkombinationen gelten. Bezeichnen Sie diese mit I2 und I3. Güterkombinationen der Indifferenzkurve I2 A B C Güterkombinationen der Indifferenzkurve I3 A B C Gut x 27 19 11 44 31 20 Gut y 10 20 40 10 20 40 Gesamtnutzen UK2 UK2 UK2 UK3 UK3 UK3 7. Welche Aussage lässt sich machen über Indifferenzkurven, die (a) unterhalb der Budgetgeraden liegen? _________________________________________________________________________ (b) oberhalb der Budgetgeraden liegen? _________________________________________________________________________ 8. Zeichnen Sie zwei weitere Budgetgeraden ein, die parallel zur bereits vorhandenen sind und die die Indifferenzkurven I2 und I3 berühren. Was passiert bei einem höheren Einkommen? ____________________________________________________________________________ ____________________________________________________________________________ 2 Gut y 50 10 Gut x 10 50