Grundlagen der Wahrscheinlichkeitsrechnung Aufgaben und
Werbung
Prof. Dr. W. Schmitt | Leistungsanalyse & -bewertung …
4. November 2011
Grundlagen der Wahrscheinlichkeitsrechnung
Aufgaben und Fragen zur Lernkontrolle - Lösungen
Aufgabe 1 (Ergebnis- und Ereignisraum)
04. Nov. 2011
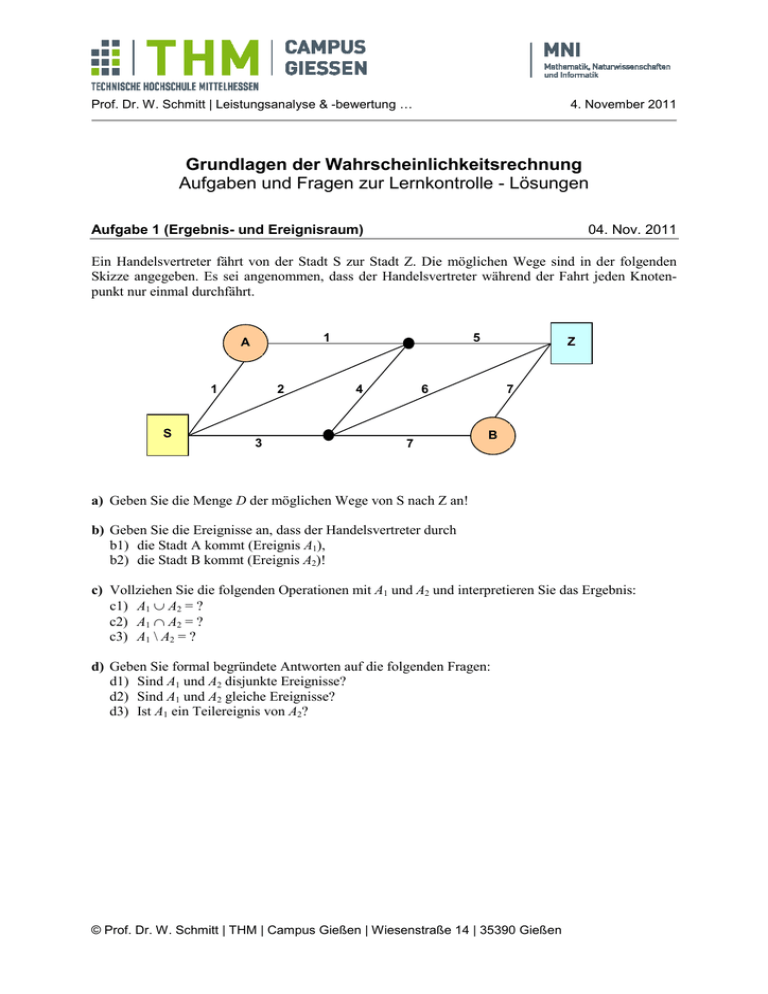
Ein Handelsvertreter fährt von der Stadt S zur Stadt Z. Die möglichen Wege sind in der folgenden
Skizze angegeben. Es sei angenommen, dass der Handelsvertreter während der Fahrt jeden Knotenpunkt nur einmal durchfährt.
1
S
5
1
A
2
3
4
Z
6
7
7
B
a) Geben Sie die Menge D der möglichen Wege von S nach Z an!
b) Geben Sie die Ereignisse an, dass der Handelsvertreter durch
b1) die Stadt A kommt (Ereignis A1),
b2) die Stadt B kommt (Ereignis A2)!
c) Vollziehen Sie die folgenden Operationen mit A1 und A2 und interpretieren Sie das Ergebnis:
c1) A1 ∪ A2 = ?
c2) A1 ∩ A2 = ?
c3) A1 \ A2 = ?
d) Geben Sie formal begründete Antworten auf die folgenden Fragen:
d1) Sind A1 und A2 disjunkte Ereignisse?
d2) Sind A1 und A2 gleiche Ereignisse?
d3) Ist A1 ein Teilereignis von A2?
© Prof. Dr. W. Schmitt | THM | Campus Gießen | Wiesenstraße 14 | 35390 Gießen
2
Aufgabe 2 (Symmetrischer Würfel und Abzählregel)
04. Nov. 2011
Es werde mit einem symmetrischen Würfel zweimal geworfen. Zwei Ereignisse A, B seien wie folgt
definiert:
A: Augensumme gerade.
B: 4 < Augensumme < 8.
a)
Vervollständigen sie das folgende Venn-Diagramm für den Ergebnisraum Ω, indem Sie die Ereignismengen A und B markieren!
Ω
(1, 1)
(1, 2)
(1, 3)
(1, 4)
(1, 5)
(1, 6)
(2, 1)
(2, 2)
(2, 3)
(2, 4)
(2, 5)
(2, 6)
(3, 1)
(3, 2)
(3, 3)
(3, 4)
(3, 5)
(3, 6)
(4, 1)
(4, 2)
(4, 3)
(4, 4)
(4, 5)
(4, 6)
(5, 1)
(5, 2)
(5, 3)
(5, 4)
(5, 5)
(5, 6)
(6, 1)
(6, 2)
(6, 3)
(6, 4)
(6, 5)
(6, 6)
Ergebnis 1. Wurf
Ergebnis 2. Wurf
(x, y)
b) Berechnen Sie die Wahrscheinlichkeiten für das Eintreten der folgenden Ereignisse:
A, B , A ∩ B, A ∪ B, A ∩ B sowie A ∪ B !
c) Sind die Ereignisse A und B unabhängig voneinander? Begründen Sie Ihre Antwort mathematisch!
Aufgabe 3 (Bedingte Wahrscheinlichkeit)
04. Nov. 2011
Ein Drogenspürhund zeigt durch Bellen an, wenn er meint Rauschgift zu riechen. Durch statistische
Messungen bei der Zollkontrolle hat man herausgefunden, dass in 93% der Fälle, in denen der Hund
bellt, die Ladung tatsächlich Rauschgift enthält. Bei 7% der Kontrollen bellt der Hund jedoch, obwohl
kein Rauschgift vorhanden ist. Schließlich hat man herausgefunden, dass in einer von 1000 kontrollierten Ladungen Rauschgift versteckt ist.
a) Wie groß ist die Wahrscheinlichkeit, dass bei der Kontrolle einer Ladung der Spürhund bellt?
b) Wie groß ist die Wahrscheinlichkeit, dass eine Ladung, bei der der Hund bellt, auch tatsächlich
Rauschgift enthält?
© Prof. Dr. W. Schmitt | Leistungsanalyse & -bewertung …| Wahrscheinlichkeitsrechnung
3
Aufgabe 4 (Diskrete Zufallsvariable)
25. Okt. 2011
Drei Systeme S1, S2 und S3 sind in einem bestimmten Zeitraum unabhängig voneinander mit den
folgenden Wahrscheinlichkeiten defekt:
P({S1 defekt}) = 0,1
P({S2 defekt}) = 0,2
P({S3 defekt}) = 0,3.
Die Zufallsvariable X gebe die Anzahl defekter Systeme im betrachteten Zeitraum an.
a) Berechnen und skizzieren Sie die Wahrscheinlichkeitsfunktion von X!
b) Berechnen und skizzieren Sie die Verteilungsfunktion von X!
c) Wie groß ist die Wahrscheinlichkeit dafür, dass im betrachteten Zeitraum
c1) höchstens ein System
c2) mehr als ein System ausfällt?
d) Berechnen Sie den Erwartungswert, die Varianz und die Standardabweichung von X!
Aufgabe 5 (Kontinuierliche Zufallsvariable)
04. Nov. 2011
Es werde der Zugriff auf eine Festplatte betrachtet, die sich mit der Frequenz f = 6000 min-1 dreht
(Bild 5.1). Zwischen dem Zeitpunkt des Zugriffswunsches auf einen Datensatz und dem Passieren der
Satzanfangsadresse unter den Schreib-/Leseköpfen vergeht die sog. Rotationslatenzzeit. Diese physikalische Größe hat Zufallscharakter und kann durch eine Zufallsvariable T modelliert werden
-1
Magnetplatte
f = 6000 min
Spur
t = T (Latenzzeit)
Arm mit Schreib-/Leseköpfen
Datensatz
t=0
Bild 5.1 Rotationslatenzzeit T beim Festplattenzugriff
a) Welchen Wertebereich kann die Zufallsvariable T annehmen?
b) Geben Sie die Wahrscheinlichkeitsdichte f(t) für T an und skizzieren Sie deren Verlauf!
c) Berechnen Sie die Verteilungsfunktion F(t) von T und skizzieren Sie deren Verlauf!
d) Berechnen Sie den Erwartungswert, die Varianz und den Variationskoeffizient von T!
© Prof. Dr. W. Schmitt | Leistungsanalyse & -bewertung …| Wahrscheinlichkeitsrechnung
4
Aufgabe 6 (Kontinuierliche Zufallsvariable)
25. Okt. 2011
Die Zufallsvariable X werde durch die folgende Verteilungsfunktion beschrieben:
F(x)
0
2
x − 3 x+ 9
2
F( x) = P( X ≤ x) = 8 2 2
x
5
23
−
+ x−
8 2
2
1
(Skizze)
1
für
x<6
für
6≤ x≤8
für
8 < x ≤ 10
0,5
x
0
sonst
5
6
8
10
a) Berechnen Sie die folgenden Wahrscheinlichkeiten
a1) P(X ≤ 7)
a2) P(X > 9)
a3) P(7 < X ≤ 9).
b) Berechnen und skizzieren Sie die Wahrscheinlichkeitsdichte f(x)!
c) Berechnen Sie Mittelwert, Varianz und Standardabweichung von X!
d) Die oben definierte Dreiecksverteilung soll hinsichtlich der Streuung mit einer Gleichverteilung
verglichen werden, die durch
0
f(x) =
1
b−a
0
für x ≤ a
für a < x < b
mit E( X ) =
a+b
2
und
Var( X ) =
(b − a )
12
für b ≤ x
definiert ist. Die Parameter seien a = 6 und b = 10. Ermitteln Sie durch Vergleich der Variationskoeffizienten, welche der beiden Verteilungen stärker streut!
Aufgabe 7 (Poissonverteilung)
25. Oktober 2011
Ein Callcenter erhalte während der Hauptverkehrsstunde im Mittel 300 Anrufe pro Stunde. Es sei angenommen, dass die Anzahl der Anrufe in einem vorgegebenen Zeitintervall eine poissonverteilte
Zufallsvariable ist. Wie groß ist die Wahrscheinlichkeit, dass in einer Minute mehr als 10 Anrufe eintreffen?
Aufgabe 8 (Exponentialverteilung)
25. Oktober 2011
In einem Callcenter seien die zufälligen Wartezeiten TW exponentiell verteilt. Die mittlere Wartezeit w
eines Kunden betrage 25s.
a) Mit welcher Wahrscheinlichkeit muss ein Kunde höchstens 25s warten?
b) Mit welcher Wahrscheinlichkeit muss ein Kunde, der bereits 30s gewartet hat, noch mehr als 10s
warten?
© Prof. Dr. W. Schmitt | Leistungsanalyse & -bewertung …| Wahrscheinlichkeitsrechnung











