Vektoren

8
Vektoren
Sowohl in Wirtschaft und Technik als auch in der Geometrie
werden Vektoren verwendet, um dynamische Prozesse zu beschreiben. Zum Beispiel stellen viele Grafikprogramme bewegte
Bilder mithilfe von Vektoren dar. Vektoren in der Ebene, also im
zweidimensionalen Raum ℝ2, deren Definition und Darstellung sowie einige Rechenoperationen wurden bereits in Band 1, Abschnitt
9, behandelt. Dieser Abschnitt widmet sich nun unter anderem
auch Berechnungen mit Vektoren im dreidimensionalen Raum ℝ3.
8.1 Wiederholung der Grundbegriffe
()
ax
versteht man die Menge aller gleich
ay
langen, gleich gerichteten und gleich orientierten Pfeile. Ein einzelner
Pfeil wird Repräsentant des Vektors genannt. Repräsentanten mit dem
–⃑.
Ursprung als Anfangspunkt bezeichnet man als Ortsvektoren, zB OA
–⃑ = B – A („Endpunkt minus Anfangspunkt“)
Vektor von A nach B: AB
Unter einem Vektor a⃑ =
AB
OB
A
OA
O
1
a–⃑0 = __
· a⃑
| |
Addition bzw. Subtraktion von Vektoren:
a
b
a ±b
a⃑ ± b⃑ = x ± x = x x
ay
by
ay ± by
Multiplikation mit einer reellen Zahl:
a
s · ax
s · a⃑ = s · x =
ay
s · ay
Mittelpunkt der Strecke AB:
MAB = 1_2 · (A + B)
Schwerpunkt des Dreiecks ABC:
S = 1_3 · (A + B + C)
()()( )
212
B
Betrag (Länge) des Vektors a⃑:
a
2
2
| a⃑ | = x = ––––––
√ ax + ay
ay
x
Einheitsvektor:
|( )|
A B C
y
a⃑
()( )
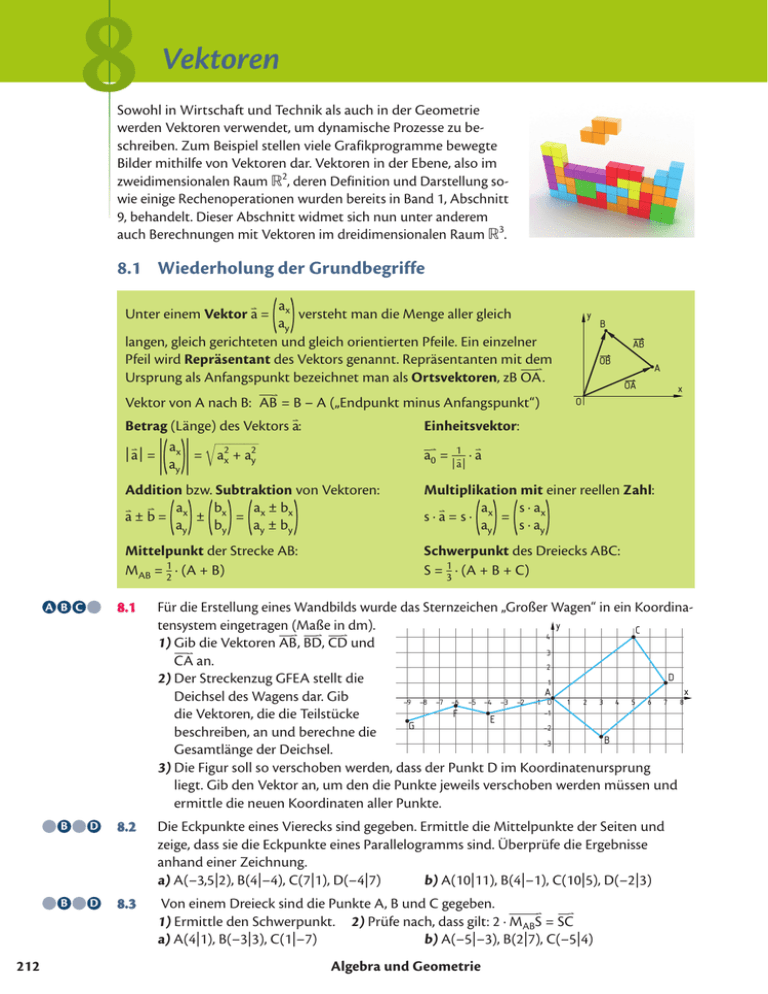
8.1
Für die Erstellung eines Wandbilds wurde das Sternzeichen „Großer Wagen“ in ein Koordinay
tensystem eingetragen (Maße in dm).
C
4
–
–
–
⃑
⃑
⃑
1) Gib die Vektoren AB , BD, CD und
3
–⃑ an.
CA
2
D
2) Der Streckenzug GFEA stellt die
1
x
A
Deichsel des Wagens dar. Gib
-9 -8 -7 -6 -5 -4 -3 -2 -1 O
1
2 3 4 5 6 7 8
-1
F
die Vektoren, die die Teilstücke
E
G
-2
beschreiben, an und berechne die
B
-3
Gesamtlänge der Deichsel.
3) Die Figur soll so verschoben werden, dass der Punkt D im Koordinatenursprung
liegt. Gib den Vektor an, um den die Punkte jeweils verschoben werden müssen und
ermittle die neuen Koordinaten aller Punkte.
B
D
8.2
Die Eckpunkte eines Vierecks sind gegeben. Ermittle die Mittelpunkte der Seiten und
zeige, dass sie die Eckpunkte eines Parallelogramms sind. Überprüfe die Ergebnisse
anhand einer Zeichnung.
a) A(–3,5|2), B(4|–4), C(7|1), D(–4|7)
b) A(10|11), B(4|–1), C(10|5), D(–2|3)
B
D
8.3
Von einem Dreieck sind die Punkte A, B und C gegeben.
–⃑
1) Ermittle den Schwerpunkt. 2) Prüfe nach, dass gilt: 2 · –
MABS⃑ = SC
a) A(4|1), B(–3|3), C(1|–7)
b) A(–5|–3), B(2|7), C(–5|4)
Algebra und Geometrie
Vektoren
8.2 Normalvektoren
8.4
()
2
grafisch dar. Zeichne einen Vektor mit der gleichen Länge ein,
5
der auf a⃑ im rechten Winkel steht, und lies seine Koordinaten ab. Beschreibe den
Zusammenhang zwischen den Koordinaten der beiden Vektoren.
Stelle den Vektor a⃑ =
B C
Zwei Vektoren, die normal aufeinander stehen, werden orthogonal genannt. Die Begriffe
„orthogonal“ bzw. „Orthogonalität“ setzen sich aus den altgriechischen Wörtern für „gerade,
recht, richtig“ (orthos) und „Winkel, Ecke“ (gonia) zusammen.
()
2
wird um 90° in mathematisch positive Richtung,
1
–1
also gegen den Uhrzeigersinn (nach links), gedreht. Man erhält: n–⃑L =
2
2
Wird der Vektor a⃑ =
um 90° in mathematisch negative Richtung,
1
1
also im Uhrzeigersinn (nach rechts), gedreht, so erhält man: n–⃑R =
–2
ZB: Der Vektor a⃑ =
()
()
()
-1
y
2
nL
a
2
1
x
nR
-2
1
Normalvektoren
–ay
a
... der durch Linksdrehung entstandene Normalvektor von a⃑ = x
n–⃑L =
ax
ay
( )
( )
()
()
a
a
n–⃑R = y ... der durch Rechtsdrehung entstandene Normalvektor von a⃑ = x
ay
–ax
8.5
Ist der gegebene Normalvektor durch eine Rechts- oder durch eine Linksdrehung
entstanden? Begründe deine Antwort.
8
–4 –
–7
–5 –
3
1
a) a⃑ = , n–⃑a =
b) b⃑ =
, n⃑b =
c) c⃑ =
, n⃑ =
3
7
–4
–1 c –5
–8
–⃑ an.
Gib die Koordinaten beider Normalvektoren des Vektors AB
() ( )
8.6
() ( )
C D
( ) ()
B
a) A(6|–1), B(11|–13) b) A(3|–1), B(3|4) c) A(–4|–10), B(2|–4) d) A(7|8), B(4|8)
Aufgaben 8.7 – 8.9: Berechne jeweils die fehlenden Koordinaten der weiteren Eckpunkte.
Überprüfe deine Rechnung anhand einer Zeichnung.
8.7
Die Strecke BC mit B(–3|–3) und C(4|–2) ist eine Kathete eines gleichschenkligrechtwinkligen Dreiecks, wobei der rechte Winkel im Eckpunkt C liegt. Gib beide
Lösungen an.
A B
D
8.8
Die Strecke AB mit A(3|4) und B(7|6) ist die Seitenkante eines Quadrats. Gib beide
Lösungen an.
A B
D
8.9
Die Strecke AC mit A(–6|5) und C(3|–7) ist die Diagonale e einer Raute.
a) Die Diagonale f ist doppelt so lang wie die Diagonale e.
b) Die Länge der Diagonale f ist ein Drittel der Länge der Diagonale e.
A B
D
8.10 In welchem besonderen Dreieck ist der Normalvektor einer Seite jeweils ein Vektor in
Richtung einer Schwerlinie? Begründe deine Antwort.
Algebra und Geometrie
C D
213
Vektoren
8.3 Skalarprodukt zweier Vektoren
D
8.11 Zwei Leiterwagerln mit der gleichen Masse
werden entlang einer geraden Strecke
gezogen. Bei welchem Bewegungsablauf
muss man sich mehr anstrengen?
Begründe deine Entscheidung.
Aus dem naturwissenschaftlichen Unterricht ist bekannt, dass die
Arbeit W gleich dem Produkt aus den Beträgen der vektoriellen
Größen Kraft in Wegrichtung F–⃑s und Weg ⃑s ist: W = | F–⃑s | · | ⃑s |
Dabei ist F–⃑ die Normalprojektion des Vektors F⃑ auf die Richtung ⃑s.
F
s
s
Es gilt:
Fs
–
| F⃑s |
AK
⃑|
⃑ s | · cos(φ)
= ___
⇒ | F–⃑|
cos(φ) = ___
s = | F · cos(φ) ⇒ W = | F | · | ⃑
HYP
⃑
|F|
F⃑ und ⃑s sind gerichtete Größen, die Arbeit W ist aber keine gerichtete Größe, sondern ein
so genannter Skalar. Sie kann als das Produkt der Beträge der Vektoren F⃑ und ⃑s und dem
Cosinus des von den beiden Vektoren eingeschlossenen Winkels φ berechnet werden. Diese
Multiplikation bezeichnet man als skalare Multiplikation der Vektoren F⃑ und ⃑s , das Ergebnis
heißt Skalarprodukt.
Man schreibt: W = F⃑ · ⃑s
Allgemein gilt für das Skalarprodukt von zwei Vektoren a⃑ und b⃑:
a⃑ · b⃑ = | a⃑ | · | b⃑ | · cos(φ) = | a⃑ | · | b–⃑′ |
| b–⃑′ | ... Länge der Normalprojektion von b⃑ auf a⃑
b
bI
a
bI
Geometrisch kann das Skalarprodukt als Größe des Flächeninhalts des
Rechtecks mit den Seitenlängen | a⃑ | und | b–⃑′ | interpretiert werden.
a
Projiziert man umgekehrt den Vektor a⃑ auf b⃑, so erhält man | a–⃑′ | = | a⃑ | · cos(φ) und es gilt:
a⃑ · b⃑ = b⃑ · a⃑
Ist b⃑ = a⃑, so erhält man:
a⃑ · a⃑ = | a⃑ |2
Stehen die beiden Vektoren aufeinander normal, dann ist die Länge der Projektion | b–⃑′ | = 0.
Damit ist der Flächeninhalt und daher auch das Skalarprodukt null.
Ist das Skalarprodukt zweier Vektoren null, so bezeichnet man sie als orthogonal. Sind in
diesem Fall beide Vektoren vom Nullvektor o⃑ verschieden, so schließen sie einen rechten Winkel
ein. Der Nullvektor ist zu jedem Vektor orthogonal. Sind a⃑ , b⃑ ≠ o⃑ , so gilt:
a⃑ · b⃑ = 0 ⇔ a⃑ ⊥ b⃑
Weiters gilt für das Skalarprodukt:
a⃑ · (b⃑ + c⃑) = a⃑ · b⃑ + a⃑ · c⃑ und s · (a⃑ · b⃑) = (s · a⃑ ) · b⃑ = a⃑ · (s · b⃑)
Skalarprodukt zweier Vektoren a⃑ , b⃑
a⃑ · b⃑ = | a⃑ | · | b⃑ | · cos(φ) = | a⃑ | · | b–⃑′ |
b
Stehen Vektoren aufeinander normal, ist ihr Skalarprodukt null.
b‘
214
Algebra und Geometrie
a
Vektoren
Berechnung des Skalarprodukts in Koordinatenschreibweise
Meist wird das Skalarprodukt nicht mithilfe der Definition berechnet, sondern anhand der
Koordinaten der Vektoren.
y
Man kann eine Formel zur Berechnung des Skalarprodukts mithilfe
e–⃑1 =
1
–
–
der Basisvektoren e⃑1 und e⃑2 entwickeln. Das sind jene Vektoren, die
in Richtung der Koordinatenachsen verlaufen und 1 Einheit lang sind. e2
–⃑ =
x e
2
O
1
e1
Jeder Vektor kann mithilfe der Basisvektoren dargestellt werden.
a⃑ =
()
()
1
0
0
1
() () ()
5
1
0
=5·
+8·
8
0
1
Allgemein bezeichnet man jeden Ausdruck der Form r · ⃑a + s · b⃑ , mit r, s∊ℝ als
Linearkombination.
Für a⃑ =
()
()
ax
b
= ax · e–⃑1 + ay · e–⃑2 und b⃑ = x = bx · e–⃑1 + by · e–⃑2 gilt nun:
ay
by
{
{
{
a⃑ · b⃑ = (ax · e–⃑1 + ay · e–⃑2 ) · (bx · e–⃑1 + by · e–⃑2 ) =
• Produkt der Linearkombinationen
–
–
–
–
–
–
= ax · bx · e⃑1 · e⃑1 + ay · bx · e⃑1 · e⃑2 + ax · by · e⃑1 · e⃑2 + ay · by · e–⃑2 · e–⃑2 =
= ax · bx · e–⃑1 2 + (ay · bx + ax · by) · e–⃑1 · e–⃑2 + ay · by · e–⃑2 2
• e–⃑1 und e–⃑2 stehen normal
aufeinander: e–⃑1 · e–⃑2 = 0
=1
=0
=1
• e–⃑1 · e–⃑1 = |e–⃑1 |2 = 1
a⃑ · b⃑ = ax · bx + ay · by
e–⃑2 · e–⃑2 = |e–⃑2 |2 = 1
()
()
2
3
und b⃑ = :
2
0
Die Vektoren a⃑ und b⃑ schließen den Winkel φ = 45° ein.
1. Möglichkeit:
2. Möglichkeit:
a⃑ · b⃑ = | a⃑ | · | b⃑ | · cos(φ)
a⃑ · b⃑ = ax · bx + ay · by
1
= √––
8 · 3 · ___ = 2 · 3 = 6
=2·3+2·0=6
Berechnung des Skalarprodukts der Vektoren a⃑ =
y
2
a
1
= 45°
O
1
b
2
x
3
––
√2
Berechnung des Skalarprodukts in Koordinatenschreibweise
a
b
a⃑ · b⃑ = x · x = ax · bx + ay · by
ay by
()( )
8.12 Beschreibe, wie man nachprüfen kann, ob die gegebenen Vektoren a⃑ und b⃑ normal
aufeinander stehen.
12,5 ⃑
7
, b=
a⃑ =
35
–2,5
C
( ) ( )
Lösung:
Zwei Vektoren a⃑ , b⃑ ≠ o⃑ stehen normal aufeinander, wenn ihr Skalarprodukt null ist.
( )( )
12,5
7
·
= 12,5 · 7 + 35 · (–2,5) = 87,5 – 87,5 = 0
35
–2,5
Die beiden Vektoren a⃑ und b⃑ stehen normal aufeinander.
Algebra und Geometrie
215
Vektoren
Da das Skalarprodukt auf zwei Arten berechnet werden kann, ist es möglich, eine Formel für den
Winkel φ zwischen zwei Vektoren anzugeben.
y
a⃑ · b⃑
4
_____
⃑
⃑
|
|
|
|
a⃑ · b = a⃑ · b · cos(φ) ⇒ cos(φ) =
| a⃑ | · | b⃑ |
Der Scheitel des Winkels φ liegt im gemeinsamen Anfangspunkt
der Repräsentanten der Vektoren.
Anhand des Vorzeichens des Skalarprodukts kann bereits
entschieden werden, ob der Winkel spitz oder stumpf ist.
• a⃑ · b⃑ > 0
• a⃑ · b⃑ < 0
⇒ 0° < φ < 90°
⇒ 90° < φ < 180°
3
b
a
2
a
1
x
O
1
2
3
4
5
Für den Winkel 𝛗 zwischen zwei Vektoren a⃑ und b⃑ gilt:
a⃑ · b⃑
cos(φ) = _____
| a⃑ | · | b⃑ |
B
D
8.13 1) Berechne den Winkel φ = ∢PQR mithilfe von u⃑ und v⃑.
2) Erkläre, welchen Winkel φ′ man erhält, wenn man den
–⃑ ansetzt.
Vektor u⃑ irrtümlich mit u⃑ = PQ
O
( ) ()
R
u
v
Q
x
1
2
3
4
5
( ) ()
–⃑ = 2 – 1 = 1
u⃑ = QP
3–1
2
–⃑ = 4 – 1 = 3
v⃑ = QR
2–1
1
()()
·
P
2
1
Lösung:
1) P(2|3), Q(1|1), R(4|2)
1
y
3
3
2 1
5
u⃑ · v⃑
= ______ = ___
= 0,707... ⇒ φ = arccos(0,707...) = 45°
cos(φ) = _____
| | | |
u⃑ · v⃑
–– –––
√ 5 · √ 10
–––
√ 50
–⃑, so muss der Anfangspunkt von PQ
–⃑ zuerst in Q verschoben werden.
2) Wählt man u⃑ = PQ
Man erhält einen stumpfen Winkel: φ′ = 180° – φ = 135°
Flächeninhalt von Parallelogrammen und von Dreiecken
Zwei Vektoren spannen ein Parallelogramm auf. Dessen Flächeninhalt
b
kann mithilfe des Skalarprodukts berechnet werden.
ha
–
2
2
2
AP = a · ha = | a⃑ | · ha mit ha = | b⃑ | – | b⃑′ |
a
bI
| b⃑ |2 – | b–⃑′ |2
AP = | a⃑ | · √––––––––––
| a⃑ |2 · | b⃑ |2 – | a⃑ |2 · | b–⃑′ |2 = √––––––––––––––––
a⃑ 2 · b⃑ 2 – (| a⃑ | · | b–⃑′ |)2
AP = √––––––––––––––––––
• | a⃑ |2 = a⃑2; | a⃑ | · | b–⃑′ | = a⃑ · b⃑
a⃑ 2 · b⃑ 2 – (a⃑ · b⃑)2
AP = √––––––––––––
AP = |axby – aybx|
• Mehrmaliges Ausführen des Skalarprodukts
und Umformen.
Der Flächeninhalt AD eines Dreiecks kann mithilfe von AD = _12 · AP berechnet werden.
Flächeninhalt eines Parallelogramms: AP = √––––––––––––
a⃑ 2 · b⃑ 2 – (a⃑ · b⃑)2 = |axby – aybx|
Flächeninhalt eines Dreiecks:
216
a⃑ 2 · b⃑ 2 – (a⃑ · b⃑)2 = 1_2 · |axby – aybx|
AD = _12 · AP = 1_2 · √––––––––––––
Algebra und Geometrie
Vektoren
8.14 Von einem Parallelogramm sind die Punkte A(1|–2), B(5|1) und C(–1|2) bekannt.
1) Fertige eine Zeichnung an und ermittle die Koordinaten des Eckpunkts D auf zwei Arten.
2) Berechne den Flächeninhalt des Parallelogramms.
Lösung:
1)
C
y
2
b
x
-4
-3
-2
-1
0
1
2
-2
D = A + b⃑ =
5
a
-1
D
4
3
( ) ()
( )()
( ) () ( )
–⃑ =
a⃑ = AB
B
1
-5
A B
A
()()()
5–1
4
=
3
1 – (–2)
–⃑ = (–1) – 5 = –6
b⃑ = BC
1
2–1
–6
–5
–1
4
–5
1
+
=
oder D = C – a⃑ =
–
=
⇒ D(–5|–1)
1
–1
2
3
–1
–2
2) AP = |ax · by – ay · bx| = |4 · 1 – 3 · (–6)| = 22 E2
Technologieeinsatz: Skalares Produkt
TE
TI-Nspire
Vektoren werden mithilfe von eckigen Klammern [ ]
oder über „mathematische Vorlagen“ eingegeben.
Bei Spaltenvektoren werden Strichpunkte zur Eingabe
verwendet (zB [2;3]), bei Zeilenvektoren verwendet
man Beistriche (zB [4,5]).
Das Skalarprodukt wird mit dem Befehl dotP( berechnet, der direkt eingegeben oder über das
Menü 7: Matrix und Vektor, C: Vektor, 3: Skalarprodukt ausgewählt werden kann.
8.15 Setze die Worte „positiv“ oder „negativ“ ein und begründe deine Antwort:
„Schließen zwei Vektoren einen spitzen Winkel ein, so ist ihr Skalarprodukt ...,
schließen sie einen stumpfen Winkel ein, so ist es ... .“
8.16 Der Vektor b⃑ aus nebenstehender Skizze kann um einen
beliebigen Winkel gedreht werden, während a⃑ fest
bleibt. Beschreibe, wie sich dabei das Skalarprodukt der
beiden Vektoren ändert. Welchen Wert nimmt es
höchstens an, welchen mindestens?
–⃑
8.17 Schreibe den Vektor AB
C D
y
C
2
1
b
x
-1
O
1
2
a
3
B
1) als Summe aus einem senkrechten und einem waagrechten Vektor an.
2) als Linearkombination der Einheitsvektoren e–⃑1 und e–⃑2 an.
a) A(3|11), B(−8|9)
b) A(−34|0), B(25|37)
c) A(1,5|2), B(0|4,5)
8.18 Berechne das Skalarprodukt der beiden Vektoren.
6
–9 ⃑ 5
2
a) a⃑ = , b⃑ =
b) a⃑ =
,b=
8
–4
3
–1
() ( )
( ) ()
B
c) a⃑ =
() ( )
11 ⃑ –4
,b=
0
2
8.19 Überprüfe die Aussagen anhand der Vektoren a⃑, b⃑ und c⃑ .
–35
23 ⃑ –48
,b=
, c⃑ =
a⃑ =
55
–28
–17
1) a⃑ · b⃑ = b⃑ · a⃑
2) a⃑ · (b⃑ + c⃑) = (a⃑ + b⃑) · c⃑
D
( ) ( ) ( )
Algebra und Geometrie
217
Vektoren
D
() ( )
()
B
()
8.23 Berechne die Größen der Innenwinkel des Dreiecks mit den angegebenen Eckpunkten.
a) G(–4|2), H(–6|–4), I(4|–6)
b) K(0|–3), L(3|5), M(–9|1)
B
D
8.24 Der Winkel φ zwischen den beiden Vektoren a⃑ und b⃑ ist gegeben. Berechne die fehlende
Koordinate. Wie viele Lösungen sind möglich? Begründe deine Antwort mithilfe einer
Zeichnung.
a
–3 ⃑ –9
5
a) a⃑ =
,b=
, φ = 60°
b) a⃑ = x , b⃑ =
, φ = 30,51°
by
–4
3
12
( ) ( )
D
B
() ( )
ax
3
und b⃑ =
stehen normal aufeinander. Ermittle ax.
1
2
–⃑.
8.22 Berechne den Winkel zwischen den Vektoren a⃑ = –
BA⃑ und b⃑ = BC
a) A(–2|–9), B(–7|3), C(–4|7)
b) A(5|–3), B(9|8), C(17|3)
8.21 Die Vektoren a⃑ =
B
B
8.20 Überprüfe auf zwei Arten, ob die Vektoren normal aufeinander stehen.
35 ⃑ –39
2 ⃑
3
a) a⃑ =
,b=
b) a⃑ =
,b=
65
–15
–8
0,75
D
B
A B C D
() ()
8.25 Welchen Winkel schließen zwei Vektoren a⃑ und b⃑ ein, wenn folgende Aussage gilt?
Begründe deine Antwort mithilfe einer Skizze.
1) a⃑ · b⃑ = | a⃑ | · | b⃑ |
2) a⃑ · b⃑ = –| a⃑ | · | b⃑ |
3) a⃑ · b⃑ = 1_2 · | a⃑ | · | b⃑ |
8.26 a) Überprüfe, ob die Punkte A(1|2), B(5|5), C(2|9) und D(–2|6) ein Quadrat bilden.
b) Überprüfe, ob die Punkte A(–1|–2), B(1|–3) und C(4|2) ein rechtwinkliges Dreieck bilden.
8.27 Ermittle die fehlenden Koordinaten sowie den Flächeninhalt des angegebenen
Parallelogramms mithilfe der Vektorrechnung.
a) A(10|5), B(2|3), C(xC|yC), D(13|5)
b) A(xA|yA), B(–5|–7), C(–2|5), D(–11|9)
8.28 Ein viereckiges Maisfeld ist durch die Punkte A, B, C
12 y
11
und D begrenzt. Im Punkt S befindet sich der GeräteC
D
10
schuppen des Bauern (siehe Grafik, Angaben in 100 m).
9
8
1) Gib jeweils die Vektoren der Begrenzungslinien AB,
7
BC, CD und DA an und berechne den Flächeninhalt
6
5
des Maisfelds.
4
2) Zeige, dass der Schuppen S auf der Strecke BC liegt.
S
3
3) Es soll ein Verbindungsweg zwischen dem Schuppen
2
A
1
und dem Mittelpunkt der Strecke AD errichtet
B
x
0
1 2 3 4 5 6 7 8 9 10 11 12
werden. Ermittle die Länge des Wegs und den
Winkel, den er mit der Strecke AD einschließt.
4) Um die Ernte zu schützen, stellt der Bauer eine Vogelscheuche V auf. Deren Standort
teilt die Strecke AC im Verhältnis 3 : 1. Ermittle die Koordinaten von V und zeichne die
Position der Vogelscheuche in das Koordinatensystem ein.
5) Eine Krähe ist auf der Suche nach einem Nistplatz. Sie fliegt vom Punkt D weg. Ihre
Nistplatzsuche wird durch folgende Vektoren beschrieben:
2
1 ⃑ 2,5
,b=
, c⃑ =
a⃑ =
–3
7
–6
Zeichne diese Vektoren in das Koordinatensystem ein und gib den Endpunkt an.
( ) ( ) ()
218
Algebra und Geometrie
Vektoren
8.29 Es soll der Flächeninhalt eines Dreiecks mit den Punkten A(–6|–7), B(9|1) und C(–3|6)
berechnet werden (Einheiten in cm).
1) Kenan rechnet diese Aufgabe mithilfe der trigonometrischen Flächenformel:
y
C
6
–⃑ = 15 , c = | c⃑ | = 17 cm
c⃑ = AB
5
8
4
()
( )
C D
a
–⃑ = –12 , a = | a⃑ | = 13 cm
a⃑ = BC
5
( )( )
cos(β) = _____ = _______ = – ___ = –0,633...
a⃑ · c⃑
| a⃑ | · | c⃑ |
A
–12 15
·
5
8
13 · 17
140
221
b
3
2
1
-7 -6 -5 -4 -3 -2 -1 0
-1
-2
-3
-4
-5
-6
-7
A
B
x
1
2
3
4
5
6
7
8
9
c
β = arccos(–0,633...) ≈ 129,31°
a · c · sin(β)
13 · 17 · sin(129,31°)
= ____________
= 85,5 cm2
A = _______
2
2
Überprüfe die Rechenschritte und gib an, welchen Fehler Kenan gemacht hat.
Erkläre, warum die berechnete Maßzahl des Flächeninhalts dennoch richtig ist.
2) Gib zwei weitere Methoden zur Berechnung des Flächeninhalts an und dokumentiere
jeweils die Vorgehensweise.
8.30 Berechne den Flächeninhalt des gegebenen Dreiecks auf drei verschiedene Arten.
a) A(7|11), B(–9|1), C(2|–7)
b) A(–4|–3), B(5|0), C(–2|–8)
A B
8.31 Ein gleichschenkliges Dreieck ABC, das in mathematisch positiver Richtung beschriftet ist,
hat die Basis AB mit A(–2|–1), B(4|7) sowie die Höhe h = 10 E. Ermittle den fehlenden
–⃑ mit AC
–⃑ einschließt sowie den Flächeninhalt
Eckpunkt C, berechne den Winkel φ, den AB
des Dreiecks.
B
8.32 Ein Viereck ist durch die Punkte A(–5|–6), B(7|3), C(0|4) und D(–4|1) bestimmt.
1) Zeige, dass es sich dabei um ein gleichschenkliges Trapez handelt.
2) Berechne den Umfang, die Innenwinkel sowie den Flächeninhalt des Trapezes.
B
8.33 Bei einem Ruderbewerb müssen auf einem See zwei Bojen an
den Positionen B1(150|140) und B2(500|250) passiert werden.
Danach soll zum Startpunkt zurückgekehrt werden. Ein
Ruderteam startet im Punkt A(120|10) (Angaben in Meter).
1) Berechne, in welchem Winkel zur Horizontalen das
Team die erste Boje B1 mindestens ansteuern sollte.
–⃑
⃑
2) Ermittle den Winkel zwischen B–
1A und B1B2 .
3) Berechne, welche Wasserfläche durch den Parcours AB1B2 eingeschlossen wird.
D
A B
8.34 Überprüfe den folgenden Satz anhand des gegebenen Dreiecks ABC:
„Die Verbindungsstrecken zwischen dem Schwerpunkt und den Eckpunkten eines
Dreiecks teilen das Dreieck in drei flächengleiche Dreiecke.“
a) A(6|5), B(–2|5), C(–1|–2)
b) A(10|0), B(4|–4), C(–5|–2)
D
8.35 Zeige, dass die folgenden Eigenschaften des Skalarprodukts gelten. Begründe dies jeweils,
ohne die Koordinatenschreibweise zu verwenden.
1) a⃑ · b⃑ = b⃑ · a⃑
2) a⃑ · a⃑ = | a⃑ |2
3) s · (a⃑ · b⃑) = (s · a⃑) · b⃑
D
8.36 Beweise den folgenden Satz mithilfe des Skalarprodukts.
a) Satz von Pythagoras
b) Satz von Thales
c) Cosinussatz
Algebra und Geometrie
A B
D
219
Vektoren
8.4 Anwendungen der Vektorrechnung im ℝ2
Wirken mehrere Kräfte in einem Punkt, so kann die resultierende Kraft durch
F3
F2
Addition der Einzelkräfte berechnet werden. Grafisch erfolgt dies durch
die vektorielle Addition. Dadurch entsteht ein Kräfteeck. Die resultierende
FR
Kraft verbindet den Anfangspunkt mit dem Endpunkt. Ist das Kräfteeck
geschlossen, so ist die resultierende Kraft der Nullvektor und das System im
F1
Gleichgewicht. Bei drei Kräften spricht man dann von einem Kräftedreieck.
Die resultierende Kraft von zwei Kräften kann auch mithilfe eines Kräfteparallelogramms
ermittelt werden (siehe Band 1, Abschnitt 9.3.2). Soll eine Kraft in zwei Kräfte zerlegt werden, deren
Wirkungslinien bekannt sind, so kann das Kräfteparallelogramm ebenfalls verwendet werden.
Auch andere gerichtete Größen wie der Weg s oder die Geschwindigkeit v können mithilfe von
Vektoren beschrieben werden.
Lösung:
1)
1,5 m
0,5 m
8.37 Eine Lampe mit dem Gewicht FG = |F–G⃑| = 45 N soll mithilfe von
zwei Stäben s1 und s2 an einer senkrechten Wand montiert
werden (Abmessungen siehe Abbildung).
1) Skizziere das Kräftedreieck der Kräfte, die im Aufhängepunkt A
der Lampe wirken, und gib deren Richtungen an.
2) Berechne die Beträge der Kräfte, die in den Stäben wirken.
1,0 m
A B C
y
s1
A
x
FG
s2
Die Richtung der Kraft F–⃑1 ergibt sich aus der Richtung von
A
–1,5
s–⃑1 =
.
FG
0,5
F2
1,5
Analoges gilt für die Richtung der Kraft F–⃑2: s–⃑2 =
1
0
–
Die Gewichtskraft weist senkrecht nach unten: FG⃑ =
–45
2) Die Summe der in A angreifenden Kräfte muss der Nullvektor sein:
F–G⃑ + F–⃑1 + F–⃑2 = o⃑ bzw. F–⃑1 + F–⃑2 = –F–G⃑
Kräftegleichung als Linearkombination
–1,5
1,5
0
r·
+t·
=
der Richtungsvektoren der Stäbe
0,5
1
45
Zerlegen der Komponenten in
I: –1,5r + 1,5t = 0 ⇒ t = r
ein lineares Gleichungssytem und
II: 0,5r + t = 45
Ermitteln der Faktoren r und t.
I in II: 1,5 · r = 45 ⇒ r = 30, t = 30
–45
45
F–⃑2 = t · s–⃑2 = t ·
F–⃑1 = r · s–⃑1 =
15
30
|F–⃑1| = 47,343... N ≈ 47 N
|F–⃑2| = 54,083... N ≈ 54 N
F1
( )
( )
( )
( ) ( )()
•
•
( )
A B
()
8.38 Zwei Kräfte F–⃑1 und F–⃑2 greifen im selben Punkt an. Ermittle die resultierende Kraft F–R⃑ und
den Winkel zwischen F–⃑1 und F–⃑2 (Angaben in N).
10 –⃑
130 –⃑ 240
4
1,3 –⃑ 2,3
a) F–⃑1 =
, F2 =
b) F–⃑1 =
, F2 =
c) F–⃑1 =
,F =
5
17
–0,7
3,1
570 2
90
–
–
–
8.39 Die Kräfte F⃑, F⃑ und F⃑ bilden ein Kräftedreieck. Ermittle die fehlende Kraft grafisch und
() ()
A B
1
2
( ) ( )
( ) ( )
3
rechnerisch so, dass das Kräftesystem im Gleichgewicht ist (Angaben in kN).
20 –⃑ –10 –⃑
2,3 –⃑ –1,8 –⃑
a) F–⃑1 =
,F =
,F =?
b) F–⃑2 =
,F =
,F =?
30 2
15 3
–4,2 3 –3,6 1
() ( )
220
( ) ( )
Algebra und Geometrie
Vektoren
8.40 An der Hausecke einer Buschenschank ist ein Symbol in
Form eines gusseisernen Kelchs mit einer Masse von m = 9 kg
montiert (siehe Abbildungen). Die waagrechte Strebe s1 ist
120 cm lang, der Montagepunkt der schrägen Strebe s2 an
der Hausecke liegt 30 cm senkrecht unter dem der Strebe s1.
1) Skizziere das Kräftedreieck der Kräfte, die im Aufhängepunkt A des Kelchs wirken und gib deren Richtungen an.
2) Berechne die Beträge der Kräfte und die Winkel, die sie
miteinander einschließen.
A B
s1
A
s2
8.41 Bei Damenbewerben im Sportbogenschießen beträgt die größte Zielentfernung 70 m.
Für diese Weite muss eine Zugkraft erreicht werden, die der Gewichtskraft eines Körpers
mit einer Masse von 45 lb entspricht und in horizontale Richtung wirkt. Die Länge des
Bogens wird mit AtA (engl.: „axle to axle“ – Achse zu Achse) bezeichnet und beträgt 70″.
Vor dem Schuss spannt die Sportlerin die Sehne des Bogens so, dass der Pfeil auf der
Auflage in der Mitte des Bogens liegt und sich der Schaft des Pfeils in der Mitte der
gespannten Sehne befindet. Der Pfeil schließt mit der gespannten Sehne auf beiden
Seiten jeweils einen Winkel α = 38,5° ein.
1) Fertige eine Skizze der wirkenden Kräfte an, die den Sachzusammenhang beschreibt.
2) Ermittle die Richtungen und die Beträge der Kräfte, die in der Sehne wirken.
Hinweis: 1 lb (pound) ≈ 0,45 kg, 1″ (Zoll, inch) = 2,54 cm
A B
y
A B C
8.42 Vor dem Paradise Beach auf einer Urlaubsinsel befindet
A
180
sich ein Leuchtturm L. Ein Motorboot B, mit dem Touristen 160
140
zu verschiedenen Stränden der Insel gebracht werden,
L
N
120
km
__
steuert mit einer Eigengeschwindigkeit von vB = 36 h erst
100
den Leuchtturm und anschließend die Anlegestelle A am
80
60
Paradise Beach an (siehe Abbildung, Angaben in m).
40
1) Gib an, um welchen Winkel α das Boot am Leuchtturm
20
x
gewendet werden muss, um zur Anlegestelle zu gelangen.
B
0
20 40 60 80 100 120 140 160 180
2) Aus südlicher Richtung herrscht eine Meeresströmung
__ . Gib an, in welche Richtung der Bootsführer den Kurs
mit der Geschwindigkeit vS = 2 m
s
ändern muss, um vom Punkt B zum Leuchtturm L zu gelangen. Berechne den Betrag
der Geschwindigkeit, mit dem sich das Motorboot nun bewegt.
3) Die Eigengeschwindigkeit des Boots muss für den Weg vom Leuchtturm zur
__ verringert werden. Berechne die Mindestfahrtdauer von der
Anlegestelle um 30 km
h
momentanen Position des Boots B zur Anlegestelle A auf ruhiger See.
8.43 Ein Schlitten wird an einem Seil mit einer konstanten Kraft F entlang einer Strecke s
gezogen. Das Seil schließt mit dem waagrechten Untergrund einen Winkel φ ein.
1) Gib den Richtungsvektor der Kraft an und berechne den Betrag der beim Ziehen
verrichteten Arbeit W.
a) s = 1,8 km; F = | F⃑ | = 45 N; φ = 37°
b) s = 2,3 km; F = | F⃑ | = 55 N; φ = 32°
2) Argumentiere, wie sich die Arbeit verändert, wenn der Winkel φ immer kleiner wird.
3) Erkläre, warum bei einem Winkel von φ = 90° keine Arbeit verrichtet wird.
8.44 Ein Körper wird auf einer Strecke s mit der Steigung k mit einer Kraft F⃑ in Richtung r⃑
gezogen. Berechne die dabei verrichtete Arbeit (F = | F⃑ |).
40
5
a) s = 650 m; k = 10 %; F = 65 N; r⃑ =
b) s = 80 m; k = 5 %; F = 2 870 N; r⃑ =
9
12
()
Algebra und Geometrie
A B
D
A B
()
221
Vektoren
8.5 Vektoren im Raum
A B
8.45 In der linken unteren Ecke eines Zimmers, das 4 m lang, 3 m
breit und 2,5 m hoch ist, sitzen eine Spinne und eine Fliege.
Beide bewegen sich gleichzeitig auf kürzestem Weg zur
rechten oberen Ecke auf der gegenüberliegenden Wand, wobei
die Spinne nur entlang der Raumkanten krabbeln kann.
1) Skizziere jeweils einen möglichen Weg für die Fliege und die Spinne.
2) Berechne diese Weglängen.
Vektoren im Raum werden mithilfe von drei Koordinaten
beschrieben und in einem dreidimensionalen Koordinatensystem veranschaulicht.
Sie werden als dreidimensionale Vektoren bezeichnet:
a⃑ =
()
ax
ay
az
bzw. a⃑ = (ax, ay , az)
ZB: a⃑ =
()
5
3
4
z
4
3
bzw. (5, 3, 4)
() () ()
1
0
0
, e–⃑2 =
0
1
0
, e–⃑3 =
1
e3
e1
Die Basisvektoren e–⃑1 , e–⃑2 und e–⃑3 sind paarweise orthogonal.
e–⃑1 =
A
2
4
0
0
1
x
Bei dreidimensionalen Koordinatensystemen
unterscheidet man zwei Fälle:
• Rechtssystem (Rechtskoordinatensystem,
rechtshändiges Koordinatensystem)
Es gilt die „Rechte-Hand-Regel“.
• Linkssystem (Linkskoordinatensystem,
linkshändiges Koordinatensystem)
6
3
2
a
y
e2 4
1
1
2
3
4
5
5
5
3
Linkssystem
Rechtssystem
Alle Formeln, die in Band 1 und Band 2 für zweidimensionale Vektoren angegeben wurden,
gelten sinngemäß auch für dreidimensionale Vektoren. Einige dieser Formeln und Rechenregeln
sind hier angeführt. Der Betrag eines dreidimensionalen Vektors entspricht der Länge der
Raumdiagonalen eines Quaders mit den Seitenlängen ax, ay und az.
–⃑ = B – A =
Vektor von A nach B: AB
() ()
bx
by
bz
–
ax
ay
az
|( )|
ax
ay
az
= √–––––––––
a2x + a2y + a2z
()
0
0
0
1
Einheitsvektor: a–⃑0 = __
· a⃑
| |
Nullvektor: o⃑ =
Addition und Subtraktion:
Multiplikation mit einem Skalar:
a⃑
a⃑ ± b⃑ =
() () ( )
ax
ay
az
±
bx
by
bz
=
ax ± bx
ay ± by
az ± bz
s · a⃑ = s ·
Skalare Multiplikation: a⃑ · b⃑ = | a⃑ | · | b⃑ | · cos(φ) =
222
Betrag: | a⃑ | =
()()
ax
ay
az
·
bx
by
bz
Algebra und Geometrie
() ( )
ax
ay
az
=
s · ax
s · ay
s · az
mit s∊ℝ
= ax · bx + ay · by + az · bz
Vektoren
Norden
8.46 Auf einer Wanderkarte ist die Talstation T und die Bergstation B
B
einer Seilbahn eingezeichnet. Die Bergstation liegt 927 m höher als
die Talstation. B ist 2 365 m in einem Winkel α = 31° in östlicher
2 365 m
Richtung von T entfernt.
1) Fertige eine räumliche Skizze an. Lege dazu die Talstation in den
Osten
T
Koordinatenursprung und die y-Achse in Richtung Norden.
2) Gib den Vektor b⃑ von der Talstation zur Bergstation an und berechne dessen Länge.
Lösung:
1) z
__
Norden
y
B
2) TF = 2 365 m
bx = 2 365 m · sin(α) = 1 218,0... ≈ 1 218 m
by = 2 365 m · cos(α) = 2 027,2... ≈ 2 027 m
bz = 927 m
bz
b
F
b⃑ =
by
T
Osten
x
bx
( )
1 218
2 027
927
2
2
2
| b⃑ | = ––––––––––
√ bx + by + bz =
1 218,0...2 + 2 027,2...2 + 9272 = 2 540,1...
= √–––––––––––––––––––––––
| b⃑ | ≈ 2 540 m
8.47 Auf einem Balkon soll ein Sonnensegel montiert
werden. Für die Planung wurde eine Skizze mit
folgenden Koordinaten erstellt (Maße in Meter):
P(0|0|3); Q(2,5|0|2); R(0|2,8|2,5)
1) Ermittle den Winkel φ = ∢QPR des Sonnensegels.
2) Die von P nach Q führende Strebe soll um 1,2 m
bis zum Punkt S verlängert werden. Ermittle
dessen Koordinaten.
Lösung:
()
–⃑ =
1) a⃑ = PQ
2,5
0
–1
–⃑ =
; b⃑ = PR
⃑
| a⃑ | · | b |
A B
A B
z
P
R
Q
1
S
y
1
0
1
x
( )
0
2,8
–0,5
a⃑ · b
= ___________________
cos(φ) = _____
= 0,065...
2
2
2
⃑
2,5 · 0 + 0 · 2,8 + 1 · 0,5
2,5 + 0 + 1 · √––––––––––––
0 + 2,8 + 0,5
√––––––––––
φ = arccos(0,065...) = 86,2...° ≈ 86°
Der Winkel φ beträgt rund 86°.
–⃑ = OQ
–⃑ + 1,2 · a–⃑
2) OS
0
()( ) ( )
() ( ) ( )
a⃑
1
= ____
·
a–⃑0 = __
| |
7,25
√––––
a⃑
–⃑ ≈
OS
–⃑
a–⃑0 ... Einheitsvektor von PQ
2,5
0
2
+ 1,2 ·
2,5
0
–1
=
0,93
0
–0,37
0,928...
0
–0,371...
≈
≈
0,93
0
–0,37
3,61
0
1,55
Der Punkt S hat die Koordinaten S(3,61|0|1,55).
Algebra und Geometrie
223
Vektoren
D
8.48 Welche Aussagen sind wahr, welche falsch?
Begründe deine Antworten.
–⃑ = CD
–⃑
–⃑ = AC
–⃑
–⃑
–⃑ = GH
1) AE
3) HB
5) FE
–
–
–
–
–
–⃑
2) EH⃑ = DA⃑
4) AC⃑ = EG⃑
6) BC⃑ = FG
H
G
E
F
D
C
A
B
8.49 Der Eckpunkt A eines Würfels mit der Kantenlänge s = 12 cm liegt im Ursprung eines
kartesischen Koordinatensystems. Alle Koordinaten haben nicht negative Werte.
Ermittle die Koordinaten der fehlenden Eckpunkte, der Mittelpunkte der Seitenflächen
und des Mittelpunkts des Würfels.
–⃑ an und ermittle seine Länge.
8.50 1) Gib den Vektor AB
B
B
2) Vervielfache den Vektor um den Faktor k.
–⃑ hat, aber s Einheiten lang ist.
3) Gib jenen Vektor an, der dieselbe Richtung wie AB
a) A(–8|3|6), B(–6|–3|12); k = 1,5; s = 4
c) A(15|–4|12), B(2|8|11); k = 2; s = 34
3_
|
|
|
|
b) A(7 5 –2), B(9 –9 –5); k = –0,6; s = 5
d) A(–17|9|–6), B(–6|1|10); k = –3; s = 2_3
8.51 Berechne den Winkel zwischen den Vektoren a⃑ und b⃑.
B
a) a⃑ =
() ( )
3
0
7
, b⃑ =
0
25
–5
b) a⃑ =
() ()
11
–5
–7
, b⃑ =
27
–5
45
c) a⃑ =
() ()
–8
–3
16
, b⃑ =
24
13
–2
8.52 Berechne die fehlende Koordinate, sodass die beiden Vektoren orthogonal sind.
A B
a) a⃑ =
D
C
() ()
5
–6
–9
, b⃑ =
bx
5
–5
b) a⃑ =
() ( )
()
5
2
az
, b⃑ =
8.53 Erkläre, welchen Winkel Vektoren der Form
einschließen.
4
–8
–2
ax
ay
0
c) a⃑ =
() ()
()
–2
–9
3
, b⃑ =
mit dem Basisvektor e–⃑3 =
8.54 Gib die folgenden Vektoren als Linearkombination
–⃑, HM
–⃑ und HG
–⃑ an.
der Vektoren HD
–
–
–
–⃑
1) AB⃑
2) AM⃑
3) BJ⃑
4) MI
3
by
5
0
0
1
H
G
F
E
I
J
D
C
M
A
A B
224
B
8.55 Mit einem Computerprogramm soll ein Turm konstruiert
z
werden, der aus 10 Würfeln mit einer Kantenlänge von
jeweils 2,5 Einheiten bestehen soll (siehe Abbildung).
Um den Turm zu modellieren, wird jeweils ein Würfel
5
B‘
so generiert, dass der Eckpunkt D seiner Grundfläche
im Ursprung eines dreidimensionalen Koordinaten1
systems liegt. Anschließend wird dieser Würfel mithilfe
10 1
5
y
eines Vektors an die gewünschte Position verschoben.
x 5
B
10
1) Gib jenen Vektor an, mit dessen Hilfe der Eckpunkt B
von Würfel 1 in den Eckpunkt B′ von Würfel 10 verschoben werden kann.
2) Bestimme die Koordinaten des Mittelpunkts M des Würfels 1 und gib den
Verschiebungsvektor zu M′ in Würfel 6 an.
3) Im Mittelpunkt der obersten Begrenzungsfläche des Turms soll eine senkrechte
Antenne errichtet werden, die eine Länge von 3 Einheiten hat. Von deren Spitze S
aus sollen vier Seile gespannt werden, die jeweils zu den äußeren Eckpunkten von
Würfel 9 und Würfel 10 führen. Bestimme deren Richtungsvektoren und berechne die
Gesamtlänge aller Seile.
Algebra und Geometrie
Vektoren
8.56 Zeige, dass die Vektoren b⃑, c⃑ und d⃑ normal auf a⃑ stehen. Welche Folgerung ergibt sich daraus?
a⃑ =
B
D
() () () ( )
2
3
–1
; b⃑ =
3
–1
3
; c⃑ =
1
5
17
; d⃑ =
–3
–2
–12
8.57 Berechne die fehlenden Koordinaten des Parallelogramms ABCD.
a) A(11|3|–10), B(–4|5|–4), C(–1|14|5), D b) A(2|–7|13), B(12|–5|3), C, D(7|–1|–17)
8.58 In einem Großraumbüro werden zwischen den Arbeitsplätzen
Trennwände in Form von rechtwinkligen Dreiecken eingesetzt.
–⃑
Die Hypotenuse eines Dreiecks ist durch den Vektor OP
festgelegt, der rechte Winkel liegt im Eckpunkt P′, der die
Projektion von P auf die xy-Ebene ist (Längen in Meter).
–⃑ an und berechne dessen Länge.
1) Gib den Vektor OP
2) Berechne den Flächeninhalt der Trennwand mithilfe der
Vektorrechnung.
B
z
3
A B
2,4
P
2
1
0,8
O
0,6
1
2
P‘
y
1
x
8.59 Berechne die beiden Schnittwinkel zwischen den Diagonalen des Vierecks ABCD.
a) A(7|–4|–10), B(–7|–6|12), C(–7|8|9), D(1|–1|6)
b) A(9|13|–4), B(–13|8|11), C(14|0|–9), D(–3|4|–3)
B
8.60 Berechne den Umfang, den Flächeninhalt und den Schwerpunkt des Dreiecks ABC.
a) A(12|5|–10), B(–4|–14|9), C(8|–11|3)
b) A(15|0|–17), B(–8|–3|–9), C(–1|17|–4)
B
S
8.61 Über dem Eingang des Louvre wurde eine quadratische
Glaspyramide errichtet. Legt man die xy-Ebene in die
Grundfläche und den Ursprung O in den Mittelpunkt M,
so hat die linke vordere Ecke die Koordinaten
D
A(17,7|–17,7|0) (Angaben in Meter).
M
Die Höhe der Pyramide beträgt 21,7 m.
A
B
1) Gib die Koordinaten der Punkte B, C, D und S an.
2) Ermittle mithilfe von Vektoren die Oberfläche der Pyramide.
3) Ermittle mithilfe von Vektoren den Winkel zwischen einer Seitenfläche und der
Grundfläche.
A B
C
8.62 Der Vektor a⃑ schließt mit der gegebenen Achse den Winkel φ ein. Berechne die fehlende
Koordinate auf zwei Dezimalstellen genau.
a) a⃑ =
()
3
ay
5
, φ = 60°, y-Achse b) a⃑ =
()
ax
6
–2
, φ = 40°, x-Achse c) a⃑ =
8.63 Ein Bücherregal soll an einer Wand montiert werden.
Die Koordinaten der Punkte in der abgebildeten
Skizze sind in Zentimeter angegeben:
A(40|120|180), C(0|320|180), D(0|120|180), E(0|120|255)
1) Gib die Koordinaten der Punkte B und G an.
2) Ermittle die Länge der Strecke AE und den
Winkel, den diese mit der Wand einschließt.
3) Ermittle die Koordinaten des Punkts F so, dass die
Strecke AF normal auf AE steht.
()
–8
7
az
B
, φ = 75°, z-Achse
z
A B
G
E
C
B
D
A
F
y
O
x
8.64 Für den Mittelpunkt der Verbindungsstrecke der
Mittelpunkte der Diagonalen eines Vierecks ABCD gilt: M = 1_4 · (A + B + C + D)
1) Zeige die Gültigkeit anhand des Vierecks A(2|9|11), B( 3|1|–7), C(–4|–8|2), D(–2|–3|0).
2) Beweise die Aussage allgemein.
Algebra und Geometrie
B
D
225
Vektoren
8.6 Vektorprodukt (Vektorielles Produkt, Kreuzprodukt)
C
8.65 1) Was erfordert weniger Kraft zum Zu- bzw. Herausdrehen einer
Schraubenmutter, den Schraubenschlüssel so wie in der
Abbildung oder näher bei der Mutter zu halten?
2) Überlege, in welche Richtung sich die Mutter jeweils bewegt,
wenn der Schraubenschlüssel im bzw. gegen den Uhrzeigersinn
gedreht wird.
In Abschnitt 8.3 wurde das Skalarprodukt verwendet, um unter anderem die an einem Körper,
der entlang einer Strecke bewegt wird, verrichtete Arbeit zu ermitteln. Zur Untersuchung
der Auswirkungen von Drehbewegungen benötigt man einen weiteren Begriff aus der
Vektorrechnung.
Ein Moment ist das Maß für die Wirkung einer Kraft. Aus dem naturwissenschaftlichen
–⃑ bekannt. Übt man zum Beispiel mithilfe eines Korkenziehers
Unterricht ist das Drehmoment M
Kraft auf einen Korken aus, so bewegt sich das Gewinde entweder in den Korken hinein oder
aus dem Korken heraus, je nachdem, in welche Richtung der Korkenzieher gedreht wird. Diese
Wirkung, also das Drehmoment, ist daher eine gerichtete Größe. Das Drehmoment kann
anhand der Bewegung einer Kreisscheibe veranschaulicht werden:
F
F
F
r
r
Die Scheibe dreht sich nicht,
es ist keine Wirkung
vorhanden.
s
M
Die Scheibe beginnt sich zu
–⃑ ist
drehen, die Wirkung M
erkennbar und messbar.
r
M
s
Die Scheibe dreht sich
–⃑ ist
nun schneller, M
größer.
{
–⃑ sind gerichtete Größen. Der Vektor M
–⃑ steht sowohl auf
F⃑, r⃑ und M
–⃑ |
den Vektor F⃑ als auch auf den Vektor r⃑ normal. Sein Betrag | M
hängt von | F⃑ | und von s = | r⃑ | · sin(φ) ab. Für das Drehmoment gilt:
–⃑ = | r⃑ | · sin(φ) · | F⃑ | · n–⃑, n–⃑ ... Einheitsvektor, normal auf r⃑ und F⃑
M
0
M
r
n0
0
(vergleiche Rechte-Hand-Regel)
–⃑|
|M
Allgemein gilt für zwei Vektoren a⃑ und b⃑ :
Der Vektor c⃑, der sowohl auf a⃑ als auch auf b⃑ normal steht, wird
Vektorprodukt, Kreuzprodukt oder vektorielles Produkt der
Vektoren a⃑ und b⃑ genannt.
Man schreibt: c⃑ = a⃑ × b⃑ [sprich: „a kreuz b“]
Für den Betrag bzw. für die Länge von c⃑ gilt: | c⃑ | = | a⃑ | · | b⃑ | · sin(φ)
F
a b
b
a b
a
Vergleicht man diese Formel mit der trigonometrischen
a · b · sin(φ)
Flächenformel A = _______
(vgl. Abschnitt 6.1), so sieht man, dass der Betrag des Vektors c⃑
2
der Maßzahl des Flächeninhalts des von den Vektoren a⃑ und b⃑ aufgespannten Parallelogramms
entspricht.
Unter Verwendung dieser Schreibweise für das Vektorprodukt ergibt sich für das Drehmoment:
–⃑ = „Kraftarm x Kraft“ = r⃑ × F⃑
M
226
Algebra und Geometrie
Vektoren
Vektorprodukt (vektorielles Produkt, Kreuzprodukt)
Das Vektorprodukt von zwei Vektoren a⃑ und b⃑ ergibt einen Vektor c⃑ = a⃑ × b⃑ , für den gilt:
• | c⃑ | = | a⃑ | · | b⃑ | · sin(φ) ... Maßzahl des Flächeninhalts des von a⃑ und b⃑ aufgespannten
Parallelogramms
• c⃑ steht auf a⃑ und auf b⃑ normal; a⃑, b⃑ und c⃑ = a⃑ × b⃑ bilden ein Rechtssystem.
Das Vektorprodukt kann auch in Koordinatenschreibweise angegeben werden.
Berechnung des Vektorprodukts in Koordinatenschreibweise
a⃑ × b⃑ =
() () (
ax
ay
az
bx
by
bz
×
=
ay · bz – az · by
az · bx – ax · bz
ax · by – ay · bx
)
Um sich diese Formel leichter zu merken, gibt es verschiedene Merkhilfen, zum Beispiel:
• Berechnung mithilfe von Unterdeterminanten:
• Komponentenweise Multiplikation:
In der Determinante
ax
bx
aybz – azby
ay by
– by
ay +
für die Berechnung
a
z bz
azbx – axbz
– bz =
az +
ax
bx
der x-Komponente
a
b
ax +
– bx
axby – aybx
ay × by = – x x
az bz
ay
by
„fehlen“ die
az
bz
ax bx
x-Komponenten, usw.
() ()
(
)
() ()
( )
| |
| |
|a b |
y
8.66 1) Berechne das Vektorprodukt c⃑ der Vektoren a⃑ =
()
3
2
–1
und b⃑ =
()
–2
5
1
y
.
B
D
2) Zeige, dass der Vektor c⃑ auf die Vektoren a⃑ und b⃑ normal steht.
Lösung:
1) c⃑ = a⃑ × b⃑ =
2) c⃑ · a⃑ =
c⃑ · b⃑ =
()()(
( )( )
( )( )
3
2
–1
×
–2
5
1
=
2 · 1 – 5 · (–1)
(–2) · (–1) – 3 · 1
3 · 5 – (–2) · 2
)()
=
7
–1
19
7
–1
19
·
3
2
–1
= 7 · 3 + (–1) · 2 + 19 · (–1) = 21 – 2 – 19 = 0
7
–1
19
·
–2
5
1
= 7 · (–2) + (–1) · 5 + 19 · 1 = –14 – 5 + 19 = 0
Das Skalarprodukt hat den Wert null, die Vektoren stehen normal aufeinander.
Eigenschaften des Vektorprodukts:
• Vertauscht man beim Bilden des Vektorprodukts c⃑ = a⃑ × b⃑ die Reihenfolge der Vektoren, so
wird mit b⃑ × a⃑ ein Linkssystem gebildet. Man erhält den Gegenvektor von c⃑.
Das Vektorprodukt ist also nicht kommutativ, es gilt jedoch:
a⃑ × b⃑ = –b⃑ × a⃑
a b
a⃑ × b⃑ =
b⃑ × a⃑ =
( ) ( ) ()
()()()
1
–3
0
×
2
0
–1
=
2
0
–1
×
1
–3
0
=
3
1
6
a
–3
–1
–6
• Es gilt das Distributivgesetz:
• a⃑ × a⃑ = o⃑
b
a⃑ × (b⃑ + c⃑) = a⃑ × b⃑ + a⃑ × c⃑
Algebra und Geometrie
b a
227
Vektoren
Flächen- und Volumenberechnungen mithilfe des Vektorprodukts
Gemäß der Definition für das Vektorprodukt gilt |a⃑ × b⃑| = | a⃑ | · | b⃑ | · sin(φ), wobei φ der
Winkel zwischen a⃑ und b⃑ ist und 0° < φ < 180° gilt. Dieser Betrag entspricht der Maßzahl des
Flächeninhalts eines von a⃑ und b⃑ aufgespannten Parallelogramms: AP = |a⃑ × b⃑|
Somit gilt für den Flächeninhalt eines von a⃑ und b⃑ aufgespannten Dreiecks: A = _1 · |a⃑ × b⃑|
D
2
Flächeninhalt eines von a⃑ und b⃑ aufgespannten Parallelogramms: AP = |a⃑ × b⃑|
Flächeninhalt eines von a⃑ und b⃑ aufgespannten Dreiecks: AD = 1_2 · |a⃑ × b⃑|
B
() ()
)| |( ) ( )| |(
1
–4
3
8.67 Berechne den Flächeninhalt des von a⃑ =
Lösung:
A = 1_2 · |a⃑ × b⃑| =
|( )|
–16
–13
–12
|(
ay · bz – az · by
az · bx – ax · bz
ax · by – ay · bx
= 1_2 ·
1
–4
3
×
–5
8
–2
und b⃑ =
–5
8
–2
aufgespannten Dreiecks.
–4 · (–2) – 3 · 8
3 · (–5) – 1 · (–2)
1 · 8 – (–4) · (–5)
= 1_2 ·
)| |( )|
= 1_2 ·
–16
–13
–12
= √––––––––––––––––––––
(–16)2 + (–13)2 + (–12)2 = √––––
569 ⇒ A = _12 · √––––
569 = 11,926...
Der Flächeninhalt beträgt rund 11,9 E2.
Unter einem Parallelepiped – auch Spat genannt – versteht man einen Körper,
der von sechs paarweise kongruenten, in parallelen Ebenen liegenden Parallelogrammen begrenzt wird. Das altgriechische Wort „epipedon“ bedeutet so viel
wie „Fläche“. Die Bezeichnung Spat für ein Parallelepiped bezieht sich auf das
Mineral Kalkspat, das in der abgebildeten Form auskristallisiert. Dieser Körper
wird durch drei Vektoren im Raum aufgespannt, sein Volumen entspricht dem
Betrag des Spatprodukts (a⃑ , b⃑, c⃑) = (a⃑ × b⃑) · c⃑ = (b⃑ × c⃑) · a⃑ = (c⃑ × a⃑) · b⃑.
Dieser Wert ist positiv, wenn es sich bei den drei Vektoren um ein Rechtssystem handelt, sonst
ist er negativ. Liegen die drei Vektoren in einer Ebene, so ist das Spatprodukt gleich null.
Volumen eines Parallelepipeds
V = |(a⃑ × b⃑) · c⃑| = |(b⃑ × c⃑) · a⃑| = |(c⃑ × a⃑) · b⃑|
h
c
Volumen eines Tetraeders
V = 1_6 · |(a⃑ × b⃑) · c⃑|
b
a
a
B
c
b
() () ()
|(( ) ( )) ( )| |( ) ( )|
8.68 Berechne das Volumen des von a⃑ =
Lösung:
V = |(a⃑ × b⃑) · c⃑| =
3
5
–1
×
9
–6
6
·
–2
0
–7
3
5
–1
, b⃑ =
=
24
–27
–63
9
–6
6
·
und c⃑ =
–2
0
–7
aufgespannten Körpers.
= |–48 + 441| = 393
Das Volumen beträgt 393 E3.
228
–2
0
–7
Algebra und Geometrie
Vektoren
Technologieeinsatz: Vektorprodukt
TE
TI-Nspire
8.69 Für eine Skulptur wird eine Marmorsäule angefertigt
(vergleiche Abbildung). Die Koordinaten der Eckpunkte
A(0|0|0), B(45|0|0), D(20|18|0) und E(5|0|90) sind gegeben
(Maße in cm).
1) Ermittle den Flächeninhalt der Grundfläche der Säule.
2) Berechne den Winkel, den die Kante AB mit der Kante
AE einschließt.
3) Die Dichte des verwendeten Marmors beträgt
g
ρ = 2,9 ___
3 . Berechne die Masse der Säule in kg.
B
z
E
A
x
B
D
y
cm
Lösung:
Vektoren werden gespeichert:
• Die –
–
–
1)
a⃑ = AB⃑, b⃑ = AD⃑ und c⃑ = AE⃑
• Die Grundfläche ist ein Parallelogramm,
dessen Flächeninhalt f = |a⃑ × b⃑| beträgt.
Die Säule hat eine Grundfläche
von 810 cm2.
Für die Berechnung des Vektorprodukts
steht der Befehl crossP( zur Verfügung,
der eingetippt oder über das Menü
7: Matrix und Vektor, C: Vektor,
2: Kreuzprodukt aufgerufen werden
kann. Den Betrag des Vektors a⃑ × b⃑
erhält man mithilfe des Befehls norm(
im Menü 7: Matrix und Vektoren,
7: Normen, 1: Norm.
• Das Skalarprodukt wird mithilfe des
2)
Befehls dotP( ermittelt, das Winkelmaß
Grad muss eingestellt sein.
Der Winkel zwischen den Kanten AB
und AE beträgt rund 86,8°.
g
kg
= 0,0029 ___
• ρ = 2,9 ___
cm
cm
• Die Säule hat die Form eines
3)
3
Die Säule hat eine Masse von rund
211 kg.
3
Parallelepipeds. Beachte bei der Eingabe
der Formel, dass |(a⃑ × b⃑)| · c⃑ ein Skalar
ist. Der Betrag einer Zahl kann nicht
mithilfe von norm( ermittelt werden,
sondern wird mit dem Befehl abs( aus
dem Menü 2: Zahl, 9: Komplex,
5: Betrag ermittelt.
Algebra und Geometrie
229
Vektoren
–⃑ × BC
–⃑.
8.70 1) Ermittle das Vektorprodukt AB
2) Berechne den Betrag des Vektorprodukts.
a) A(–1|3|2), B(–4|3|9), C(4|28|24)
c) A(6|–3|–4), B(–2|10|12), C(2|23|10)
b) A(2|4|–4), B(12|–2|7), C(12|–15|15)
d) A(5|6|5), B(9|0|–3), C(–2|–13|14)
B
A
8.71 Gib die Länge und die Richtung des Vektors a⃑ × b⃑ an, wenn der Vektor a⃑ in Richtung der
negativen x-Achse und b⃑ in Richtung der positiven y-Achse verläuft.
C
A
D
C D
B C
8.72 Veranschauliche durch eine Skizze und beweise rechnerisch:
Liegen die Vektoren a⃑ und b⃑ in der xy-Ebene, so verläuft a⃑ × b⃑ parallel zur z-Achse.
8.73 Ändert sich das Vorzeichen von a⃑ × b⃑, wenn die Vorzeichen aller Komponenten von
1) a⃑
2) b⃑
3) a⃑ und b⃑
geändert werden? Begründe deine Antworten.
8.74 Vergleiche die Ergebnisse (a⃑ × b⃑) × c⃑ und a⃑ × (b⃑ × c⃑) für a⃑ =
beschreibe, was dir auffällt.
a) a⃑ =
, b⃑ =
8
–3
8
, c⃑ =
10
–1
2
und
() ()
1
–3
–4
, b⃑ =
–2
7
–6
b) a⃑ =
( ) ()
–9
5
–9
, b⃑ =
0
3
0
c) a⃑ =
() ()
6
–1
–2
, b⃑ =
9
–3
–2
8.76 Berechne das Volumen des Parallelepipeds, das von den Vektoren a⃑, b⃑ und c⃑ aufgespannt
wird.
B
a) a⃑ =
() () ( )
–2
6
–3
, b⃑ =
1
0
–8
, c⃑ =
11
4
–13
b) a⃑ =
() ( ) ( )
0
9
9
, b⃑ =
–2
11
–8
, c⃑ =
–7
5
–14
8.77 Berechne das Volumen des Tetraeders, der von den Vektoren a⃑, b⃑ und c⃑ aufgespannt wird.
B
a) a⃑ =
A B
2
4
–1
8.75 Berechne den Flächeninhalt 1) des Parallelogramms, 2) des Dreiecks, das von den
Vektoren a⃑ und b⃑ aufgespannt wird.
B
A
() () ()
C
() () ()
5
–7
9
, b⃑ =
–1
10
–6
, c⃑ =
12
–5
15
b) a⃑ =
() () ()
–2
–7
–5
, b⃑ =
22
–8
0
, c⃑ =
–5
8
–3
8.78 Ein Quader ABCDEFGH hat die Kantenlängen a, b und h.
1) Gib die Koordinaten seiner Eckpunkte an, wenn A im Koordinatenursprung liegt und
kein Eckpunkt negative Koordinaten hat.
2) Dokumentiere nachweislich, wie mithilfe der Vektorrechnung die Volumenformel
V = a · b · h hergeleitet werden kann.
8.79 Spezielle Eiswürfel haben die Form von Parallelepipeden.
Die parallelogrammförmige Basisfläche wird durch die
Vektoren a⃑ =
()
1
1
0
und b⃑ =
()
0
2,5
0
aufgespannt (Maße in cm).
Ein Eiswürfel ist 1,5 cm hoch, die Deckfläche ist im Vergleich
zur Grundfläche um 0,5 cm in y-Richtung verschoben.
1) Lege den Eckpunkt der Basis des Eiswürfels in den
Ursprung eines Koordinatensystems. Alle Basiseckpunkte haben positive Koordinaten.
Ermittle alle weiteren Eckpunkte des Parallelepipeds.
2) Eine Gussform mit der Masse mG = 50 g fasst 24 solcher Eiswürfel. Berechne die
kg
Gesamtmasse der gefüllten Gussform in kg (Dichte von Eis: ρ = 0,918 ___3 ).
dm
230
Algebra und Geometrie
Vektoren
8.7 Anwendungen der Vektorrechnung im ℝ3
Für das Rechnen mit Kräften gelten im ℝ3 die gleichen Regeln wie im ℝ2. Zusätzlich wird auch
das Vektorprodukt bei einigen physikalischen Größen verwendet:
z
r von einem Drehpunkt an,
• Greift eine Kraft F⃑ in einem Abstand
–
so erzeugt sie ein Drehmoment M⃑ (vgl. Abschnitt 8.6):
–⃑ = r⃑ × F⃑
M
L
⃑
• Der Impuls p ist das Produkt aus der Masse m eines Massepunkts
⃑ = m · v⃑
und der Geschwindigkeit v⃑ : p
r
x
p
Wirkt ein Impuls auf einen Massepunkt in einem Abstand r von
m
einem Drehpunkt, so entsteht ein Drehimpuls: L⃑ = r⃑ × p⃑
Magnetfeld
• Bewegt sich eine elektrische Ladung q mit der Geschwindigkeit
–
Stromrichtung
v⃑ durch ein Magnetfeld mit der magnetischen Feldstärke B⃑, so
wird sie durch die Lorentzkraft F–⃑L abgelenkt (Hendrik Lorentz,
niederländischer Physiker, 1853 – 1928). Es gilt: F–⃑L = q · (v⃑ × B–⃑)
8.80 Im Raum greifen die beiden Kräfte F–⃑1 =
()
20
0
35
und F–⃑2 =
()
0
21
15
FL
z
+
0
21
15
FR
F1
10
20
21
50
=
A B
F2
() () ()
20
0
35
v
B
im
selben Punkt an. Ermittle den Vektor und den Betrag der
resultierenden Kraft und berechne den Winkel, den sie mit
der xy-Ebene einschließt (Angaben in N).
Lösung:
F–⃑R = F–⃑1 + F–⃑2 =
y
F2
y
0
2
2
2
––––––––––––––
FR = |F–⃑|
R = √ FRx + FRy + FRz = 57,801... N ≈ 58 N
10
10
FRp
x
1. Möglichkeit: Winkel zwischen zwei Vektoren
()()
20
20
21 · 21
F–⃑R · F–Rp⃑
0
50
841
______
_______
= 0,501...
cos(φ) = –⃑| –⃑| = 57,801... · 29 = _______
1 676,240...
|F · |F
R
• F–Rp⃑ =
Rp
Projektion von F–⃑R auf die
xy-Ebene
φ = 59,886...° ≈ 60°
2. Möglichkeit: Winkel im rechtwinkligen Dreieck
F
F
50
sin(φ) = __Rz ⇒ φ = arcsin __Rz = arcsin _____
( )
FR
( 57,801... )
FR
φ = 59,886...° ≈ 60°
()
20
21
0
8.81 Im Raum greifen zwei Kräfte F–⃑1 und F–⃑2 im selben Punkt an. Berechne die resultierende
Kraft F–⃑R und den Winkel, den F–⃑R mit der xy-Ebene einschließt (Angabe in N).
1,2
1 250
55
720
120
0
a) F–⃑ = 30 , F–⃑ = 0
b) F–⃑ = 2 , F–⃑ = 0
c) F–⃑ = 3 090 , F–⃑ = 2 105
1
() ()
0
2
() ()
1
190
0,2
2
1,5
1
A B
( ) ( )
2
478
3 180
8.82 Eine Kraft schließt mit der yz-Ebene den Winkel ε und mit der xy-Ebene den Winkel φ
ein. Zerlege die Kraft in ihre x-, y- und z-Komponente.
a) F = 790 N, ε = 20°, φ = 40°
b) F = 4 070 N, ε = 85°, φ = 110°
A B
8.83 Zerlege die gegebene Kraft in die vorgegebenen Richtungen (Kräfte in N).
A B
a) ⃑F =
( ) () () ()
45
20
35
, a⃑ =
1
0
1
, b⃑ =
0
1
0
, c⃑ =
2
1
0
b) ⃑F =
( ) () () ()
720
0
480
Algebra und Geometrie
, a⃑ =
–1
1
2
, b⃑ =
1
0
–1
, c⃑ =
0
–1
2
231
Vektoren
A B C
8.84 Ein Wasserkessel mit einem Gewicht von 120 N soll an einem regelmäßigen Dreibein
aufgehängt werden. Die Grundfläche des Dreibeins ist ein gleichseitiges Dreieck mit
einer Seitenlänge s = 3 m, die Höhe beträgt h = 2 m.
1) Fertige eine Skizze an und beschreibe die Zusammenhänge.
2) Berechne die Kräfte, die in den Beinen wirken müssen.
Lösung:
1)
z
Da die Beine gleich lang sind, hängt
der Kessel über dem Schwerpunkt
des gleichseitigen Dreiecks. Der
Schwerpunkt liegt in diesem Fall im
Drittelpunkt der Höhe hD.
Das Dreibein wird in ein
Koordinatensystem gelegt, wobei
der Schwerpunkt im Ursprung liegt.
F1
F2
F3
FG
a
P1
b
s
s
P2
c
hD
O
y
s
x
P3
2) hD = _2s · √––
3 = 3_2 · √––
3m
• Bestimmen der Koordinaten der
Eckpunkte
( | |0) = P (–3_2|–1_2 · √––3 |0)
3 |0), P (0|√––
3 |0)
P ( 3_2|– 1_2 · √––
hD
P1 – _2s – __
3
1
2
3
b⃑ =
–1,5
–0,5 · √––
3
–2
( )
( ––) ( ––)
–⃑ =
a⃑ = SP
1
1,5
–0,5 · √ 3
–2
, c⃑ =
• Da die Kraftvektoren parallel zu
den Vektoren der Stäbe sind,
haben sie die gleiche Richtung
wie die Stäbe.
0
√3
–2
F–G⃑ + F–⃑1 + F–⃑2 + F–⃑3 = o⃑ ⇒ –F–G⃑ = F–⃑1 + F–⃑2 + F–⃑3
–1,5
–0,5 · √––
3
–2
1,5
–0,5 · √––
3
–2
• Die Kräfte müssen im
Gleichgewicht sein.
• Die Linearkombination aus
den Kräften führt auf ein
Gleichungssystem, das mit
Technologie gelöst werden kann.
() ( ) ( ) ()
0
0
120
=r·
+s·
+t·
0
3
√––
–2
r = s = t = –20
F–⃑1 =
( ––) ( ––) ( ––)
30
10 · √ 3
40
, F–⃑2 =
–30
10 · √ 3
40
, F–⃑3 =
0
–20 · √ 3
40
F1 = F2 = F3 = 52,951... N ≈ 53 N
• Da die Vektoren gleich lang sind,
sind auch die Kräfte gleich groß.
A B C
8.85 Eine Last mit der Gewichtskraft F–G⃑ wird an drei Stützen aufgehängt (siehe Abbildung,
Maße in Meter). Berechne die Richtungen und die Beträge der Stützkräfte.
a) FG = 130 N
b) FG = 2,85 kN
z
z
3
5
s1
s3
s1 FG
1
x
232
O
FG
s3
s2
s2
1
1
y
x
Algebra und Geometrie
O
1
y
Vektoren
8.86 Zum Fotografieren von Naturmotiven wird eine Kamera
mit einer Masse von 950 g im Punkt P(0|0|60) stabil auf
einem dreibeinigen Stativ befestigt. Aufgrund von
Unebenheiten im Gelände sind die Beine unterschiedlich
lang. Die Berührpunkte der Stativbeine mit dem
Untergrund haben die Koordinaten A(–30|–60|0),
B(20|–30|0) und C(–40|30|20) (Maße in cm).
1) Fertige eine Skizze der Kräfte an, die wirken, um die Kamera zu tragen.
2) Ermittle die Richtungsvektoren und die Längen der Stativbeine s1, s2 und s3.
3) Berechne die Kräfte, die in den Stativbeinen wirken.
A B
Anwendungen des Vektorprodukts
–⃑ = r⃑ × F⃑ und M
–⃑ = F⃑ × r⃑.
8.87 Beschreibe den Unterschied zwischen den Drehmomenten M
1
2
–⃑ , r⃑ oder F⃑ und
8.88 Trage die Richtung des fehlenden Vektors M
F
die Drehrichtung ein. Verwende die Rechte-Hand-Regel.
r
1)
2)
3)
F
r
C
C
r
M
F
M
M
8.89 An einem Massepunkt im Punkt P(3|11|−7) wirkt eine Kraft F. Berechne das
Drehmoment bezüglich des Koordinatenursprungs (Längen in m, Kräfte in N).
a) F⃑ = (34, 2, –19)
b) F⃑ = (–17, 10, 18)
8.90 Bei starkem Wind wirkt auf die Ampel eine Kraft F⃑ =
( )
120
285
0
B
z
N.
A B
F
8.91 An einen Körper, dessen Massenmittelpunkt im Ursprung
liegt, greift im Punkt P(rx|ry|rz) eine Kraft F⃑ in Richtung der
y-Achse an. Von welchen Koordinaten von P hängt das
dabei wirkende Drehmoment ab?
4m
Berechne das im Fußpunkt der Stange wirkende Drehmoment.
A
C
3m
x
y
8.92 Auf vielen Spielplätzen gibt es Karusselle, die durch Muskelkraft in Drehbewegung
versetzt werden können. Der Mittelpunkt der Drehscheibe eines solchen Karussells
befindet sich im Punkt A(5|3|1). Ein Erwachsener übt am Rand des Karussells im Punkt
P(5,6|3,8|1) gegen den Uhrzeigersinn einen Kraftstoß aus. Dadurch dreht sich das
__ . Die Gesamtmasse des Karussells
Karussell mit der Tangentialgeschwindigkeit v = 4,2 m
s
und der Kinder beträgt m = 150 kg (Längen in Meter).
1) Ermittle den Vektor des Karussellradius r⃑ = –
AP⃑ sowie die Richtung der Tangentialgeschwindigkeit.
2) Gib den Impulsvektor p⃑ sowie die Richtung und den Betrag des Drehimpulses L⃑
bezüglich des Punkts A an.
__ in
8.93 Bei einem Experiment bewegen sich Protonen (q = 1,602 · 10–19 C) mit v = 1,5 · 108 m
s
A B
A B
D
einem Teilchenbeschleuniger in x-Richtung. Es wirkt ein Magnetfeld mit der Magnetfeldstärke B = 0,5 T (Tesla) abwechselnd in positive und negative z-Richtung.
1) Ermittle die Richtung und den Betrag der Lorentzkraft in beiden Fällen.
2) Argumentiere, ob es sich auf die Ergebnisse auswirkt, wenn mit F–⃑L = (q · v⃑) × B⃑ bzw.
F–⃑L = v⃑ × (q · B⃑ ) gerechnet wird. Überprüfe deine Argumentation rechnerisch.
Algebra und Geometrie
233
Vektoren
8.8 Geraden in der Ebene
8.8.1 Parameterdarstellung
B C
8.94 Zeichne die Gerade y = x + 5 in ein Koordinatensystem ein. Beschreibe, wie man einen
Vektor in Richtung der Geraden ermitteln kann.
y
X
Eine Gerade kann in der Ebene mithilfe eines festen Punkts und eines
a
P
Vektors, dem so genannten Richtungsvektor, beschrieben werden.
g
OX
OP
Man erreicht jeden beliebigen Punkt X(x|y) einer Geraden, wenn
–⃑ eines Punkts P(x |y ) ein Vielfaches eines
x
man zum Ortsvektor OP
P P
O
ax
–⃑ = OP
–⃑ + t · ⃑a
addiert: g: OX
t∊ℝ ... Parameter
Richtungsvektors ⃑a =
ay
Da der Punkt und der Richtungsvektor beliebig gewählt werden können, gibt es unendlich viele
Parameterdarstellungen für eine Gerade.
Mithilfe des Strahlensatzes erkennt man, dass man einen Richtungsvektor der
Geraden auch mithilfe der Steigung k der Geraden darstellen kann:
a
ay
1
ax
1
k
ay =
⃑a =
__
k
ay
ax
1 a
()
( ) ( ) ()
() () ( )
() () ( ) () ( ) ()
() () ( ) () ( ) ( )
()
()
( )( )
x
3
–1
Gerade g:
=
+t·
; Setzt man für den Parameter t die
y
4
2
Werte 2 bzw –1,5 ein, so erhält man die Punkte A und B.
x
3
–1
3
–2
1
=
+2·
=
+
=
⇒ A(1|8)
t = 2:
y
4
2
4
4
8
t = –1,5:
x
3
–1
3
1,5
4,5
=
+ (–1,5) ·
=
+
=
⇒ B(4,5|1)
y
4
2
4
–3
1
–1
paralleler
Für die Steigung k der Geraden wird ein zu
2
Richtungsvektor der Form
x
8
7
6
y g
A
2. a
5
a
4
1
P
3
k = -2
-1,5 . a
2
B
1
x
0
1
2
3
4
5
1
–1
1
ermittelt:
⇒ k = –2
k
2
–2
Parameterdarstellung einer Geraden in der Ebene
–⃑ = OP
–⃑ + t · ⃑a bzw. x = xP + t · ax mit t∊ℝ kurz: g: X = P + t · ⃑a
g: OX
y
yP
ay
1
Darstellung eines Richtungsvektors einer Geraden mithilfe der Steigung k: ⃑a =
k
() ( ) ( )
B C
()
() () ()
x
3
1
=
+t· .
y
2
4
Ermittle die fehlende Koordinate. Beschreibe deinen Lösungsweg.
Lösung:
Liegt der Punkt A auf der Geraden g, so
x
3
1
5
3
1
=
+t·
⇒
=
+t·
muss der Parameter t sowohl für die x- als
y
2
4
yA
2
4
auch für die y-Koordinate den gleichen Wert
5=3+t ⇒ t=2
annehmen. Die erste Gleichung liefert t = 2;
yA = 2 + 4t
dieser Wert wird in die zweite Gleichung
yA = 2 + 4 · 2 = 10 ⇒ A(5|10)
eingesetzt.
8.95 Der Punkt A(5|yA) liegt auf der Geraden g:
() () () ( ) () ()
234
Algebra und Geometrie
6
Vektoren
8.96 Ermittle eine Parameterdarstellung der Geraden g, die durch die Punkte A(3|7) und
B(6|−2) verläuft. Beschreibe deinen Lösungsweg.
Lösung:
–⃑ = 6 – 3 = 3 1
AB
–2 – 7
–9 –3
B C
Der Vektor –
AB⃑ ist ein Richtungsvektor der
–⃑ parallele
Geraden g, daher ist auch der zu AB
Vektor ein Richtungsvektor von g.
Als Punkt der Geraden kann A oder B gewählt
werden.
( ) ( )( )
() ( )
–⃑ = 3 + t · 1
g: OX
7
–3
Lagebeziehungen zwischen Geraden in der Ebene
Zwei Geraden in der Ebene können parallel oder ident sein oder einen Schnittpunkt haben.
Zur Berechnung des Schnittpunkts werden die Parameterdarstellungen komponentenweise
gleichgesetzt. Die Anzahl der Lösungen des entstehenden Gleichungssystems hängt von der
gegenseitigen Lage ab.
• Existiert ein Schnittpunkt, so ist das Gleichungssystem eindeutig lösbar.
–⃑ =
g: OX
( ) ()
() ()
–1
3
–⃑ = 4 + s · –1
+ r · ; h: OX
2
1
2
–1
5
h
g
4
g ∩ h: I: –1 + 3r = 4 – s
II: 2 + r = –1 + 2s
r = 1, s = 2
–⃑ = –1 + 1 · 3 = 2 bzw. OS
–⃑ = 4 + 2 · –1 = 2
OS
2
1
3
2
3
–1
( ) () ()
y
S
3
Pg
2
1
x
( ) ( ) ()
-1 0
-1
1
2
3
4
Ph
5
Der Schnittpunkt hat die Koordinaten S(2|3).
• Sind die Geraden parallel bzw. ident, so hat das Gleichungssystem
y
keine bzw. unendlich viele Lösungen.
–⃑ =
g: OX
() ( )
() ()
() ()
1
2
–⃑ = 5 + s · –1 ; k: OX
–⃑ = 4 + s · –1
+r·
; h: OX
5
4
4
–8
–3
–7
g ∩ h:
I: 1 + 2r = 5 – s | · 4
+
II: 5 – 8r = –3 + 4s
9
= 17
Das Gleichungssystem hat
keine Lösung, die Geraden
sind zueinander parallel.
}
g ∩ k:
I: 1 + 2r = 4 – s | · 4
+
II: 5 – 8r = –7 + 4s
9
=9
Das Gleichungssystem hat
unendlich viele Lösungen,
die Geraden sind ident.
Pg
1
0
}
In beiden Fällen sind die Richtungsvektoren zueinander parallel:
5
x
2
4
6
Ph
-5
Pk
h
g
( )( )
–1
2
4
–8
8.97 Berechne die Koordinaten der Punkte der Geraden g mit den Parametern t1 und t2.
–⃑ = 9 + t · –2 ; t = 3, t = –5
–⃑ = 3 + t · 8 ; t = –1, t = 1_
a) g: OX
b) g: OX
1
2
2 4
5
3 1
–8
–1
B
8.98 Gib die Gleichung der Geraden g, auf der die beiden Punkte liegen, in Parameterform an.
a) g: A(6|–2), B(3|0)
b) g: M(–9|4), N(5|6)
c) g: R(15|–11), S(–23|19)
B
() ()
( ) ()
Algebra und Geometrie
235
Vektoren
A
C D
D
8.99 1) Gib die Gleichung der abgebildeten
Geraden in Parameterdarstellung
an, verwende dabei den Punkt A
und den Vektor ⃑a.
2) Erkläre das Prinzip der
Parameterdarstellung anhand der
abgebildeten Punkte P1, P2 und P3.
Gib für jeden dieser Punkte den
Parameter t an.
y
P3
5
P2
A
P1
1
x
-5
-1
O
1
5
8.100 Welche der folgenden Aussagen sind wahr, welche falsch? Begründe deine Antworten.
1) Geraden mit gleichen Richtungsvektoren sind ident.
2) Haben zwei Geraden verschiedene Richtungsvektoren, so haben sie einen
Schnittpunkt.
3) Zwei Geraden sind parallel, wenn ihre Richtungsvektoren parallel sind.
B
8.101 Gib die Gleichungen der Geraden in Parameterdarstellung an und berechne den
Schnittpunkt.
a) g1: A(6|7), B(12|–2), g2: C(–4|6), D(6|–4) b) g1: A(1,5|–9), B(9,5|–7), g2: C(5|7), D(–2|4)
A B
8.102 Für ein Geocaching im Schulhof wird der abgebildete Plan entworfen (Maße in Meter).
Es gilt: A(0|0), D(30,2|35,4) ... Ecken des Schulhofs
y
40
B(28|16,5)
... Baum
D
35
C(2,5|30)
... Trinkbrunnen
C
30
Die Dose mit dem Logbuch befindet sich
Trinkbrunnen
25
im Schnittpunkt der Strecke AB mit der
Streckensymmetrale von CD.
20
Baum
1) Gib die Gleichung der Geraden durch AB sowie die
B
15
Gleichung der Streckensymmetrale von CD jeweils in
E
10
Parameterdarstellung an.
5
2) Ermittle die Koordinaten des Punkts E, an dem sich
x
das Logbuch befindet.
10
15
20
25
30
35
0 A
5
A B C
8.103 Lisa und Sylvia gehen in einer nahegelegenen ebenen
Parkanlage laufen. Alle Wege sind geradlinig.
Lisa läuft vom Südtor S(995|125) direkt zum Nordtor
N(2 795|2 525). Sylvia beginnt ihren Lauf am Westtor
W(140|2 317). Ihr direkter Weg zum Osttor hat die
–⃑ = 15 (Angaben in Meter).
Richtung w
–8
1) Stelle jeweils eine Parameterdarstellung der
Trägergeraden der Laufwege von Lisa und Sylvia auf.
2) Berechne, an welchem Punkt und in welchem Winkel sich die beiden Wege kreuzen.
__ , Sylvia legt im Mittel
3) Lisa bewegt sich mit einer mittleren Geschwindigkeit von 9 km
h
pro Minute eine Strecke von 125 m zurück. Gib an, ob die beiden Freundinnen
einander an der Wegkreuzung treffen, wenn sie gleichzeitig starten. Beschreibe deine
Vorgehensweise.
4) Sylvia benötigt rund 31 Minuten, um vom Westtor zum Osttor zu gelangen. Ermittle
die Koordinaten des Osttors. Runde auf ganze Meter.
()
236
a
Algebra und Geometrie
Vektoren
8.8.2 Parameterfreie Darstellung
( ) ()
–⃑ = –8 + t · 4 grafisch dar. Ermittle den Anstieg der Geraden
8.104 Stelle die Gerade g: OX
–2
3
und den Schnittpunkt mit der y-Achse aus der Zeichnung.
Erkläre den Zusammenhang zwischen dem Richtungsvektor und dem Steigungsdreieck
einer Geraden.
B
D
Eine in Parameterdarstellung angegebene Gerade kann parameterfrei dargestellt werden, indem
man den Parameter eliminiert.
–⃑ = 5 + t · 2 soll in der Form y = k · x + d angegeben werden.
Die Gerade g: OX
–3
3
I:
x = 5 + 2t
• Die Gleichung wird in x- und y-Koordinaten „zerlegt“.
II:
y = –3 + 3t
I*: 3x = 15 + 6t
• Anschließend wird so multipliziert und zusammengefasst, dass der Parameter t eliminiert wird.
II*: –2y = 6 – 6t
3x – 2y = 21 ⇒ y = 1,5x – 10,5
1
1
2
• „Probe“: Richtungsvektor k = 1,5 3
( ) ()
() ( ) ()
Besonders einfach lässt sich eine parameterfreie Darstellung mithilfe
der Normalvektorform angeben. Der Vektor n
⃑ ist ein Normalvektor
des Richtungsvektors v⃑, P ist ein fixer Punkt der Geraden.
–⃑ – OP
–⃑) = 0 ⇒ n⃑ · OX
–⃑ = n⃑ · OP
–⃑
Es gilt: n⃑ · (OX
X
g
n
P
v
Aus der Normalvektorform kann mithilfe des Skalarprodukts die Gerade unmittelbar in der
Form ax + by = c angegeben werden.
Die Koeffizienten der Geraden entsprechen dabei den Komponenten des Normalvektors, zB:
x
5
·
= 4 ⇒ 5x – 3y = 4
–3 y
( )()
Normalvektorform und parameterfreie Form einer Geraden in der Ebene
a
–⃑ = n
–⃑ ⇒ g: a · x + b · y = c mit n
g: n
⃑ · OX
⃑ · OP
⃑=
b
()
Technologieeinsatz: Geraden in der Ebene
GeoGebra
Eine Gerade kann in Parameterdarstellung oder in Normalvektorform dargestellt werden.
• Bei der Parameterdarstellung definiert
man einen Punkt, zB A=(-3,1) sowie einen
Richtungsvektor, zB a=(2,1). Anschließend
gibt man die Gleichung g:X=A+t*a ein. In
der Algebra-Ansicht wird für den festen
Punkt der Geraden der Schnittpunkt der
Geraden mit der y-Achse angezeigt.
• Zur Darstellung einer Geraden h in
Normalvektorform gibt man die
Gleichung ein, zB: h:3x+4y=15
Je nach Aufgabenstellung kann man nun mit den Geraden weiter verfahren.
Algebra und Geometrie
TE
237
Vektoren
8.105 Gib die Normalvektorform und die parameterfreie Form der Geraden
x
–2
3
g:
=
+t·
an.
y
–5
7
B
() ( ) ()
Lösung:
x
–2
3
–7
=
+t·
⇒ n⃑ =
und P(–2|–5)
y
–5
7
3
() ( ) () ( )
( )() ( )( ) ( )()
B
•
Normalvektor angeben
–7 x
–7 –2
–7 x
·
=
·
⇒ g:
·
= –1
3
y
3
–5
3
y
•
Normalvektorform
g: –7x + 3y = –1
•
Parameterfreie Form
8.106 Gib die Geradengleichung in parameterfreier Form an.
–⃑ = 0 + t · –7
–⃑ = 13 + r · 27
a) g: OX
b) g: OX
13
4
–6
–9
–⃑ = 27 + s · 19
c) g: OX
3
18
8.107 Bestimme die Normalvektorform der Geraden.
–⃑ = 12 + r · –3
–⃑ = –3 + s · 2
a) g: OX
b) g: OX
–7
13
5
–7
–⃑ = –2 + t · 6
c) g: OX
10
4
() ()
B
() ()
B C
C
() ()
() ()
8.109 Ordne den gegebenen Geraden jeweils die idente Gerade zu.
2
() ( )
–⃑ = 1 + t · –2
OX
3
5
2x – 5y = 17
A
B
C
D
238
() ( )
( ) ()
–⃑ = 4 + s · 2
OX
1
–5
5x + 2y = 11
–⃑ = 1 + r · 5
OX
2
–3
3x – y = –11
y
8.110 Eine Gerade g ist durch den Punkt A(–2|–2) und den Vektor
6
3
4
P
bestimmt. Der Punkt P(3|3,5) wird an der Geraden
a⃑ =
nL
2
2
gespiegelt. In der Abbildung ist eine Möglichkeit dargestellt,
P‘
wie die Koordinaten des gespiegelten Punkts P′ ermittelt
2
-2 a 0
4 n 6
R
werden können.
A -2
1) Dokumentiere den Rechenweg zur Ermittlung von P′.
2) Ermittle die Koordinaten des Punkts P′ rechnerisch.
–⃑ den gleichen Winkel mit der Geraden g
3) Zeige, dass die Vektoren –
AP⃑ und AP
′
einschließen.
()
A B
( ) ()
8.108 1) Dokumentiere nachweislich, wie man die Parameterdarstellung einer Geraden
g: ax + by = c ermitteln kann.
2) Gib die Gleichung der Geraden in Parameterdarstellung an.
a) y = 4x – 11
b) 5x – 2y = –10
c) 6x + 8y – 15 = 0
1
B C D
() ()
g
x
n
8.111 Eine Gerade g verläuft durch die Punkte A und B.
1) Gib die Gleichung von g in Parameterdarstellung und in Normalvektorform an.
2) Spiegle den Punkt P an der Geraden und gib die Koordinaten des gespiegelten Punkts
P′ an. Verwende Aufgabe 8.110.
a) A(–3|4), B(5|–2), P(7|9)
b) A(–2|–3), B(8|1), P(6|–8,5)
Algebra und Geometrie
Vektoren
8.9 Geraden und Ebenen im Raum
8.9.1 Geraden im Raum
Geraden im Raum werden wie Geraden in der Ebene mithilfe einer
Parameterdarstellung angegeben. Da es unendlich viele Vektoren gibt,
die auf einen Vektor in ℝ3 normal stehen, gibt es zu jeder Geraden im
Raum unendlich viele andere Geraden, die normal auf diese stehen.
Man kann daher keine Normalvektorform einer Geraden im Raum
angeben.
v
n4
n3
n2
n1
Parameterdarstellung einer Geraden im Raum
–⃑ = OP
–⃑ + t · a⃑ bzw.
g: OX
kurz: g: X = P + t · a⃑
() ( ) ( )
x
y
z
=
xP
yP
zP
+t·
ax
ay
az
mit t∊ℝ
Lagebeziehungen zwischen Geraden im Raum
In der Ebene sind Geraden entweder ident, parallel oder
schneidend. Geraden im Raum können aber auch weder ident
noch parallel sein, noch einen Schnittpunkt haben. Solche
Geraden liegen windschief zueinander.
g1
g3
g2
S
Es soll die Lage der Geraden g und h zueinander untersucht werden.
g:
() ( ) ( ) () ( ) ( )
x
y
z
=
5
–9
8
+t·
3
–1
–4
, h:
x
y
z
=
–1
–2
1
+t·
2
–4
–9
Da die beiden Richtungsvektoren kein Vielfaches voneinander sind, sind sie weder zueinander
parallel noch ident. Zur Untersuchung der Lagebeziehung der beiden Geraden im Raum stellt
man ein lineares Gleichungssystem aus drei Gleichungen auf und berechnet s und t:
I: 5 + 3s = –1 + 2t
• Dieses Gleichungssystem ist überbestimmt. Daher
ermittelt man aus zwei der drei Gleichungen
II: –9 – s = –2 – 4t
eine mögliche Lösung und überprüft anhand der
III: 8 – 4s = 1 – 9t
verbleibenden Gleichung, ob die Werte von s und t
I*: 3s – 2t = –6
⇒ s = –1, t = 1,5 auch die dritte Gleichung erfüllen.
II*: –s + 4t = 7
• Die berechneten Werte für s und t erfüllen diese
?
III: 8 – 4s = 1 – 9t
Gleichung nicht. Das bedeutet, dass die Geraden
III: 8 – 4 · (–1) ≠ 1 – 9 · 1,5
keinen Schnittpunkt haben und daher windschief
III: 12 ≠ –12,5
zueinander liegen.
}
Würden die berechneten Werte auch Gleichung III erfüllen, hätten die Geraden einen
Schnittpunkt. Dessen Koordinaten würde man durch Einsetzen von s bzw. t in eine der
beiden Geradengleichungen erhalten.
8.112 Gib die Gleichung der 1) x-Achse, 2) y-Achse, 3) z-Achse
in Parameterdarstellung an.
A
8.113 Gib die Gleichung der Geraden durch die Punkte A und B in Parameterdarstellung an.
a) g: A(7|1|–3), B(–7|0|–9) b) g: A(–4|10|2), B(3|–4|–8) c) g: A(9|–2|5), B(8|11|–6)
B
8.114 Der Punkt P liegt auf der Geraden durch A und B. Ermittle die fehlenden Koordinaten.
a) g: A(–7|6|11), B(4|3|25); P(4|yA|zA)
b) g: A(15|0,5|–11), B(6|–15,5|7); P(xA|3,5|zA)
B
Algebra und Geometrie
239
Vektoren
8.115 Ermittle, welche Lagebeziehung die Geraden g und h zueinander haben.
B C
g:
() () ( ) () ( ) ( )
x
y
z
4
1
8
=
3
–9
–4
+s·
, h:
x
y
z
=
4
4
27
+t·
–2
7
9
Lösung:
()()
•
Die beiden Geraden sind nicht parallel.
I: 4 + 3s = 4 – 2t
II: 1 – 9s = 4 + 7t
III: 8 – 4s = 27 + 9t
I*: 3s + 2t = 0
⇒ s = 2, t = –3
II*: –9s – 7t = 3
III: 8 – 4 · 2 = 27 + 9 · (–3)
0 = 0 w. A.
•
Aufstellen des Gleichungssystems für g ∩ h.
•
Ermitteln der Parameter s und t aus den
Gleichungen I und II.
Einsetzen von s und t in Gleichung III.
s und t erfüllen Gleichung III, es existiert der
Schnittpunkt der Geraden g und h.
Einsetzen von s in g oder t in h führt auf den
Schnittpunkt S.
3
–9
–4
–2
7
9
}
s in g:
t in h:
•
•
( ) () ( ) ( )
() () ( ) ( )
xs
ys
zs
xs
ys
zs
=
4
1
8
=
4
4
27
+2·
–3·
3
–9
–4
–2
7
9
=
=
10
–17
0
•
10
–17
0
Die Geraden g und h schneiden einander im Punkt S(10|–17|0).
8.116 Ermittle, welche Lagebeziehung die Geraden g1 und g2 zueinander haben.
a) g1: A(9|13|–4), B(–11|13|10); g2: C(4|14|–4), D(13|–13|–10)
b) g1: A(5|–12|8), B(11|–30|0); g2: C(2|–12|9), D(–10|21|24)
B C
A B
D
8.117 Von einer Raumstation in der Umlaufbahn des Planeten
Eldareen E(0|0|0) verlässt eine Fähre zum Zeitpunkt t = 0 s den
Hangar H(0|0|4) und bewegt sich auf geradlinigem Kurs durch
den Weltraum. Zum Zeitpunkt t = 5 s durchläuft sie den
Checkpoint C(3|12|–3). Ein Raumschiff des befreundeten Volks
der Bewchaccas befindet sich zum Startzeitpunkt der Fähre in
B(65|30|–12) und bewegt sich mit der Geschwindigkeit
–15
v = 1,3 E_ geradlinig in Richtung b⃑ = 1
B
s
( )
1
(1 E ⩠ 100 000 km).
1) Stelle die Geradengleichung auf, die den Kurs der Fähre in Abhängigkeit von der Zeit t
beschreibt und berechne die mittlere Geschwindigkeit der Fähre bis C.
2) Stelle die Geradengleichung auf, die den Kurs des Raumschiffs beschreibt. Ermittle,
welchen Punkt sie nach einer Flugzeit von 5 s erreicht.
3) Zeige, dass die beiden Raumfahrzeuge einander nicht begegnen.
A B
8.118 Für ein Experiment zur Untersuchung von Interferenzmustern soll ein Laser A positioniert werden. Vom Punkt
B(0|0|32) geht ein zweiter Laserstrahl aus, der den Strahl von
Laser A im Punkt S(62|59|14) schneiden soll.
( )
–12
Der Strahl aus Laser A soll die Richtung a⃑ = 4 haben
–7
(Angaben in cm).
1) Ermittle, von welchem Punkt der yz-Ebene aus Laser A strahlen muss.
2) Gib eine Formel an, mit der man den Schnittwinkel der Strahlen berechnen kann.
240
Algebra und Geometrie
Vektoren
8.9.2 Ebenen im Raum
Eine Ebene kann in ℝ3 durch drei Punkte A, B und C oder durch einen festen Punkt P(xP|yP|zP)
und zwei Richtungsvektoren a⃑ und b⃑ eindeutig festgelegt werden.
z
1
n b
P
a
1
1
1
OP
O
Da der Normalvektor auf eine Ebene eindeutig bestimmt ist,
kann man eine Ebene auch in Normalvektorform angeben.
X
1
Man erreicht jeden Punkt X(x|y|z) auf der Ebene, indem man
zum Punkt P den Richtungsvektor a⃑ „s-mal“ und den Vektor b⃑
„t-mal“ addiert. Somit kann eine Ebene in Parameterdarstellung
–⃑ = –
OP⃑ + s · a⃑ + t · b⃑
angegeben werden: OX
y
OX
x
Parameterdarstellung einer Ebene im Raum
–⃑ = –
OP⃑ + s · a⃑ + t · b⃑ bzw.
ε: OX
kurz: ε: X = P + s · a⃑ + t · b⃑
() ( ) ( ) ( )
x
y
z
=
xP
yP
zP
ax
ay
az
+s·
+t·
bx
by
bz
Normalvektorform einer Ebene
–⃑ = n · –
OP⃑ ⇒ ε: a · x + b · y + c · z = d mit n⃑ =
ε: n · OX
()
a
b
c
8.119 Gib die Gleichung der Ebene, die durch die Punkte A(1|0|3), B(2|5|−3) und C(−4|2|1)
gegeben ist, 1) in Parameterdarstellung, 2) in Normalvektorform an.
Lösung:
–⃑ =
1) AB
() ()
() ( ) ( )
()()()
( ) ( ) ()
1
5
–6
–⃑ =
ε: OX
2) n⃑ =
2
32
27
1
5
–6
; –
AC⃑ =
1
0
3
+s·
×
–5
2
–2
–⃑ =
· OX
2
32
27
–5
2
–2
•
Zwei Vektoren, die in der gesuchten Ebene
liegen, werden ermittelt.
•
Als fester Punkt kann jeder Punkt der
Ebene verwendet werden, zB A.
2
32
27
•
Der Normalvektor wird mithilfe des
Vektorprodukts ermittelt.
1
0
3
•
Das Skalarprodukt wird berechnet.
1
5
–6
=
·
+t·
–5
2
–2
B
ε: 2x + 32y + 27z = 83
8.120 Gib einen Normalvektor der Ebene ε an.
1) ε: 3x – 5y + 8z = 17
2) ε: −x + z = 3
C
3) ε: y + 2z = 0
8.121 Gib die Gleichung der 1) xy-Ebene, 2) xz-Ebene, 3) yz-Ebene in Parameterdarstellung und in Normalvektorform an.
A
8.122 Auf der Ebene ε liegen die Punkte A, B und C. Gib die Gleichung der Ebene
1) in Parameterdarstellung, 2) in Normalvektorform an.
a) A(3|−5|7), B(4|−3|0), C(11|0|8)
b) A(23|25|17), B(−12|31|25), C(18|0|18)
A
8.123 Zu Dekorationszwecken soll eine dreieckige Platte (siehe Skizze,
Maße in dm), in einer Ecke des Raums angebracht werden. Zur
Befestigung wird noch eine Stange von der Ecke aus, normal auf
die Platte stehend, angebracht. 1 m2 des verwendeten Materials
hat eine Masse von 3,5 kg. Berechne die Länge der Stange und die
Masse der Platte.
A B
Algebra und Geometrie
z
6
1
1 0 1
y
4
3
x
241
Vektoren
8.124 Spiegle den Punkt P(–10|4|4) an einer Ebene ε: x – 2y + z = 10. Dokumentiere zuerst
deinen Lösungsweg und fertige eine Skizze an. Ermittle anschließend P′.
A B C
Lösung:
Zuerst ermittelt man den Normalvektor n⃑ der Ebene ε.
Nun bildet man mit dem Punkt P und dem Normalvektor
die Parameterdarstellung der Geraden g. Schneidet
man die Gerade g mit der Ebene ε, so erhält man
den Durchstoßpunkt S der Geraden mit der Ebene.
–⃑ zum Vektor OS
–⃑
Anschließend addiert man den Vektor PS
und erhält den gespiegelten Punkt P′.
ε: x – 2y + z = 10 ⇒ n⃑ =
g:
() ( ) ( )
x
y
z
–10
4
4
=
+t·
1
–2
1
–⃑ =
PS
=
–10
4
4
+4·
•
1
–2
1
=
–6
–4
8
+
4
–8
4
=
⇒ S(–6|–4|8)
4
–8
4
–⃑ = OS
–⃑ + PS
–⃑ =
OP
′
–6
–4
8
S
P
()
() ( ) ( ) ( )
()
()()( )
x
y
z
g
1
–2
1
g ∩ ε: (–10 + t) – 2 · (4 – 2t) + (4 + t) = 10
t=4
t in g:
P'
Ermitteln des Schnittpunkts
durch Einsetzen von x, y und
z aus der Geraden g in die
Normalvektorform der Ebene
und lösen der Gleichung nach t.
–2
–12
12
Der gespiegelte Punkt hat die Koordinaten P′(–2|–12|12).
8.125 Spiegle den Punkt P an der Ebene ε.
a) ε: –3x + y + 2z = 2, P(1|–4|8)
b) ε: –4x – 7y + 2z = –12, P(–7|12|7)
A B
D
8.126 Zwei Ebenen ε1 und ε2 sind in Normalvektorform gegeben.
1) Erkläre anhand der nebenstehenden Abbildung, wie
man den Scheitelwinkel φ zwischen den Ebenen ε1 und
ε2 berechnen kann.
2) Gib eine Formel zur Berechnung des Schnittwinkels φ
zwischen zwei Ebenen ε1 und ε2 an.
n1 ‘
n2
1
A B
D
1
A
c) ε: 4,5x + 2,8y + 5,3z = –25, P(–11,5|–5,4|–23,9)
d) ε: 3x + 8y = 29, P(0|31|4)
2
1
8.127 Gegeben sind die Geraden g und h:
g:
() ( ) ( ) () () ()
x
y
z
=
–1
5
–10
+s·
2
–3
6
, h:
x
y
z
=
3
5
5
+t·
0
2
1
1) Zeige nachweislich, dass die Geraden g und h einander im Punkt A(3|–1|2) schneiden.
2) Ermittle die parameterfreie Gleichung der Ebene ε, die von den Geraden g und h
aufgespannt wird.
3) Überprüfe, ob die Punkte B(5|–4|8) und C(3|1|3) auf der Ebene ε liegen.
–⃑ und AC
–⃑ normal aufeinander stehen.
4) Zeige nachweislich, dass die Vektoren AB
5) Die Punkte A, B und C sind Eckpunkte der Basisfläche einer geraden rechteckigen
Pyramide mit der Höhe h = 7 · √––
5 E. Ermittle die Koordinaten des Eckpunkts D sowie
die der Spitze S der Pyramide. Gib beide Lösungen für die Spitze an.
242
Algebra und Geometrie
Vektoren
Zusammenfassung
()
( )
( )
ax
–ay
a
im ℝ2: n–⃑L =
... nach links n–⃑R = y ... nach rechts
ay
ax
–ax
Normalvektor von a⃑ =
Skalarprodukt: a⃑ · b⃑ = | a⃑ | · | b⃑ | · cos(φ)
a
b
im ℝ2: a⃑ · b⃑ = x · x = ax · bx + ay · by
ay by
im ℝ3: a⃑ · b⃑ =
a⃑ ⊥ b⃑ ⇔ a⃑ · b⃑ = 0 (a⃑, b⃑ ≠ o⃑ )
( )( )
()()
ax
ay
az
·
bx
by
bz
= ax · bx + ay · by + az · bz
⃑
| a⃑ | · | b |
a⃑ · b
Winkel zwischen zwei Vektoren a⃑ und b⃑ : cos(φ) = _____
⃑
Vektorprodukt im ℝ3: |a⃑ × b⃑| = | a⃑ | · | b⃑ | · sin(φ), 0° < φ < 180° bzw. a⃑ × b⃑ =
Flächeninhalt eines von den Vektoren a⃑ und b⃑ aufgespannten ...
Parallelogramms: AP = √––––––––––––
a⃑2 · b⃑2 – (a⃑ · b⃑)2 = |axby – aybx|
Volumenberechnung:
Parallelepiped: V = |(a⃑ × b⃑) · c⃑|
(
ay · bz – az · by
az · bx – ax · bz
ax · by – ay · bx
)
Dreiecks: AD = _12 · AP
Tetraeder: V = 1_6 · |(a⃑ × b⃑) · c⃑|
Geradengleichung
–⃑ = OP
–⃑ + t · a⃑ mit t∊ℝ
im ℝ2 und im ℝ3: Parameterdarstellung ... g: OX
a
–⃑ = n⃑ · OP
–⃑ bzw. g: ax + by = c mit n
im ℝ2:
Normalvektorform ... g: n
⃑ · OX
⃑=
b
Ebenengleichung im ℝ3
–⃑ = OP
–⃑ + s · a⃑ + t · b⃑ mit s, t∊ℝ
Parameterdarstellung ... ε: OX
a
–⃑ = n
–⃑ bzw. ε: ax + by + cz = d mit n
Normalvektorform ... ε: n⃑ · OX
⃑ · OP
⃑= b
()
()
c
Weitere Aufgaben
Aufgaben 8.128 − 8.129: Berechne jeweils das Skalarprodukt der beiden Vektoren und den
Winkel, den sie miteinander einschließen.
7
12 ⃑ 14
7
2 ⃑
3
8.128 a) a⃑ = , b⃑ =
b) a⃑ =
,b=
c) a⃑ =
,b=
8
–5
–3
–3
–3
–1
8.129 a) a⃑ =
() ( )
() ()
4
6
–2
, b⃑ =
1
–7
5
b) a⃑ =
() ()
() ()
1
4
–1
, b⃑ =
–4
7
3
c) a⃑ =
() ()
() ( )
3
5
1
, b⃑ =
–9
–6
6
–⃑ × CD
–⃑.
8.130 Berechne das Vektorprodukt AB
a) A(–3|9|5), B(3|2|8), C(1|1|–4), D(–1|8|4) b) A(3|4|4), B(12|–1|–3), C(2|7|2), D(9|4|5)
8.131 Kreuze die wahre Ausage an.
B
B
B
C
Das Vektorprodukt ist ein Skalar.
Das Skalarprodukt ist nicht kommutativ.
Hat das Vektorprodukt den Wert 0, stehen die Vektoren normal aufeinander.
Die Maßzahl des Skalarprodukts zweier Vektoren ist gleich dem Flächeninhalt
eines von ihnen aufgespannten Dreiecks.
Das Ergebnis des Vektorprodukts ist ein Vektor, der auf beide Vektoren normal
steht.
Algebra und Geometrie
243
Vektoren
A B
D
8.132 Die so genannte „Lange Zählung“ des Jahrtausende lang währenden Kalenders der Mayas
vollendete am 21. 12. 2012 einen Zyklus, das 13. Baktun. Dies rief einige Weltuntergangsprophezeihungen hervor. Es wurde auch gemunkelt, dass an diesem Tag die Planeten in
y
einer Linie angeordnet seien, was allerdings widerlegt
werden konnte. Die Grafik zeigt näherungsweise die
Mars
1
Konstellation der inneren Planeten am 21. 12. 2012
um 00:00 Uhr. Dabei wurde angenommen, dass die
x
Erde
Sonne
Planetenbahnen auf einer Ebene kreisförmig um die Sonne
0
1
-1
verlaufen (Angaben in Astronomischen Einheiten AE).
Merkur
Sonne: S(0|0)
Mars: M(1,07|1,07)
Venus
-1
Erde: E(–1|0)
Venus: V(0,27|–0,67)
1) Berechne die Entfernungen der Planeten Mars und
Venus von der Sonne am 21. 12. 2012 um 0:00 Uhr.
1,19
2) Der Richtungsvektor von der Erde zum Merkur war zu dieser Zeit e⃑ =
. Die
–0,33
Planeten waren 1,23 AE voneinander entfernt. Ermittle die Koordinaten des Merkur.
3) Zeige, dass Erde, Sonne und Mars an diesem Tag einen Winkel von rund 135°
eingeschlossen haben.
4) Gib an, zu welchem Planeten man gelangt wäre, wenn man vom Mars ausgehend die
–2,51 ⃑
0,82
1,87
–0,98
,b=
, c⃑ =
und d⃑ =
eingeschlagen hätte.
Wege a⃑ =
–0,60
–1,40
0,77
–0,51
5) Argumentiere, ob eine Änderung der Reihenfolge beim „Abgehen“ der Vektoren in
Aufgabe 4) zu einem anderen Ergebnis führt.
( )
( ) ( ) ( )
( )
B
8.133 Berechne die gesuchten Größen im angegebenen Parallelogramm ABCD.
1) fehlende Punktkoordinaten 2) Umfang 3) Höhen 4) Flächeninhalt
a) A(5|–4), B(7|–), C, D(–5|–3)
b) A(6|–3|9), B(–1|7|–2), C(2|–4|3), D
B
8.134 Berechne das Volumen des Parallelepipeds mit den gegebenen Eckpunkten.
a) A(1|13|7), B(5|6|4), C(15|3|–4), E(12|9|8) b) F(1|2|7), G(3|1|–2), H(–1|3|–6), C(3|0|1)
kg
8.135 Ein optischer Körper aus Flintglas (Dichte ρ = 3,6 ___ ) hat die Form
B
D
F
dm3
eines Tetraeders. Die Basisfläche ist durch die Punkte A(–2|3|1),
B(2|–1|3) und C(6|–3|1) gegeben (Angaben in cm). Die Höhe geht
durch den Schwerpunkt der Basisfläche. Der Tetraeder ist 12 cm
hoch.
1) Zeige, dass die Basisfläche ein gleichschenkliges Dreieck ist.
2) Ermittle die Koordinaten des Schwerpunkts S der Basisfläche
und der Spitze D. Gib beide Lösungen für D an.
3) Berechne das Volumen und die Masse des optischen Körpers.
244
A
D
A
D
8.136 Gib drei verschiedene Bedingungen für zwei Vektoren a⃑ und b⃑ an, sodass a⃑ × b⃑ = o⃑ gilt,
und begründe deine Antwort.
8.137 Gegeben ist das Quadrat ABCD. Verbindet man die
Seitenmittelpunkte E, F, G und H mit den gegenüberliegenden
Eckpunkten, so entsteht das rot eingezeichnete Achteck. Zeige
mithilfe der Vektorrechnung, dass es sich nicht um ein
regelmäßiges Achteck handelt.
Hinweis: Ein n-Eck heißt regelmäßig, wenn alle Seiten gleich lang
und alle Innenwinkel gleich groß sind.
Algebra und Geometrie
y
D (0 2)
G
C (2 2)
F
H
x
A (0 0)
E
B (2 0)
Vektoren
Anwendungen aus den Naturwissenschaften
8.138 Zwei Kräfte F–⃑1 und F–⃑2 greifen im selben Punkt an. Ermittle Richtung und Betrag der
resultierenden Kraft F–⃑ sowie die Winkel, die F–⃑ und F–⃑ einschließen (Kräfte in N).
R
() ()
6
8
a) F–⃑1 = , F–⃑2 =
4
1
1
b) F–⃑1 =
A B
2
() ()
, F–⃑2 =
52
34
26
12
48
96
8.139 Von Frederikshavn in Dänemark kann man die Stadt Göteborg in Schweden auf
annähernd geradlinigem Weg über das Kattegat, einem östlichen Teil der Nordsee, mit
einer Fähre erreichen. Wird Frederikshavn in den Ursprung eines Koordinatensystems
F(0|0) gelegt, so liegt Göteborg im Punkt G(81|26) (Angaben in km). Im Kattegat
herrscht eine nördliche Meeresströmung mit einer
Geschwindigkeit von vS = 0,54 kn (Knoten).
angesteuerter
Kurs
Ein Reeder gibt an, dass die Überfahrt auf
vE
direktem Weg erfolgt und 3,5 Stunden dauert.
Göteborg
vR
vS
Dafür muss seine Fähre einen Kurs ansteuern,
der im Winkel α zur Strecke FG liegt. Auf diesem
v
vE
Frederikshavn S
Kurs fährt sie mit der Eigengeschwindigkeit vE.
__
Hinweis: 1 kn = 1,852 km
h
1) Ermittle den Vektor der resultierenden Geschwindigkeit –v⃑,
R die notwendig ist, um
Göteborg in der vorgegebenen Zeit auf der direktem Weg zu erreichen.
2) Ermittle den Vektor und den Betrag der Eigengeschwindigkeit v–⃑E der Fähre.
3) Welchen Winkel α schließt der angesteuerte Kurs mit dem direkten Weg ein?
8.140 Auf einen Massepunkt P(2|3|0) wirkt eine Kraft F⃑ =
()
10
3
5
. Ermittle die Richtung und
A B
A B
den Betrag des Drehmoments bezüglich des Ursprungs (Längen in m, Kräfte in N).
8.141 Auf einen Massenpunkt in R(rx|ry|rz) wirkt ein Impuls p
⃑=
()
0
py
pz
. Wie lauten die
A B
D
A B
D
Koordinaten des Punkts R, wenn der Drehimpuls L⃑ = 0⃑ ist?
Begründe deine Antwort durch eine Skizze und mithilfe des Vektorprodukts.
8.142 An einem regelmäßigen Dreibein mit der Höhe h = 2 m soll
eine Last montiert werden. Die Grundfläche ist ein
gleichseitiges Dreieck mit der Seitenlänge a = 2 m. Jedes Bein
kann eine Kraft von maximal 200 N aufnehmen.
1) Begründe, warum die Last direkt über dem Schwerpunkt
des gleichseitigen Dreiecks liegt.
2) Ermittle, wie groß die Last auf dem Dreibein höchstens
sein kann.
z
F
FG
h
a
x
O
a
F
F
a
y
Parameterdarstellung und Normalvektorform von Geraden und Ebenen
8.143 Gib die Gleichung der Geraden durch die gegebenen Punkte in allen in diesem Abschnitt
behandelten möglichen Darstellungsformen an.
a) A(6|–2), B(3|0)
c) K(–9|4), L(5|6)
e) R(15|–11), S(–23|19)
b) C(1|4|–3), D(–2|5|2)
d) M(–5|2|4), N(3|4|–1)
f) T(12|–9|8), U(4|–27|–3)
B
8.144 Gib die Gleichung der Ebene durch die gegebenen Punkte in Parameterdarstellung und in
Normalvektorform an.
a) A(–3|4|0), B(2|–1|5), C(4|3|–6)
b) P(10|–7|–2), Q(8|–3|1), R(5|–4|–3)
B
Algebra und Geometrie
245
Vektoren
B
8.145 Berechne die Koordinaten des Schnittpunkts der Geraden g1 und g2.
a) g1: A(3|–1), B(–4|2); g2: C(–4|6), D(0|–4) b) g1: A(5|3), B(–2|–2); g2: C(–4|5), D(0|–7)
B C
8.146 Ermittle die gegenseitige Lage der Geraden g1 und g2.
a) g1: y =
( ) ()
9
–13
–4
+t·
5
3
–4
, g2: y =
() () ( ) () () ()
() ( )
( ) ()
4
14
28
+s·
1
–3
2
b) g1: y =
5
–12
8
+t·
3
–9
–4
8
12
1
, g2: y =
+s·
–2
7
9
–⃑ = 3 + u · 2 und h: OX
–⃑ = 4 + v · 5 .
8.147 Gegeben sind die Geraden g: OX
7
–3
–11
–5
1) Berechne die Koordinaten des Schnittpunkts S der beiden Geraden.
2) Gib die Normalvektorform der Geraden g an.
3) Gib die Parameterdarstellung einer Geraden an, die normal auf h steht und durch den
Punkt Q(1|2) verläuft.
A B
8.148 Von einer Raute kennt man die Eckpunkte A(4|5|0) und C(2|1|4). Der Punkt B liegt auf
0
–⃑ = –1
1 +s· 1 .
der Geraden g: OX
A B
( ) ()
–2
0
1) Ermittle die Koordinaten der fehlenden Eckpunkte und des Mittelpunkts.
2) Berechne den Umfang und den Flächeninhalt der Raute.
8.149 Beim Poolbillard müssen verschiedenfärbige Kugeln durch Anspielen
einer weißen Kugel mit einem Spielstock, dem Queue [sprich: „Köh“]
in 6 Taschen versenkt werden, die gleichmäßig am Bandenspiegel des
ebenen rechteckigen Spielfelds verteilt sind (siehe Abbildung). Das
Spielfeld hat die Abmessungen 2,24 m x 1,12 m.
1) Gib die Punktkoordinaten der Taschen an. Wähle die linke untere
Ecke als Ursprung des Koordinatensystems.
2) Anna und Rolf spielen eine Partie Poolbillard. Am Ende ist noch eine blaue Kugel an
der Position B(0,2|1,8) übrig. Die weiße Kugel befindet sich an der Position W(1,0|0,3).
Rolf spielt mit der weißen Kugel die blaue Kugel direkt an. Berechne, ob die blaue
Kugel dadurch in der linken oberen Ecke versenkt wird (Angaben in m).
3) Rolf verfehlt die blaue Kugel und begeht damit ein Foul. Nun darf Anna für ihren Stoß
die weiße Kugel auf einen beliebigen Punkt des Spielfelds legen. Sie möchte angeben
und entscheidet sich deshalb dazu, die blaue Kugel über den Bandenspiegel so ohne
Schnitt mit der weißen Kugel anzuspielen, dass sie direkt in die rechte obere Ecke rollt.
Ermittle die Gleichung jener Geraden, auf der sie die weiße Kugel positionieren kann,
in Normalvektorform. Gib einen sinnvollen Definitionsbereich an.
Hinweis: Einfallswinkel = Reflexionswinkel
Bandenspiegel
A B C
A B
A B
D
8.150 Gegeben sind die Punkte A(1|2|3), B(3|yB|5) und D(2|4|1).
–⃑ normal steht.
1) Berechne die fehlende Koordinate von B so, dass –
AB⃑ auf AD
2) Ergänze die Punkte zu einem Rechteck ABCD und zeige, dass dieses Rechteck ein
Quadrat ist.
3) Das Quadrat ist die Grundfläche einer quadratischen Pyramide ABCDS, deren Höhe
das √––
2 -fache der Quadratdiagonale ist. Ermittle beide Lösungen für die Spitze S.
8.151 Eine gerade, rechteckige Pyramide hat die Eckpunkte A(–2|1|4) und D(–4|–7|2) sowie die
2
–⃑ = 14 + s · –1
.
Spitze S(–3|6|3). Die Höhe liegt auf der Geraden h: OX
() ( )
7
2
1) Fertige eine Skizze an.
2) Berechne die fehlenden Eckpunkte, das Volumen der Pyramide sowie den Winkel, den
die Höhe mit einer der Seitenkanten einschließt.
246
Algebra und Geometrie
Vektoren
Wissens-Check
gelöst
1
Ich kann den Vektor zwischen zwei Punkten angeben, zB A(4|–5), B(–3|7).
–⃑ =
AB
2
8
Berechne | a⃑ |, a–⃑0 und n–⃑L für a⃑ = .
6
3
4
()
Ich kann das Skalarprodukt erklären und auf zwei Arten berechnen.
–⃑ und AC
–⃑:
Berechne den Winkel zwischen den Vektoren AB
A(3|5|1), B(2|−1|3), C(−1|−2|8)
Berechne die fehlende Koordinate, sodass die beiden Vektoren orthogonal
() ()
3
–4
az
–1
1
4
5
sind: a⃑ =
6
Welche der Behauptungen ist richtig? Begründe deine Antwort.
B) a⃑ × b⃑ = –b⃑ × a⃑
A) a⃑ × b⃑ = b⃑ × a⃑
7
Ich kann physikalische Anwendungen des Vektorprodukts angeben.
8
–⃑ = –1 + t · 3 in Normalvektorform an.
Gib die Gerade OX
4
–5
9
Ich kann die gegenseitige Lage von Geraden in der Ebene anhand der
Parameterdarstellung erkennen.
, b⃑ =
() ()
Ermittle die Parameterdarstellungen der
Geraden g und h aus der nebenstehenden
Zeichnung.
y
6
h
5
4
3
10
2
1
x
-3 -2
-1 0
-1
1
2
3
4
5
6
7
g
-2
11
Gib die Parameterdarstellung und die Normalvektorform der Ebene durch
die Punkte A(0|3|−1), B(−2|4|0) und C(1|0|1) an.
12
Ich kann begründen, warum es keine Normalvektorform einer Geraden im
Raum gibt.
Lösung:
0,8 –
–6
–⃑ = –7
2) | a⃑ | = 10; a–⃑0 =
; n⃑ =
3) siehe Seiten 214ff.
4) φ ≈ 28,6°
5) az = 47_
1) AB
12
0,6 L
8
6) B
7) ZB: Drehmoment, Drehimpuls, Lorentzkraft
8) 5x + 3y = 7
9) siehe Seite 235
1
–⃑ = –2 + s · 5 , h: OX
–⃑ = 2 + t · 1
–⃑ = 30 + s · –2
1 + t · –3 ; x + y + z = 2
11) OX
10) ZB: g: OX
3
–2
2
2
1
–1
2
12) siehe Seite 239
( ) ( )
( )
() ()
() () ()
( ) ( )
Algebra und Geometrie
247