Lernzirkel Kreis
Werbung

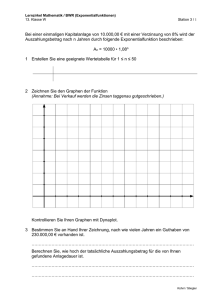
DOWNLOAD Albrecht Schiekofer Lernzirkel Kreis Downloadauszug aus dem Originaltitel: ������ Albrecht Schiekofer: Lernzirkel Ebene Geometrie Albrecht Schiekofer: Lernzirkel Kreis Persen Verlag GmbH, Buxtehude © Persen Verlag GmbH, Buxtehude 0 –4 –3 –2 –1 1 2 3 2 3 4 x S � a „Winkelwissen“ Optische Täuschungen 10 1 spezielle Winkelpaare Parallelen konstruieren 9 –1 Winkel an der Windrose (Himmelsrichtungen) Senkrechte konstruieren 8 –2 Winkel an der Windrose (Winkel bestimmen) senkrecht oder parallel 7 –3 Winkel an der Uhr Linien (Fachbegriffe) 6 –4 Winkel zeichnen Symmetrieachsen bestimmen 5 b Winkel messen Spiegelpunkte bestimmen 4 4 Winkel mit Punktefolge bestimmen Koordinaten eintragen 3 y rechtwinkliges Dreieck griechische Buchstaben Koordinaten bestimmen 2 A � b c � C a � B Dreieckskonstruktion Winkelberechnung Spiegelung von Dreiecken Winkelberechnung Pythagoras Flächenberechnung Eigenschaften von Dreiecken Winkelberechnung am Dreieck Dreiecksarten Winkelarten Koordinatensystem (Fachbegriffe) 1 Lernzirkel C Dreieck Lernzirkel B Winkel Lernzirkel A Grundlagen der Geometrie A d a D B c b Die Menge der Vierecke C Viereckskonstruktion 4 3 2 1 4 3 2 1 0 1 2 3 4 1 2 3 4 Kreiskonstruktion Berechnungen am Kreis (Kreisbogen, Kreismittelpunkt, Kreisausschnitt) Kreisflächen berechnen Durchmesser bestimmen Vierecke bestimmen (Winkel) Winkelsumme im Viereck Radius/Fläche berechnen Radius/Umfang berechnen Umkreise Kreise im Koordinatensystem Kreise zeichnen Begriffe am Kreis Lernzirkel E Kreis Umfang von Vierecken berechnen Flächenberechnung Vierecke zeichnen Steckbriefe Vierecke Vierecke bestimmen (Koordinatensystem) Kennzeichnung von Vierecken Lernzirkel D Viereck Lernzirkel: inhaltlicher Aufbau 11 4 Station 1 – Aufgabe 3 2 1 4 3 2 1 Benenne die Begriffe am Kreis richtig. 0 1 2 3 4 1 2 3 4 1 2 3 4 k a) k V d M B A b) r V c) d V Lernzirkel E – Kreis r d) M V e) AB V 4 Station 1 – Lösung 3 2 1 4 3 2 1 0 1 2 3 4 k a) k V Kreislinie d M B A b) r V Radius c) d V Durchmesser d) M V Mittelpunkt e) AB V Sehne Lernzirkel E – Kreis r Für jeden richtig benannten Begriff gibt es 1 Punkt. ������ Albrecht Schiekofer: Lernzirkel EbeneKreis Geometrie Albrecht Schiekofer: Lernzirkel Persen Verlag GmbH, © Persen Verlag Buxtehude GmbH, Buxtehude 55 2 4 Station 2 – Aufgabe 3 2 1 4 3 2 1 Zeichne zwei Kreise mit r1 = 1,5 cm und r2 = 2 cm, die 0 1 2 3 4 1 2 3 4 1 2 3 4 a) einen gemeinsamen Mittelpunkt haben. b) sich in zwei Punkten schneiden. Lernzirkel E – Kreis c) sich in einem Punkt schneiden. d) so liegen, dass der kleinere Kreis durch den Mittelpunkt des größeren Kreises verläuft. e) keinen gemeinsamen Punkt haben. 4 Station 2 – Lösung 3 2 1 4 3 2 1 0 1 2 3 a) b) c) B1 A C1 C2 e) D1 D2 E1 E2 oder E3 E4 Lernzirkel E – Kreis d) B2 4 Für jedes richtig gezeichnete Kreispaar gibt es 1 Punkt. (Lösungen nicht maßstabsgetreu.) ������ Albrecht Schiekofer: Lernzirkel EbeneKreis Geometrie Albrecht Schiekofer: Lernzirkel Persen Verlag GmbH, © Persen Verlag Buxtehude GmbH, Buxtehude 56 3 4 Station 3 – Aufgabe 3 2 1 4 3 2 1 Zeichne folgende Kreise: k1 r = 1,5 cm um A (2,5/1,5), k2 r = 2,3 cm um B (6/3,5) und k3 r = 2,5 cm um C (7/8) als Mittelpunkt. In welchen Punkten schneiden diese die Gerade g? 0 1 2 3 4 1 2 3 4 1 2 3 4 11 10 Lernzirkel E – Kreis 9 8 7 6 5 4 3 2 1 –2 –1 1 2 3 4 5 6 7 8 9 10 4 Station 3 – Lösung 3 2 1 4 3 2 1 0 1 2 3 11 4 10 C2 9 C A1 (1/1,5) 8 A2 (2,5/3) C1 6 B1 B1 (4,5/5) 5 4 B C1 (5,5/6) A2 3 2 C2 (9/9,5) A1 A 1 –2 –1 1 2 3 4 5 6 7 8 9 Lernzirkel E – Kreis 7 10 –1 Für jeden richtigen Schnittpunkt gibt es 1 Punkt. (Lösung nicht maßstabsgetreu) ������ Albrecht Schiekofer: Lernzirkel EbeneKreis Geometrie Albrecht Schiekofer: Lernzirkel Persen Verlag GmbH, © Persen Verlag Buxtehude GmbH, Buxtehude 57 4 4 Station 4 – Aufgabe 3 2 1 4 3 2 1 Radio „Donauwelle“ in Ingolstadt erweitert den Umkreis seiner Reichweite von 30 km auf 60 km. Können folgende Orte nun die „Donauwelle“ empfangen? 0 1 2 3 4 1 2 3 4 1 2 3 4 Augsburg Lernzirkel E – Kreis Ulm Regensburg Nürnberg Donauwörth 0,35 cm ^ = 10 km 4 Station 4 – Lösung 3 2 1 4 3 2 1 0 1 2 3 4 Augsburg x Ulm Regensburg x x Nürnberg Donauwörth nein x x Lernzirkel E – Kreis ja Für jede richtige Lösung gibt es 1 Punkt. ������ Albrecht Schiekofer: Lernzirkel EbeneKreis Geometrie Albrecht Schiekofer: Lernzirkel Persen Verlag GmbH, © Persen Verlag Buxtehude GmbH, Buxtehude 58 5 4 Station 5 – Aufgabe 3 2 1 4 3 2 1 Berechne jeweils die fehlenden Werte (Radius und Umfang). Runde jeweils auf 1 Dezimalstelle. (Rechne mit / = 3,14.) r b) 2,1 cm U c) d) 14,9 dm 7,9 m 60,8 mm 1 2 3 4 1 2 3 4 1 2 3 4 Lernzirkel E – Kreis a) 0 e) 127,3 km 4 Station 5 – Lösung 3 2 1 4 3 2 1 0 1 2 3 4 b) c) d) e) r 2,1 cm 9,7 mm 14,9 dm 7,9 m 20,3 km U 13,2 cm 60,8 mm 93,6 dm 49,6 m 127,3 km Lernzirkel E – Kreis a) Für jeden richtig berechneten Wert gibt es 1 Punkt. ������ Albrecht Schiekofer: Lernzirkel EbeneKreis Geometrie Albrecht Schiekofer: Lernzirkel Persen Verlag GmbH, © Persen Verlag Buxtehude GmbH, Buxtehude 59 6 4 Station 6 – Aufgabe 3 2 1 4 3 2 1 Berechne jeweils die fehlenden Werte (Radius und Fläche). Runde jeweils auf 1 Dezimalstelle. (Rechne mit / = 3,14.) r b) 1,9 cm c) 27,4 m 563,8 km2 A d) 1 2 3 4 1 2 3 4 1 2 3 4 Lernzirkel E – Kreis a) 0 e) 32,4 dm 215,3 mm2 4 Station 6 – Lösung 3 2 1 4 3 2 1 0 1 2 3 4 b) c) d) e) r 1,9 cm 13,4 km 27,4 m 8,3 mm 32,4 dm A 11,3 cm2 563,8 km2 2 357,4 m2 215,3 mm2 3 296,2 dm2 Lernzirkel E – Kreis a) Für jeden richtig berechneten Wert gibt es 1 Punkt. ������ Albrecht Schiekofer: Lernzirkel EbeneKreis Geometrie Albrecht Schiekofer: Lernzirkel Persen Verlag GmbH, © Persen Verlag Buxtehude GmbH, Buxtehude 60 7 4 Station 7 – Aufgabe 3 2 1 4 3 2 1 Bestimme in mm den Durchmesser der Euromünzen. (Du darfst auch die jeweiligen Originalmünzen dazu verwenden.) a) b) 1 2 3 4 1 2 3 4 1 2 3 4 c) Lernzirkel E – Kreis d) 0 e) 4 Station 7 – Lösung 3 2 1 4 3 2 1 0 1 Abweichungen � 1 mm sind erlaubt. 2 3 4 a) b) 24,25 mm d) 23,25 mm e) 16,25 mm Lernzirkel E – Kreis 25,75 mm c) 22,25 mm Für jeden richtig gemessenen Durchmesser gibt es 1 Punkt. ������ Albrecht Schiekofer: Lernzirkel EbeneKreis Geometrie Albrecht Schiekofer: Lernzirkel Persen Verlag GmbH, © Persen Verlag Buxtehude GmbH, Buxtehude 61 8 4 Station 8 – Aufgabe 3 2 1 4 3 2 1 Berechne jeweils die grau gefärbte Fläche. Die Seitenlänge der Quadrate ist jeweils 4 cm groß. Runde immer auf 2 Dezimalstellen. (Rechne mit / = 3,14.) a) b) 1 2 3 4 1 2 3 4 1 2 3 4 c) Lernzirkel E – Kreis 2 cm d) 0 2 cm e) 1 cm 1 cm 1 cm 4 Station 8 – Lösung 3 2 1 4 3 2 1 0 1 2 3 4 a) b) 9,72 cm2 d) 3,44 cm2 e) 11,78 cm2 6,58 cm2 Lernzirkel E – Kreis 3,44 cm2 c) Für jede richtig berechnete Fläche gibt es 1 Punkt. ������ Albrecht Schiekofer: Lernzirkel EbeneKreis Geometrie Albrecht Schiekofer: Lernzirkel Persen Verlag GmbH, © Persen Verlag Buxtehude GmbH, Buxtehude 62 9 4 Station 9 – Aufgabe 3 2 1 4 3 2 1 Ein Kreisring mit einem äußeren Durchmesser von 9 cm und einem inneren von 2 cm wird in sechs gleich große Teile geteilt. Fertige eine Planskizze. (Rechne mit / = 3,14.) 0 1 2 3 4 1 2 3 4 1 2 3 4 a) Wie groß ist der Mittelpunktswinkel eines Kreisausschnittes? Lernzirkel E – Kreis b) Wie groß ist der äußere Kreisbogen eines Kreisausschnittes? c) Wie groß ist der innere Kreisbogen eines Kreisausschnittes? d) Wie groß ist die Fläche des Kreisausschnittes? (Runde das Endergebnis auf zwei Dezimalstellen.) e) Wie groß ist der Umfang des gesamten Kreisringes? 4 Station 9 – Lösung 3 2 1 4 3 2 1 0 1 2 3 4 a) 60 ° c) 1,05 cm d) 10,07 cm2 e) 28,26 cm Lernzirkel E – Kreis b) 4,71 cm Für jedes richtige Ergebnis gibt es 1 Punkt. ������ Albrecht Schiekofer: Lernzirkel EbeneKreis Geometrie Albrecht Schiekofer: Lernzirkel Persen Verlag GmbH, © Persen Verlag Buxtehude GmbH, Buxtehude 63 10 4 Station 10 – Aufgabe 3 2 1 4 3 2 1 Von einer achtblättrigen Blume sind nur noch drei Blütenblätter (X,Y,Z) übrig. Ordne die fehlenden Blütenblätter (A – E) genauso an wie die ersten drei. An welchen Stellen sind die Blütenblätter mit dem Blütenboden verbunden? 0 1 2 3 4 1 2 3 4 1 2 3 4 11 10 Lernzirkel E – Kreis Y 9 X Z 8 7 M 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 10 11 4 Station 10 – Lösung 3 2 1 4 3 2 1 0 1 2 3 4 11 10 Y 9 X A (7,6/5,5) Z 8 M 6 C (5,5/3,4) A E 5 B D 4 D (4/4) C 3 E (3,4/5,5) 2 1 0 1 2 3 4 5 6 7 8 9 10 Lernzirkel E – Kreis B (7/4) 7 11 Für jeden richtig benannten Berührungspunkt (Blütenblatt – Blütenboden) gibt es 1 Punkt. ������ Albrecht Schiekofer: Lernzirkel EbeneKreis Geometrie Albrecht Schiekofer: Lernzirkel Persen Verlag GmbH, © Persen Verlag Buxtehude GmbH, Buxtehude 64 11 4 Arbeitsblatt 1 3 2 1 4 3 2 1 0 1 2 Station 1: 3 4 a) k V ________________________________________ b) r V ________________________________________ c) d V ________________________________________ d) M V ________________________________________ e) AB V ________________________________________ Punkte: ______ Station 2: a) b) c) d) B2 C1 C2 e) D1 D2 E1 E2 oder E3 E4 Lernzirkel E – Kreis B1 A Punkte: ______ Station 3: A1 ( / ) A2 ( / ) C1 ( / ) C2 ( / ) B1 ( / ) Punkte: ______ ������ Albrecht Schiekofer: Lernzirkel EbeneKreis Geometrie Albrecht Schiekofer: Lernzirkel Persen Verlag GmbH, © Persen Verlag Buxtehude GmbH, Buxtehude 65 12 1 2 3 4 4 Arbeitsblatt 2 3 2 1 4 3 2 1 0 1 2 Station 4: 3 4 ja nein Augsburg Ulm Regensburg Nürnberg Donauwörth Punkte: ______ Station 6: a) __________________________________ a) _________________________________ b) __________________________________ b) _________________________________ c) __________________________________ c) _________________________________ d) __________________________________ d) _________________________________ e) __________________________________ e) _________________________________ Punkte: ______ Lernzirkel E – Kreis Station 5: Punkte: ______ Station 7: a) ___________ mm b) ___________ mm d) ___________ mm e) ___________ mm ������ Albrecht Schiekofer: Lernzirkel EbeneKreis Geometrie Albrecht Schiekofer: Lernzirkel Persen Verlag GmbH, © Persen Verlag Buxtehude GmbH, Buxtehude c) ___________ mm Punkte: ______ 66 13 1 2 3 4 4 Arbeitsblatt 3 3 2 1 4 3 2 1 0 1 2 Station 8: Station 9: 3 4 a) __________________________________ a) _________________________________ b) __________________________________ b) _________________________________ c) __________________________________ c) _________________________________ d) __________________________________ d) _________________________________ e) __________________________________ e) _________________________________ Punkte: ______ Punkte: ______ Station 10: 11 Lernzirkel E – Kreis 10 Y 9 X Z 8 7 M 6 5 4 3 2 1 0 1 2 3 4 5 6 7 A( / ) B( / ) D( / ) E( / ) 8 C( 9 10 / 11 ) Punkte: ______ Gesamtpunkte: ______ ������ Albrecht Schiekofer: Lernzirkel EbeneKreis Geometrie Albrecht Schiekofer: Lernzirkel Persen Verlag GmbH, © Persen Verlag Buxtehude GmbH, Buxtehude 67 14 1 2 3 4 Anleitung (1) Die Lernzirkel Mathematik „Ebene Geometrie“ werden von der Schüleraktivität beherrscht. Der Lehrer ist Organisator: Er leitet an, unterstützt und hat Zeit, um individuell auf einzelne Schülerinnen und Schüler einzugehen. Der Lernzirkel bedarf bis auf die Vorbereitung der Stationen für die Lehrkraft relativ wenig Zeitaufwand, außerdem ist er so organisiert, dass jeweils 2-3 Schülerinnen und Schüler (je nach Klassenstärke) im Klassenzimmer von Station zu Station wandern und die vielfältigen Aufgaben in beliebiger Reihenfolge in Einzel-, Partner- oder auch Gruppenarbeit erledigen können. Jeder Lernzirkel ist als Übungseinheit zu verstehen, aber nicht als Einführung in diesen Themenbereich gedacht. Außerdem sollten die Schüler den sicheren Umgang mit dem Geodreieck und dem Koordinatensystem beherrschen. Ein Lernzirkel beinhaltet folgende drei Lernphasen: 1. Lernphase: Die Schülerinnen und Schüler durchlaufen in beliebiger Reihenfolge und individuellem Arbeitstempo alle Stationen und tragen die Lösungen in die Arbeitsblätter ein. (Die Arbeitsblätter sind so konzipiert, dass alle Schüler auch alle Stationen anlaufen müssen.) Der wechselnde Arbeitsplatz an den einzelnen Stationen schafft Abwechslung und kommt dem motorischen Bedürfnis der Schülerinnen und Schüler entgegen. 2. Lernphase: Am Ende aller Stationen haben die Schülerinnen und Schüler die Möglichkeit, ihre Arbeit an den Lösungsstationen sofort zu kontrollieren und die erreichten Punkte in ihre Arbeitsblätter einzutragen. Diese selbstständige Leistungskontrolle gewährleistet einen reibungslosen Ablauf und lässt unterrichtsfremde Aktivität kaum entstehen. 3. Lernphase: An der Station „Wie sicher bist du?“ (Kontrollstation) erfahren die Schülerinnen und Schüler eine individuelle Beurteilung, die ihnen einen Überblick über ihre Leistung ermöglicht und sie zum weiteren Training motiviert. Die Kopiervorlagen umfassen fünf thematisch geordnete Lernzirkel: Lernzirkel Lernzirkel Lernzirkel Lernzirkel Lernzirkel ������ A: B: C: D: E: Grundlagen der Geometrie Winkel Dreieck Viereck Kreis Albrecht Schiekofer: Lernzirkel EbeneKreis Geometrie Albrecht Schiekofer: Lernzirkel Persen Verlag GmbH, Buxtehude © Persen Verlag GmbH, Buxtehude 69 15 Anleitung (2) Jede Station ist so konzipiert, dass sich sowohl Arbeitsauftrag (oberer Teil) als auch Lösung (unterer Teil) auf einer Stationskarte befinden. Diese kann entweder gefaltet und laminiert werden (Möglichkeit A) oder auf ein Stationsschild (quer gefalteter DIN-A4-Karton) geklebt werden (Möglichkeit B). Es bietet sich zusätzlich an, Vorderund Rückseite verschiedenfarbig zu gestalten um Arbeitsauftrag und Lösung optisch noch stärker zu unterscheiden. Möglichkeit A: Vorderseite Rückseite Möglichkeit B: Vorderseite Rückseite Jedem Lernzirkel liegen Arbeitsblätter bei, die für die Schülerinnen und Schüler zur Bearbeitung kopiert werden müssen und dann den Ablauf des Lernzirkels unterstützen und erleichtern. Mithilfe der Arbeitsblätter allein kann nicht gearbeitet werden, da die einzelnen Arbeitsaufträge nur an den jeweiligen Stationen zu erfahren sind. So sind die Schülerinnen und Schüler angehalten, wirklich jede Station zu durchlaufen. Pro Station können maximal 5 Punkte erreicht werden. Die Gesamtpunktzahl eines Zirkels liegt also immer bei 50 Punkten. Viel Spaß und Erfolg bei der Arbeit mit dem Lernzirkel Mathematik „Ebene Geometrie“ wünscht Albrecht Schiekofer ������ Albrecht Schiekofer: Lernzirkel EbeneKreis Geometrie Albrecht Schiekofer: Lernzirkel Persen Verlag GmbH, Buxtehude © Persen Verlag GmbH, Buxtehude 70 16 Lernzirkel – räumlicher Aufbau Station 3 Station 6 Albrecht Schiekofer: Lernzirkel EbeneKreis Geometrie Albrecht Schiekofer: Lernzirkel Persen Verlag GmbH, Buxtehude © Persen Verlag GmbH, Buxtehude Station 5 Station 4 Station 8 Station 7 ������ Station 1 Station 2 Kontrollstation Station 9 Station 10 71 17