Brückenkurs Schulmathematik 9. Veranstaltung: Geometrie 5

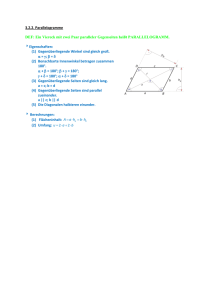
Brückenkurs Schulmathematik
9. Veranstaltung: Geometrie 5: Vierecke, Kreise
21. Juni 2012
1.Vierecke
1. Aufgabe: Ordnen Sie den Definitionen die entsprechenden Begriffe zu:
Ein Viereck, das ein Symmetriezentrum hat
Quadrat
Ein Viereck, das symmetrisch zu einer
Diagonalen ist
Rechteck
Ein Viereck, das symmetrisch zu beiden
Diagonalen ist
Raute
Parallelogramm
Drachenviereck
Ein Viereck, das symmetrisch zu den
Mittelsenkrechten und Diagonalen ist
Ein Viereck, das symmetrisch zu den
Mittelsenkrechten aller Seiten ist
2. Aufgabe: Was kann man über die Winkel in den oben genannten Vierecken aussagen?
3. Aufgabe: Die parallelen Seiten eines Trapezes sind 4 bzw. 12 cm lang, die Schenkel 8
bzw. 10 cm. Wie lang sind die Seiten des Ergänzungsdreiecks (hierzu siehe Abbildung)?
In welchem Verhältnis werden die Diagonalen des Trapezes durch ihren Schnittpunkt
geteilt?
Abbildung 1: Ergänzungsdreieck des Trapezes ABCD
* Wie groß ist der Flächeninhalt des Trapezes?
1. Aufgabe: In der Raute ABCD sei P ein beliebiger Punkt auf der Diagonalen AC: Es ist zu
2
2
zeigen, dass der Zusammenhang AB − PB = AP ⋅ PC besteht!
2. Aufgabe: Beweisen Sie folgende zwei Sätze:
a. Ein Viereck ist genau dann Sehnenviereck, wenn die Summe von zwei
gegenüberliegenden Winkeln 180° ist.
b. Ein Viereck ist genau dann Tangentenviereck, wenn die Summe der Längen
zweier gegenüberliegenden Seiten gleich der Summe der Längen der beiden
anderen gegenüberliegenden Seiten ist.
3. Aufgabe: Welche der folgenden Aussagen sind richtig? Begründen Sie Ihre Meinung!
a. Jedes gleichschenkliges Trapez ist ein Sehnenviereck.
b. Ein Quadrat hat genau zwei Symmetrieachsen.
c. In einem Parallelogramm ergänzen sich die gegenüber liegenden Winkel stets
zu 180°.
d. Ein Rechteck hat zwei Symmetrieachsen.
e. Ein Rechteck ist nicht punktsymmetrisch.
f. In einer Raute ergänzen sich die benachbarten Winkel stets zu 180°.
g. Jede Raute ist ein Tangentenviereck.
h. Jedes Rechteck ist ein Tangentenviereck.
i. Jedes Parallelogramm ist ein Sehnenviereck.
j. Jedes Drachenviereck ist eine Raute.
k. Jede Raute ist ein Drachenviereck.
l. Jedes Quadrat ist ein Parallelogramm.
2. Kreise
4. Aufgabe: Tragen Sie die Begriffe in die Abbildung 2 ein:
Mittelpunkt Radius Durchmesser Kreispunkt innerer Punkt
Tangente Sekante Sehne Passante Kreissektor Kreissegment
äußerer Punkt
Abbildung 2: Kreis
5. Aufgabe: Formulieren Sie den Peripheriewinkelsatz! Zeigen Sie, dass der Satz des Thales
ein Spezialfall des Peripheriewinkelsatzes ist!
6. Aufgabe: Tangentenkonstruktionen:
a. Konstruieren Sie die Tangente an den Kreis k von einem Punkt P, der
außerhalb des Kreises k liegt.
b. Im Zusammenhang mit der Aufgabe 3 vom Arbeitsblatt 6 haben wir bereits
wiederholt, wie man die gemeinsamen äußeren Tangenten an zwei Kreise k1
und k2 mit den Mittelpunkten M1 und M2 und den Radien r1 und r2 (r2 >r1)
konstruiert. Konstruieren Sie nun die gemeinsamen inneren Tangenten an zwei
Kreise k1 und k2 mit den Mittelpunkten M1 und M2 und den Radien r1 und r2 (r2
>r1)! Was passiert (überlegen Sie für beide Fälle), wenn die Radien der Kreise
gleich lang sind?
7. Aufgabe: Zeigen Sie mithilfe der Ähnlichkeit, dass der sog. Sekantensatz gilt: Sind A, B,
C und D vier Punkte auf einem Kreis, sodass sich die Sekanten AB und CD in einem Punkt
P außerhalb des Kreises schneiden, dann gilt: PA ⋅ PB = PC ⋅ PD . Als Spezialfall für
2
A=B ergibt sich der sog. Tangentensatz: PA = PC ⋅ PD . Ebenfalls mithilfe der
Ähnlichkeit ist zu zeigen, dass der sog. Sehnensatz gilt: Sind A, B, C und D vier Punkte
auf einem Kreis, sodass sich die Sehnen AC und BD in einem Punkt P außerhalb des
Kreises schneiden, dann gilt: PA ⋅ PC = PB ⋅ PD .
8. Aufgabe: Vom Punkt P ist der Tangentenabschnitt an einen Kreis 4 cm lang. Der Abstand
von P und dem Kreismittelpunkt beträgt 6 cm. Durch P wird eine Sekante gelegt, deren
längerer Abschnitt 8 cm ausmacht. Wie groß ist der Abstand dieser Sekante vom
Kreismittelpunkt? (In: Dönszne, Buvari Nora et al (2000): Kompendium. Temporg:
Budapest, S. 178)
Die nachfolgenden Aufgaben wurden in Anlehnung an Cukrowitz et al. (2006): Mathenetz
10 Gymnasium. Braunschweig: Westermann. formuliert.
9. Aufgabe: Der Radius eines Kreises wird verdoppelt. Wie wirkt sich das auf seinen
Umfang bzw. seinen Flächeninhalt aus? Der Flächeninhalt/der Umfang eines Kreises wird
verdoppelt. Wie wirkt sich das jeweils auf die beiden anderen Größen aus?
10.
Aufgabe: Bestimmen Sie den Winkel im Bogenmaß x bzw. im Gradmaß ϕ.
a. ϕ = 40°
b. ϕ = 160°
c. x = 0,8
d. x = 2,5
11. Aufgabe: Leiten Sie eine Formel her, die den Flächeninhalt A eines Kreises
a. in Abhängigkeit von Durchmesser d,
b. in Abhängigkeit vom Umfang u angibt.
12. Aufgabe: Berechnen Sie den Flächeninhalt einer ringförmigen Fläche, die zwischen
zwei konzentrischen Kreisen mit den Radien r1 = 5 cm und r2 = 7 cm entsteht. Wie
ändert sich die Fläche, wenn bei gleichem Außenradius die Ringdicke 1 cm beträgt?
Verallgemeinern Sie beide Aufgabenstellungen!