Blatt 5

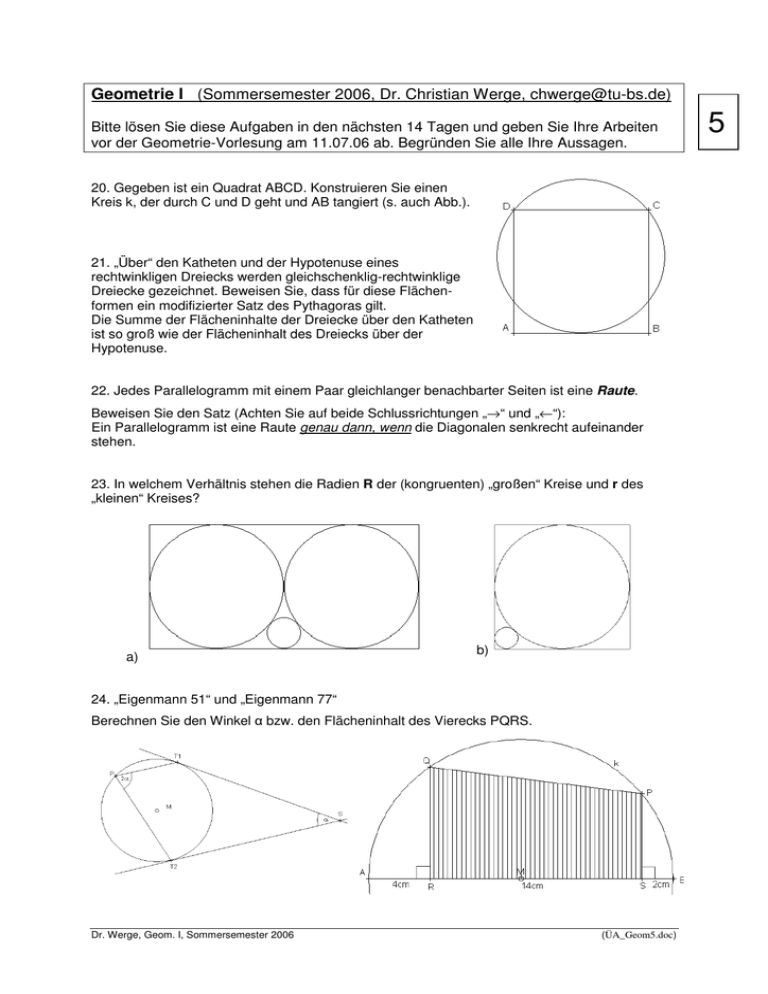
Geometrie I (Sommersemester 2006, Dr. Christian Werge, [email protected])
Bitte lösen Sie diese Aufgaben in den nächsten 14 Tagen und geben Sie Ihre Arbeiten
vor der Geometrie-Vorlesung am 11.07.06 ab. Begründen Sie alle Ihre Aussagen.
20. Gegeben ist ein Quadrat ABCD. Konstruieren Sie einen
Kreis k, der durch C und D geht und AB tangiert (s. auch Abb.).
21. „Über“ den Katheten und der Hypotenuse eines
rechtwinkligen Dreiecks werden gleichschenklig-rechtwinklige
Dreiecke gezeichnet. Beweisen Sie, dass für diese Flächenformen ein modifizierter Satz des Pythagoras gilt.
Die Summe der Flächeninhalte der Dreiecke über den Katheten
ist so groß wie der Flächeninhalt des Dreiecks über der
Hypotenuse.
22. Jedes Parallelogramm mit einem Paar gleichlanger benachbarter Seiten ist eine Raute.
Beweisen Sie den Satz (Achten Sie auf beide Schlussrichtungen „→“ und „←“):
Ein Parallelogramm ist eine Raute genau dann, wenn die Diagonalen senkrecht aufeinander
stehen.
23. In welchem Verhältnis stehen die Radien R der (kongruenten) „großen“ Kreise und r des
„kleinen“ Kreises?
a)
b)
24. „Eigenmann 51“ und „Eigenmann 77“
Berechnen Sie den Winkel α bzw. den Flächeninhalt des Vierecks PQRS.
Dr. Werge, Geom. I, Sommersemester 2006
(ÜA_Geom5.doc)
5