Strahlensätze Einführung

Strahlensätze
Einführung
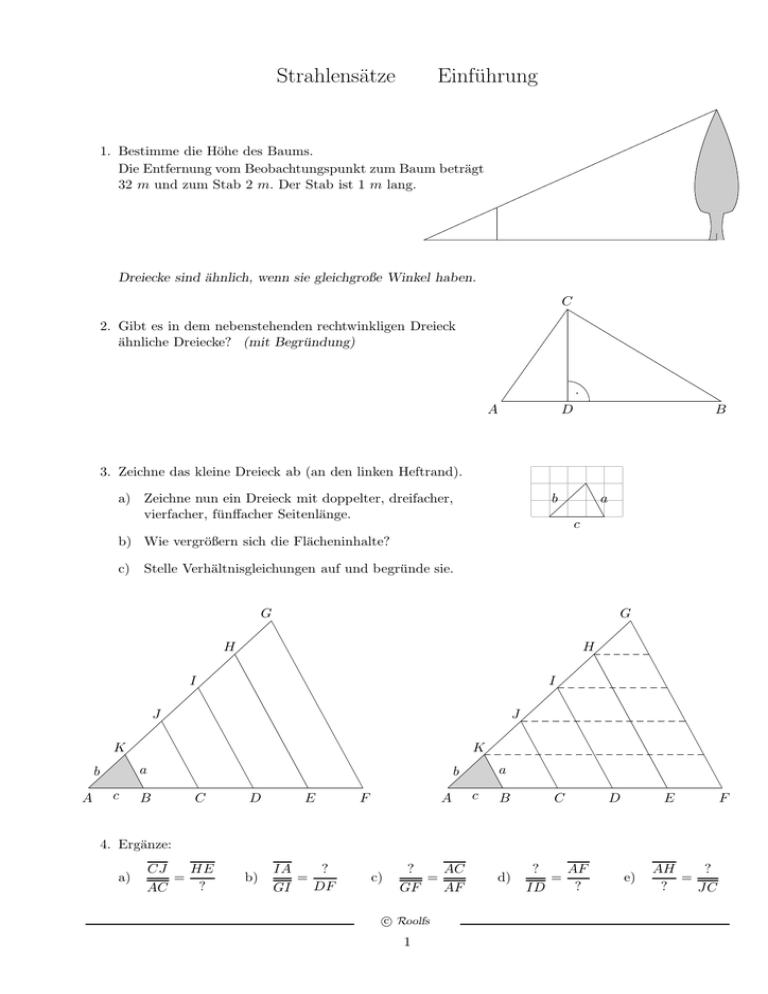
1. Bestimme die Höhe des Baums.
Die Entfernung vom Beobachtungspunkt zum Baum beträgt
32 m und zum Stab 2 m. Der Stab ist 1 m lang.
Dreiecke sind ähnlich, wenn sie gleichgroße Winkel haben.
C
2. Gibt es in dem nebenstehenden rechtwinkligen Dreieck
ähnliche Dreiecke? (mit Begründung)
A
D
·
B
3. Zeichne das kleine Dreieck ab (an den linken Heftrand).
a) Zeichne nun ein Dreieck mit doppelter, dreifacher,
vierfacher, fünffacher Seitenlänge.
a
b
c
b) Wie vergrößern sich die Flächeninhalte?
c) Stelle Verhältnisgleichungen auf und begründe sie.
G
G
H
H
I
I
J
J
K
a
b
A
K
c
B
a
b
C
D
E
F
A
c
B
C
d)
?
AF
=
?
ID
D
E
4. Ergänze:
a)
CJ
HE
=
?
AC
b)
IA
?
=
DF
GI
c)
?
AC
=
GF
AF
c Roolfs
1
e)
AH
?
=
?
JC
F
Strahlensätze
Einführung
Lösungen
1. Um an Bekanntes anzuknüpfen, zeichnen wir ein Koordinatensystem ein.
1
Die Steigung der Strecke zur Baumspitze beträgt m = 2 .
Mit h als Baumhöhe ist daher:
1
h
2 = 32
=⇒
h = 16 (m)
h
1
|
2
{z
32
}
C
2. Die Dreiecke ∆ ABC und ∆ ADC sind ähnlich, da sie im
rechten Winkel und in α übereinstimmen. Der Nachweis der
Übereinstimmung in 2 Winkeln genügt (warum?).
Desgleichen sind auch ∆ ABC und ∆ BCD ähnlich.
Dann müssen aber auch ∆ ADC und ∆ BCD ähnlich sein.
α
A
D
·
B
3. a)
b) Die Flächeninhalte wachsen mit dem Quadrat des Faktors an.
c) Es gilt z. B.
G
KB
HE
=
AB
AE
| {z }
| {z }
a
4
a
=
c
c
4
oder
AC
AJ
=
CF
JG
| {z }
| {z }
2c/
2b/
=
3c/
3b/
H
I
J
K
a
b
A
c
B
C
D
E
F
4.
a) AE
b) AD
c) JC
d) AD, GF
oder umgekehrt
c Roolfs
2
e) EH, AJ
oder umgekehrt
Strahlensätze
a
d
=
b
c
1.
AC
AD
=
a
d
c
f
g
=
a
AC
2.
D
E
g
d
f
A
a
f kg
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
gegeben:
a, b, d
a, b, c
AB, AC, d
AC, b, d
d, c, AC
a, b, AD
a, b, g
AD, c, f
f, g, b
AD, c, a
c, AD, f
f, g, c
gesucht:
3
13. Setze für x in den Term
x3
x2
− 4
c
d
c
c
b
d
f
g
a
AC
g
AD
ein:
a) −1
2
b) 3
√
c) 3 2
d) −3
√
e) 2 3
c Roolfs
3
B
b
C
Strahlensätze
a
d
=
b
c
1.
2.
AC
AD
=
a
d
1. c =
d·b
a
2. d =
a·c
b
3. c =
(AC − AB) · d
AB
4. c =
b·d
AC − b
5. b =
c · AC
d+c
6. d =
a · AD
a+b
7. f =
a·g
a+b
8. g =
f · AD
AD − c
9. a =
b·f
g−f
D
c
f
g
=
a
AC
E
g
d
f
A
a
B
b
f kg
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
gegeben:
a, b, d
a, b, c
AB, AC, d
AC, b, d
d, c, AC
a, b, AD
a, b, g
AD, c, f
f, g, b
AD, c, a
c, AD, f
f, g, c
13. Setze für x in den Term
gesucht:
3
x2
c
d
c
c
b
d
f
g
a
AC
g
AD
C
10. AC =
11. g =
AD · f
AD − c
12. AD =
ein:
x3 − 4
a) −1
13. a)
2
b) 3
√
c) 3 2
d) −3
√
e) 2 3
c Roolfs
4
AD · a
AD − c
c·g
g−f
12
−5
b)
81
5
c)
6
√
108 2 − 9
d)
−
e)
1
√
8 3−1
4
39
Startseite
5