Aehnlichkeit_Anwendungen_A

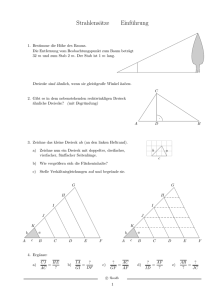
Gymnasium Pegnitz
Wiederholung JS 8
Juli 2007
Ähnlichkeit: Anwendungen (Aufgaben)
1. Untersuche, ob man aus den angegebenen Beziehungen auf die Ähnlichkeit der Dreiecke ABC und RST schließen kann. Wenn ja, nach welchem Ähnlichkeitssatz?
(a) b : c = s : r,
(b) α = ρ,
α=τ
β=τ
b
α
A
C
γ
.
......
... ..
.... .....
....
..
.
.
.... ..............................
..
....
..
....
.
.
........
.
......
... ....
...
.... ....
..
.
.
.
.
.
.
.
.
................................................................................
c
a
β
T
τ
.....
.... ...
.... .....
...
...
.
.
.
.
.. .....
.
.... .........................
....
...
....
.
.
..... ...
.
... .....
... .....
.
.
.
...
..
..
...
.
.
.
...............................................................................
s
ρ
B
R
2. Gegeben ist ein beliebiges Sehnenviereck ABCD
(vgl. Skizze).
r
σ
t
D
S
C
.....................................
...
................................
..... .. .......... ..................................
......
.... ....
...........
.
.
......
..... .... .............................
.
... ....
.
.
.
...............
.
..... ..... .. ..........
.
............... .....
...
.
..
...
.. ......
............... .........
.
.
.
....
.
...
............. ...
..... .. ..
...
.
..
.
............
..
.
.
.
.
.
.
.
.
.
.
.
...... ....
........ .
.
....
.
...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..........
... ...
...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... .. .......
......... ...
... ... ...... .......................
.
...........................
...
...........
...
.....
.....
......
......
.
.........
.
.
.
.
.
......................
T
(a) Zeige: Die Dreiecke AT C und DBT sind
ähnlich.
B
A
(b) Beweise: AT · BT = DT · CT
3. Zwei Kreissehnen [AC] und [DP ] schneiden
sich in einem Punkt P .
(a) Beweise: Die Dreiecke BCP und DP A
sind ähnlich.
(b) Leite daraus folgende Gleichung her:
u·v =x·y
...............................
....................
..........
..........
.........
........
.......
.......
.
......
.
.
.
.
......
....
.
.
.
.
.....
.
....
.....
.
.
.
.
.....
...
.
.
.
...
.........
.
.
.
.
.
................. .....................
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
.
..................
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
.
.
.
.
.
.
.
.
..
..................................................
.
...
.
.
.
.
....
...
....
.......
...
....
.. .......
.
.
.
...
....
..
.
..
.
...
.
.
....
.
..
.
.
...
.
.
.
.
.
....
.
...
...
.
...
.
....
...
...
....
.
...
.
....
..
..
.
.
.
....
....
...
...
.
...
....
.
..
...
....
...
.
.
.
....
..
.
..
.
.
.....
....
..
.
.
....
.
....
..
...
.
...
....
.
.
.
.
....
.
...
...
.
.
.
.
.... ....
...
.... ....
...
...
..
...
...
.......
..
.... .......
...
..
...
.
.
.
.
...
.
.
....
.
..
...
....
...
....
...
...
....
...
....
...
..
....
....
...
...
....
.
.
.
.
...
.
.
.
....
.
...
...
....
...
...
...
....
....
....
....
....
.... .......
...
....
..... ...
....
.
.
.
.
.
.
.
..............................
...
.....
..........................................
......
..........................................................
......
...
.......
........
.......
..........
........
.
.
.
.
.
.
.
.................
.
.
.
..................................
D
A
v
x
P
u
y
B
4. Im gleichschenkligen Dreieck ABC ist γ = 36o ,
AB = 3, 0 cm und AC = 4, 9 cm.
(a) Zeige, daß die Halbierende des Basiswinkels
6< BAC das Dreieck ABC so zerlegt, daß ein
Teildreieck dem ganzen Dreieck ähnlich ist.
(b) Berechne AD, DC und BD!
C
C
......
... ...
... ....
.... ....
...
..
...
...
.
........ .......
.. .......... ....
.
...
....
...
.
.
...
...
...
..
...
.
...
....
...
.
.
...
....
...
.
.
...
..
...
.
...
....
...
.
.
..
....
.........
.
.
.
.
.
.
.... ....
.
.
.
.
....
...
...
.
.
.
.
.
.
.
...
...
.....
...
...
......
...
...
......
.
..
.
...
.
.
.
...
.
...
.
..
.
.
.
.
....
...
.
..
.
.
.
.
...
...
.
.
.
.
.
....
...
....
.
.
.
.
.
.
...
..
...
.... ...........
..
..........
...............................................................................................................
γ
D
A
1
B
5. Beweise den Satz: Die Längen der Höhen von zwei Ecken eines Dreiecks verhalten
sich wie die Abstände ihrer Fußpunkte von der dritten Ecke.
6. In einem Dreieck ABC gilt die Winkelbeziehung γ = 2α. Die Winkelhalbierende wγ
trifft [AB] in D.
(a) Begründe anhand einer übersichtlichen Skizze genau, daß eines der beiden entstehenden Teildreiecke zum ganzen Dreieck ähnlich ist!
(b) Gib die entsprechenden Streckenverhältnisse im jeweils ähnlichen Dreieck an:
CD : BC = ? ;
AB : BC = ?
7. Im Dreieck ABC betragen die Winkel α = 400 und β = 600 . Beweise: Die Winkelhalbierende wγ zerlegt das Dreieck in zwei Teildreiecke, von denen eines zum ganzen
Dreieck ähnlich ist.
8. Das Dreieck ABC ist rechtwinklig mit einem rechten Winkel bei C. Der Fußpunkt
D der Höhe h zerlegt [AB] in zwei Abschnitte der Längen p und q.
C
(a) Zeige: Die Dreiecke ADC und
............
.. .. ...
... .. ...........
......
... ...
......
... ....
.
.
..
..
...
.... ...........
.....
............... .... .......2
......
.
.
.
.1
.............
......
..
.
.
......
.
..
..
......
.
.
.
....
......
..
.
.
......
..
....
.
......
.
...
..
......
.
.
......
..
..
.
.
.
......
...
..
.
......
.
..
......
..
.
.
.
...
......
..
.
......
.
.
.
..
......
.
.
.
.
..
......
..
.
.
.
......
....
........
.
.....
.
.
.. ....
.
.
........
.
...
....
..
.. ..........
.
.
..
......
..
..................
.
.
...
..
.
.
.
...
.
.
..............................................................................................................................................................................................................................................
CDB sind ähnlich.
γ γ
(b) Folgere daraus: h2 = pq.
h
α
A
9. Der Schüler in nebenstehender Abbildung hält seinen Kopf so, daß er die
Baumspitze in dem am Boden liegenden
Spiegel sehen kann.
Bei der Reflexion des Lichtes am Spiegel
gilt das Reflexionsgesetz: α = β .
(a) Berechne die Höhe h des Baumes!
(b) Bei einem Sturm brechen die oberen 35, 75 m des Baumes ab. In
welcher Entfernung x vom Schüler
muß jetzt der Spiegel liegen, damit
er darin, bei gleichem Standort wie
vorher, die neue Baumspitze sehen
kann?
2
q q
p
D
q
β
B
. ........................................
...
.......
... ............
.
.
. ....
... .........
... .. .. ..
... .... .... ......
.
... ...................
.
...
.. ... ..
...
..
... .... ....
.
.
... .... ....
...
.
.
.
.
.. .... ...
...
... ... ....
...
...
... ... ...
...
........... .... ............
.
.
.
.. .. ...
...
.. ... ..
...
.. .. ...
...
... ... ....
...
.
.
.
.. .. ..
.. .... ....
...
..
...
...
..
..
..
..
..
..
..
...
.
.
h
....
.
.
..
..
...
..
...
..
...
...
.
.
.
.
.
...
......
............
...
.
.
.
.
............. ... .................
.
...
.... ... ....
...
.. .. ..
...
... .... .....
...
.
.
.. ... ..
.
...
... .... ....
...
.. .... ....
..
...
....
.
.
... ... ...
..
...
...
..
... ... ...
... 90 ...
...
.... .... ....
... cm ...
...
..
.... .... ....
...
.
..
.. ..
...
...
......................................
... ... ...
...
...
..
..
... .... ....
.
.. ...
165 ........................... ...... ........
.... ..... .....
.. .. ..
.. .... .. ...
cm
.. .. ..
.. .... ....
.....
.. ... α ........ β
... .. ..
......................................................................................................................................................................................................................................................
..
..
....... ...
...
24 m
.
Spiegel ...
6
c
6
?
-
?