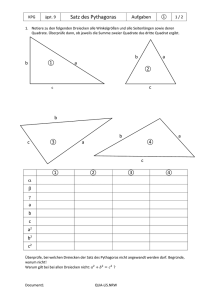
Umkehrung des Satzes von Pythagoras

Arbeitsblatt: Umkehrung des Satzes von Pythagoras
Mathematik / Geometrie / Berechnungen an Dreiecken / Satz des Pythagoras
Arbeitsblätter zum Ausdrucken von sofatutor.com
Umkehrung des Satzes von Pythagoras
1
Beschreibe, wie du mit einem Seil einen rechten Winkel konstruieren kannst.
2
Berechne, ob das Dreieck mit den Seiten a = 3
3
Schildere, wie du die Umkehrung des Satzes des Pythagoras anhand eines Dreiecks mit den
Seitenlängen a = 5 cm, b = 12 cm und c = 13 cm anwenden kannst.
4
Erkläre, wie ein Tischler zwei Leisten mit einem Zollstock rechtwinklig ausrichten kann.
5
Ermittle, bei welchen Dreiecken es sich um rechtwinklige handelt.
6
Entscheide, welche Dreiecke spitzwinklig, rechtwinklig oder stumpfwinklig sind.
+
mit vielen Tipps, Lösungsschlüsseln und Lösungswegen zu allen Aufgaben
cm, b = 10 cm und c = 7 cm rechtwinklig ist.
Das komplette Paket, inkl. aller Aufgaben, Tipps, Lösungen und Lösungswege
gibt es für alle Abonnementen von sofatutor.com
Schau das Video zur Aufgabe: http://www.sofatutor.com/v/1FN/aRK
© 2016 sofatutor GmbH, Berlin. Alle Rechte vorbehalten. V6435
1
Arbeitsblatt: Umkehrung des Satzes von Pythagoras
Mathematik / Geometrie / Berechnungen an Dreiecken / Satz des Pythagoras
von 6
Beschreibe, wie du mit einem Seil einen rechten Winkel konstruieren
kannst.
Bringe die Schritte in die richtige Reihenfolge.
A
Wir knicken zunächst nach drei Markierungen.
B
Nun legen wir das letzte Stück so, dass es wieder auf dem Anfangspunkt liegt.
C
Erneut knicken wir nach vier Markierungen.
D
Mit der Umkehrung des Satzes des Pythogoras ist der Winkel zwischen den kürzesten Seiten gerade ein rechter Winkel.
Das machen wir uns nun für die Konstruktion zunutze.
E
Für a
2
2
2
= 3 cm, b = 4 cm und c = 5 cm gilt in der Tat3 + 4 = 5 = 25.
F
Wir setzen im gleichen Abstand insgesamt 3 + 4 + 5
= 12 Markierungen.
G
Wir überlegen uns ein möglichst einfaches Dreieck, für dasa2
RICHTIGE REIHENFOLGE
Schau das Video zur Aufgabe: http://www.sofatutor.com/v/1FN/aRK
© 2016 sofatutor GmbH, Berlin. Alle Rechte vorbehalten. V6435 | E4503
+
b2
=
c2 gilt.
Arbeitsblatt: Umkehrung des Satzes von Pythagoras
Mathematik / Geometrie / Berechnungen an Dreiecken / Satz des Pythagoras
Unsere Tipps für die Aufgaben
1
von 6
Beschreibe, wie du mit einem Seil einen rechten Winkel
konstruieren kannst.
1. Tipp
Am Anfang tätigen wir eine Vorüberlegung, wie wir die Umkehrung Satz des Pythagoras anwenden wollen.
2. Tipp
Wir müssen erst die Markierungen setzen, bevor wir das Seil legen können.
Schau das Video zur Aufgabe: http://www.sofatutor.com/v/1FN/aRK
© 2016 sofatutor GmbH, Berlin. Alle Rechte vorbehalten. V6435
Arbeitsblatt: Umkehrung des Satzes von Pythagoras
Mathematik / Geometrie / Berechnungen an Dreiecken / Satz des Pythagoras
Lösungen und Lösungswege für die Aufgaben
1
von 6
Beschreibe, wie du mit einem Seil einen rechten Winkel
konstruieren kannst.
Lösungsschlüssel: G, E, D, F, A, C, B
Im alten Ägypten (um 2000 v. Chr.) mussten jedes Jahr nach der Nilüberschwemmung die Felder neu
vermessen werden. Dies taten Vermessungsbeamten, auch "Seilspanner" oder Harpedonapten genannt.
Sie benutzten dazu sogenannte Knotenschnüre mit Knoten in gleichen Abständen. Sie mussten rechteckige
Felder abstecken und nutzen ihre Seilschnüre, um rechte Winkel zu konstruieren.
3, 4 und 5 ist mit der Umkehrung des Satzes des Pythagoras gerade ein
+ 42 = 52 = 25 gilt.
Ein Dreieck mit den Kantenlänge
rechtwinkliges Dreieck, da ja 32
Die Schnellspanner mussten also nur ein Dreieck legen, dass die Kantenlänge von 3, 4 und
aufweist. Der Winkel, der der längsten Seite gegenüberliegt, ist dann ein rechter Winkel.
Schau das Video zur Aufgabe: http://www.sofatutor.com/v/1FN/aRK
© 2016 sofatutor GmbH, Berlin. Alle Rechte vorbehalten. V6435
5 Einheiten