2.2.1 Elektronenstrahloszilloskop (EO) - schruefer

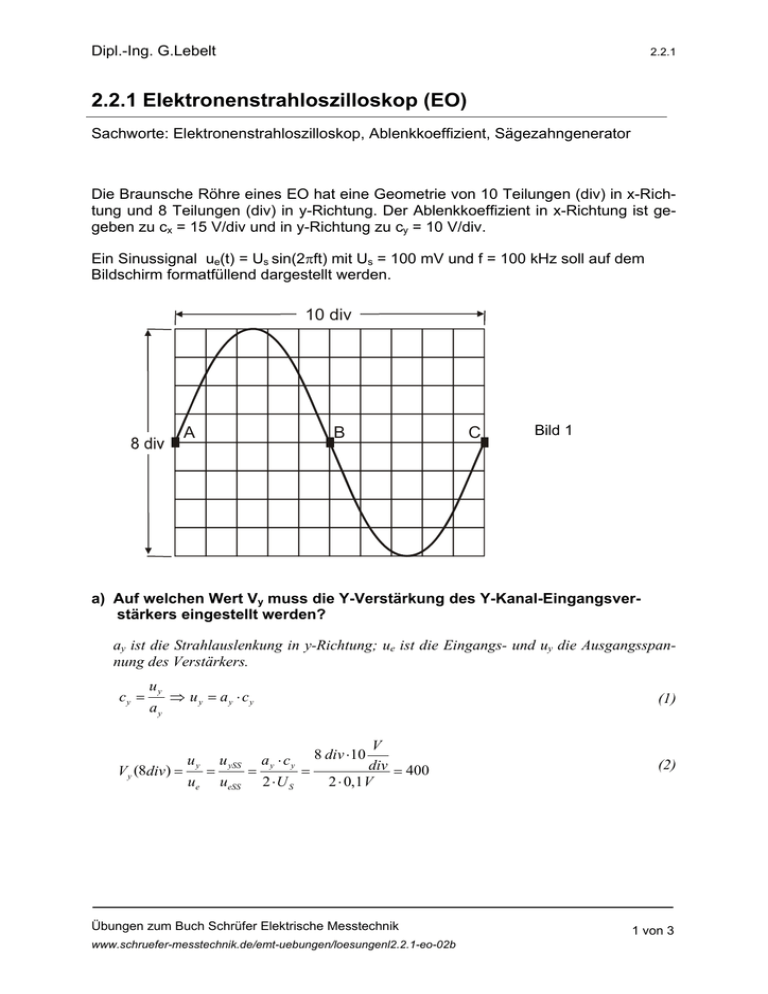
Dipl.-Ing. G.Lebelt
2.2.1
2.2.1 Elektronenstrahloszilloskop (EO)
Sachworte: Elektronenstrahloszilloskop, Ablenkkoeffizient, Sägezahngenerator
Die Braunsche Röhre eines EO hat eine Geometrie von 10 Teilungen (div) in x-Richtung und 8 Teilungen (div) in y-Richtung. Der Ablenkkoeffizient in x-Richtung ist gegeben zu cx = 15 V/div und in y-Richtung zu cy = 10 V/div.
Ein Sinussignal ue(t) = Us sin(2πft) mit Us = 100 mV und f = 100 kHz soll auf dem
Bildschirm formatfüllend dargestellt werden.
10 div
B
A
C
Bild 1
a) Auf welchen Wert Vy muss die Y-Verstärkung des Y-Kanal-Eingangsverstärkers eingestellt werden?
ay ist die Strahlauslenkung in y-Richtung; ue ist die Eingangs- und uy die Ausgangsspannung des Verstärkers.
cy =
uy
ay
⇒ u y = ay ⋅ cy
Vy (8div) =
uy
ue
=
u ySS
ueSS
=
(1)
ay ⋅ cy
2 ⋅U S
=
V
div = 400
2 ⋅ 0,1 V
8 div ⋅10
Übungen zum Buch Schrüfer Elektrische Messtechnik
www.schruefer-messtechnik.de/emt-uebungen/loesungenl2.2.1-eo-02b
(2)
1 von 3
Dipl.-Ing. G.Lebelt
2.2.1
b) Skizzieren Sie den zeitlichen Verlauf der Sägezahnspannung ux(t) des Zeitablenkteiles und markieren Sie in diesem Diagramm die zu Bild 1 korrespondierenden Punkte A, B und C.
Im y-t-Betrieb soll in x-Richtung die Zeit abgelesen werden können. Dies wird durch eine
zeitproportionale Spannung an den x-Ablenkplatten erreicht (Bild 2).
Ux s s
ux (t)
t
T
A
Bildschirmrand:
links
B
C
Mitte
rechts
Bild 2
c) Welchen Spitze-Spitze-Wert UxSS und welche Anstiegsgeschwindigkeit
dux / dt muss die Ablenkspannung ux(t) aufweisen?
Aus dem Ablenkkoeffizienten berechnet sich die nötige Ablenkspannung in x-Richtung allgemein
cx =
Ux
⇒ nötige Ablenkspannung U x = ax ⋅ cx
ax
mit Strahlauslenkung ax
(3)
und zahlenmäßig für eine formatfüllende x-Auslenkung von 10 div:
U xSS (10 div) = ax ⋅ cx = 10 div ⋅15
V
= 150 V
div
(4)
Die Anstiegsgeschwindigkeit des Sägezahns ist konstant und berechnet sich zahlenmäßig
mit der Überlegung, dass die Ablenkzeit T gleich einer Periodendauer 1/f des darzustellenden Signals der Frequenz f sein muss.
du x Δu x U xSS
=
=
dt
Δt
T
du x U xSS
1
V
V
=
= U Z ⋅ f = 150 V ⋅100 ⋅103 = 1,5 ⋅107 = 15
μs
dt
T
s
s
Übungen zum Buch Schrüfer Elektrische Messtechnik
www.schruefer-messtechnik.de/emt-uebungen/loesungenl2.2.1-eo-02b
(5)
2 von 3
Dipl.-Ing. G.Lebelt
2.2.1
d) Zeichnen Sie eine Operationsverstärkerschaltung, die den zeitproportionalen Teil der Sägezahnspannung erzeugen kann.
IC
R
Ie
C
Bild 3
U=
OV
ux
e) Dimensionieren Sie diese Schaltung, wenn ihnen eine ideale 10 V-Gleichspannungsquelle U= zur Verfügung steht, der maximal ein Strom von 1 mA
entnommen werden darf.
Im Buch ist die Herleitung des Integrationsverstärkers zu finden. Dort wird die Ausgangsspannung des Verstärkers in Formel (2.208) hergeleitet. Mit den Größen nach Bild 3:
t
1
ux = −
U = dτ
RC ∫o
(6)
Für eine konstante über die Zeit t integrierte Spannung U= ergibt sich eine mit der Zeit t
linear abfallende Spannung, die sog. Sägezahnablenkspannung.
uz = −
1
U= ⋅ t
RC
(7)
Die Ableitung dieser Spannung
du x
1
=−
U=
dt
RC
(8)
wird nach RC aufgelöst und der Zahlenwert aus Gl. (5) eingesetzt.
RC =
U=
10V
10 ⋅10−6
2
s = μs
=
=
V
du x
15
3
15
μ
s
dt
(9)
Der Eingangswiderstand Re eines Integrators ist wie im Buch abgeleitet, gleich dem Widerstand R (siehe Bild in Punkt d)), der sich bei einer Eingangsspannung U= und einem
Eingangstrom Ie folgendermaßen berechnet:
Re = R =
U = 10 V
=
= 10 k Ω
I e 1 mA
(10)
Mit Gl. (9) und der Einheit 1 F = 1 As / V ergibt sich C zu:
C=
2
1 2
1
2
1
μs = μs
= ⋅10−6 s ⋅
= 66, 7 pF
R 3 10 k Ω 3
3
10 ⋅103 V / A
Übungen zum Buch Schrüfer Elektrische Messtechnik
www.schruefer-messtechnik.de/emt-uebungen/loesungenl2.2.1-eo-02b
(11)
3 von 3