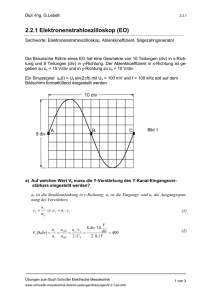
Grundgleichungen der Elektrostatik

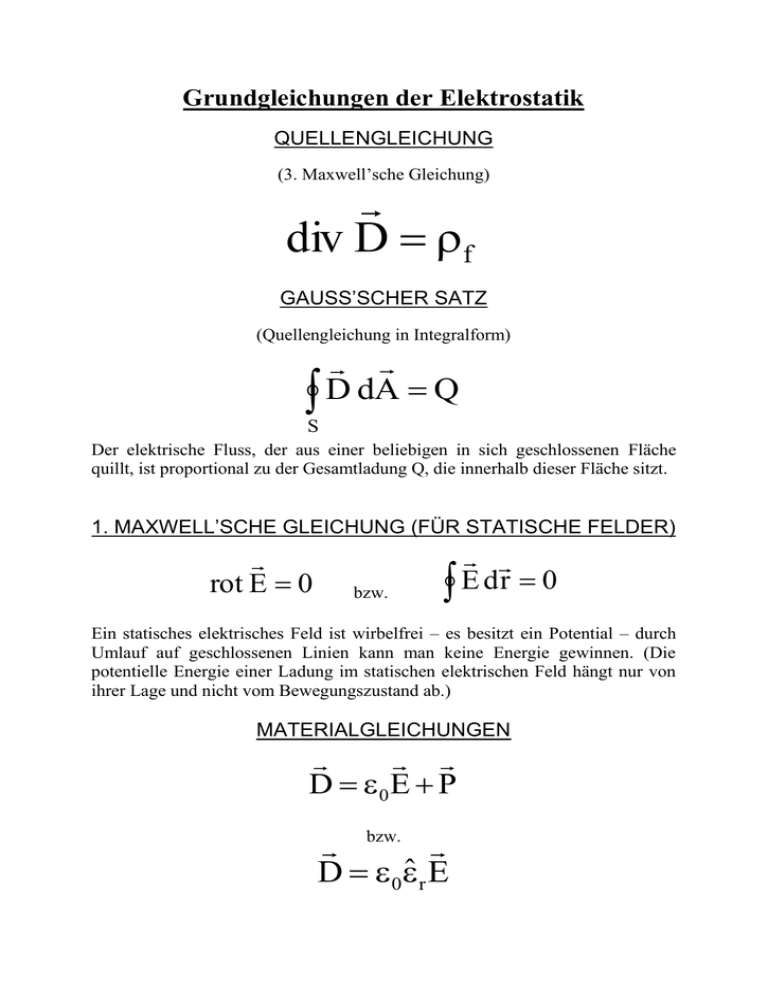
Grundgleichungen der Elektrostatik
QUELLENGLEICHUNG
(3. Maxwell’sche Gleichung)

div D  f
GAUSS’SCHER SATZ
(Quellengleichung in Integralform)
 
 D dA  Q
S
Der elektrische Fluss, der aus einer beliebigen in sich geschlossenen Fläche
quillt, ist proportional zu der Gesamtladung Q, die innerhalb dieser Fläche sitzt.
1. MAXWELL’SCHE GLEICHUNG (FÜR STATISCHE FELDER)

rot E  0
bzw.
 
 E dr  0
Ein statisches elektrisches Feld ist wirbelfrei – es besitzt ein Potential – durch
Umlauf auf geschlossenen Linien kann man keine Energie gewinnen. (Die
potentielle Energie einer Ladung im statischen elektrischen Feld hängt nur von
ihrer Lage und nicht vom Bewegungszustand ab.)
MATERIALGLEICHUNGEN

 
D  0 E  P
 bzw. 
D  0ˆ r E
Der Integralsatz von Gauß – Ostrogradski
Für beliebige Vektorfelder gilt:
 

 E dA   div E dV

S
V
V ist das von der geschlossenen Fläche S eingeschlossene Volumen. Wegen
 
div E 
0
Erhält man mit

Q
dV


0
V 0
die Beziehung
 
 0  E dA  Q

S
In Medien (r > 1) gilt:
 
 D dA  Q

S
Der elektrische Fluss, der aus einer beliebigen in sich geschlossenen Fläche
quillt, ist proportional zu der Gesamtladung Q, die innerhalb dieser Fläche sitzt.