Lösungen - Mathe für jung und alt

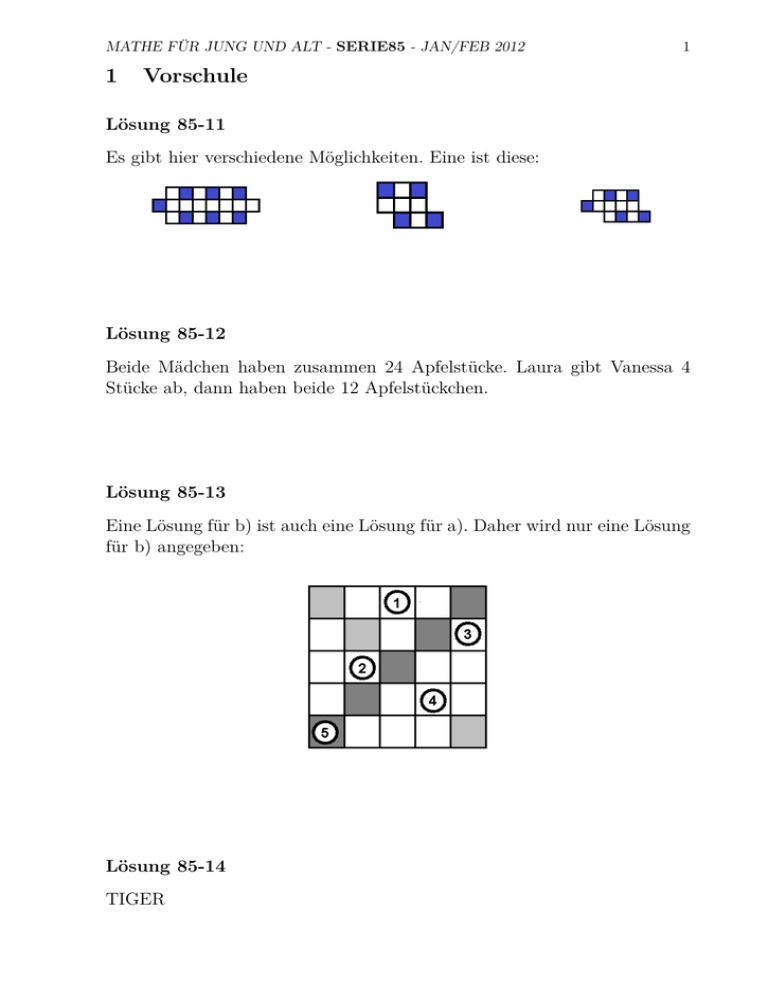
MATHE FÜR JUNG UND ALT - SERIE85 - JAN/FEB 2012
1
1
Vorschule
Lösung 85-11
Es gibt hier verschiedene Möglichkeiten. Eine ist diese:
Lösung 85-12
Beide Mädchen haben zusammen 24 Apfelstücke. Laura gibt Vanessa 4
Stücke ab, dann haben beide 12 Apfelstückchen.
Lösung 85-13
Eine Lösung für b) ist auch eine Lösung für a). Daher wird nur eine Lösung
für b) angegeben:
Lösung 85-14
TIGER
2
Heike Winkelvoß, www.egladil.de
Lösung 85-15
4 und 8
Lösung 85-16
Die Ziffern 4, 6 und 7 kommen genau viermal vor. Die Ziffer 5 kommt nur
dreimal vor.
Die größte dreistellige Zahl aus 4, 6 und 7 ist die 764.
2
Klassen 1 und 2
Lösung 85-21
a) Haufen A besteht aus 13 Steinen, Haufen B aus 17 Steinen
b) Es müssen 2 Steine umgelegt werden. Dann besteht jeder Haufen aus
15 Steinen.
Lösung 85-22
Antwort: Julia ist 12 cm kleiner als Sarah und 7 cm größer als Maike.
Begründung:
1 m und 36 cm + 7 cm = 1 m und 43 cm.
1 m und 55 cm − 12 cm = 1 m und 43 cm.
MATHE FÜR JUNG UND ALT - SERIE85 - JAN/FEB 2012
3
Lösung 85-23
A druckt Berlin (also A - 1)
C druckt Prenzlau (also C - 2)
I druckt Halle (also I - 3)
D druckt Erfurt (also D - 4)
Wanda, 6 Jahre, Klasse 2 und Jonah, 7 Jahre, Klasse 2 haben als
einzige festgestellt, dass die Stempelbilder von der Seite nicht stimmen
können, da z. B. der Querbalken vom H nicht mit gezeichnet ist.
Das finde ich ganz schön pfiffig!
Lösung 85-24
a) 2, 4, 6, 8, 10, 12, 14, 16,18, 20, 22, 24, 26, 28
b) 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52
c) 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70
d) 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120
e) 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39
f) 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72
g) 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88
Lösung 85-25
a) Weil immer 2 Seiten vom Würfel, die gegenüber liegen, 7 ergeben und
davon gibt es 6 bzw. 12 sichtbare Seiten an der Seite. Deswegen muss man
rechnen 6 · 7. Das sind 42 plus die Zahl oben drauf, von 1 bis 6. Das ergibt
43 bis 48 Augenzahlen.
b) Ich rechne 42 plus die Zahl oben. Dann habe ich das Ergebnis.
4
Heike Winkelvoß, www.egladil.de
Lösung 85-26
=5
Lösung 85-27
a) Sie braucht 2 Blätter.
b) 4 mal oder 2 mal, wenn sie die Blätter übereinander legt.
Lösung 85-28
Diese Aufgabe hat mehr als eine Lösung:
M >A>T <H<E>M >A>T >I<K
4>3>2<5<6>4>3>2>1<7
5>4>3<6<7>5>4>3>1<2
5>3>2<4<6>5>3>2>1<7
6>5>3<4<7>6>5>3>1<2
6>4>2<5<7>6>4>2>1<3
6>3>2<4<7>6>3>2>1<5
MATHE FÜR JUNG UND ALT - SERIE85 - JAN/FEB 2012
3
5
Klassen 3 und 4
Lösung 85-31
Eine mögliche Lösung ist
6 12 6 12
6 12 6 12
12 6 12 6
12 6 12 6
3
2
4
1
1
4
2
3
2
3
1
4
4
1
3
2
Lösung 85-32
Nein, denn wenn sie genau 5 Teile der Form a) hätte, wären das 5 · 3 = 15
kleine Quadrate. Die ganze Figur besteht aus 22 kleinen Quadraten. Für
Form b) blieben dann noch 22 − 15 = 7 kleine Quadrate. Figur b) besteht
aber aus 4 Quadraten und 7 ist nicht durch 4 teilbar.
Lösung 85-33
Er muss mindestens 7 Murmeln herausnehmen.
Begründung: Nachdem er 6 Murmeln herausgenommen hat, hat er im ungünstigsten Fall von jeder der 3 Farben gerade 2 erwischt. Mit der 7. Murmel nimmt er dann sicher die dritte einer der 3 Farben heraus.
Lösung 85-34
6
Heike Winkelvoß, www.egladil.de
13212, denn 12000 + 1200 + 12 = 13212.
Lösung 85-35
a) 365 · 10 · 24 · 4200 = 367920000 mal.
b) 365 · 60 · 24 · 4200 = 2207520000 mal.
Lösung 85-36
Es sind 91 Geldstücke.
Begründung: Man kann alle Teiler der Zahl 7 bis zur 100 durchprobieren,
welchen Rest sie bei Division durch 2, 3, 5 und 6 lassen. Nur die 91 lässt
jedes Mal den Rest 1.
Lösung 85-37
a) 24 = 2 · 2 · 2 · 3, also 1 · 24, 1 · 2 · 12, 1 · 3 · 8, 1 · 4 · 6, 2 · 2 · 6, 2 · 3 · 4 Das
sind 6 verschiedene Quader
b) 9 = 3 · 3 also 1 · 9, 1 · 3 · 3. Das sind zwei Möglichkeiten.
c) 1 · 1 · 11 Das ist nur eine Möglichkeit.
Lösung 85-38
Die Sonne ist zu sehen.
7
MATHE FÜR JUNG UND ALT - SERIE85 - JAN/FEB 2012
4
Klassen 5 und 6
Lösung 85-41
9999
9999
Lösung von Yuxuan Kong, 9 Jahre, Klasse 4:
100 = 99 +
111 − 11 + 1 − 1 · 1 · 1 · 1
22 · 2 · 2 + 2 + 2 + 2 + 2 + 2 + 2
33 · 3 + 3 − 3 + 3 − 3 : 3 − 3 : 3
5·5+5·5+5·5+5·5+5−5
66 + 6 · 6 − 6 + 6 − 6 : 6 − 6 : 6
7·7+7·7+7:7+7:7+7−7
=
=
=
=
=
=
100
100
100
100
100
100
=
=
=
=
=
=
=
=
=
100
100
100
100
100
100
100
100
100
Lösung von Paula Petri, 8 Jahre, Klasse 3:
111 : 1 · 1 : 1 · 1 : 1 − 11
99 + 9 : 9 − 9 + 9 − 9 + 9 − 9 + 9
88 + 8 : 8 + 8 : 8 + 8 + [[8 + 8) : 8]
(222 − 22) : 2 − 2 + 2 − 2 + 2
(777 − 77) : 7 − 7 + 7 − 7 + 7
(666 − 66) : 6 − 6 + 6 − 6 + 6
(555 − 55) : 5 − 5 + 5 − 5 + 5
(444 − 44) : 4 − 4 + 4 − 4 + 4
(333 − 33) : 3 − 3 + 3 − 3 + 3
Lösung von Merle Duchene, 12 Jahre, Klasse 6:
100 kann man im Vierersystem mit 10 gleichen Ziffern schreiben:
11114 + 1114 − 114 − 14 = 6410 + 3210 + 410 = 10010
Lösung 85-42
8
Heike Winkelvoß, www.egladil.de
Man gibt dem einen Jungen 5 Stückchen, dem anderen 6 Stückchen. Dann
hat der eine nicht mehr bekommen als der andere, sondern weniger.
Lösung 85-43
Es seien x die Anzahl der Erwachsenen, y die Anzahl der Rentner und z
die Anzahl der Kinder. Dann gilt (ohne Maßeinheiten)
x + y + z = 30
2x + 1, 5y + z = 40
z = 2y
Schreibt man die linke Seite der zweiten Gleichung als (x + y + z) + x + 21 y,
so kann man die Summe in Klammern durch 30 ersetzen. Es gilt also
1
x + y = 10
2
Ersetzen wir in Gleichung 1 z durch 2y, so folgt
x + 3y = 30
Dies aufgelöst ergibt y = 8, also z = 16 und x = 6.
Das sind insgesamt 6 + 8 + 16 = 30 Personen, doppelt so viele Kinder (16)
wie Rentner (8) und sie bezahlten 6 · 2 e + 8 · 1, 5 e + 16 e = 40 e
Eintritt.
An dem Museumsbesuch nahmen 6 Erwachene, 8 Rentner und 16 Kinder
teil.
Lösung 85-44
35 Teiler, denn jede der Zahlen 30 , 31 , 32 , 33 , 34 , 35 , 36 kann mit jeder der
Zahlen 50 , 51 , 52 , 53 , 54 multipliziert werden. Das ergibt zusammen 5·7 = 35
Möglichkeiten.
Lösung 85-45
MATHE FÜR JUNG UND ALT - SERIE85 - JAN/FEB 2012
9
a) Die Differenz zwischen aufeinanderfolgenden Folgengliedern wird jeweils
verdoppelt. Daher heißt die fehlende Zahl 17 = 9 + 8.
b) Lösung von Frederike Jordan, 10 Jahre, Klasse 5: Die Zahlen
vergrößern sich im Wechsel um die nächsthöhere Potenz von 2 und
um die nächsthöhere Zahl beginnend mit der 4:
1, 5, 6, 11, 13, 19, 23, 30, 38
b) Lösung von Alexander Kiy, 8 Jahre, Klasse 4: ..., 12, 16, 17, 22, 23, 27, 28, 33,
(Immer im Wechsel +1, +4, +1, +5, +1, + 4, ...)
Lösung 85-46
Angenommen, der Junge ist x > 0 Jahre und 0 ≤ y < 12 Monate alt. Dann
gilt
12 · x + y − x = 11 · x + y = 111 = 11 · 10 + 1
Wegen y < 12 gilt y = 1 und x = 10. Der Junge ist am 14. Oktober 2005
also 10 Jahre und einen Monat alt. Das heißt, er hat am 14. September
1995 Geburtstag.
Lösung 85-47
Einige der vielen Möglichkeiten sind diese:
Oben links befinden sich jeweils die 4 einzelnen Lagen Papier (Faltung wie
in der Aufgabe):
10
Heike Winkelvoß, www.egladil.de
Lösung 85-48
5
Klassen 7 und 8
Lösung 85-51
Die 11 Kugeln bestehen zusammen aus 128 Masseeinheiten Gold, da sich
das Gewicht zweier Kugeln wie die dritte Potenz der Radien verhält:
5 · 1 + 4 · 23 + 1 · 33 + 1 · 43 = 5 + 32 + 27 + 64 = 64 + 64
Der eine Prinz bekommt die größte Kugel, der andere die ganzen kleineren.
MATHE FÜR JUNG UND ALT - SERIE85 - JAN/FEB 2012
11
Lösung 85-52
Wegen a > 2 und b > 2 gilt
1 1 1 1
+ < + =1
a b
2 2
Multipliziert man beide Seiten der Ungleichung mit ab > 0, erhält man
ab ab
+
< ab
a
b
a + b < ab
q.e.d.
Lösung 85-53
Aus z = 100a + 10b + c erhält man durch Einsetzen von a + b = c
z = 101a + 10b
Wegen a + b = b + a gibt es also halb so viele dreistellige Zahlen z, die die
Bedingungen erfüllen, wie es Möglichkeiten gibt, a und b zu wählen. Das
sind 90 : 2 = 45.
Lösung 85-54
Seien r der Inkreisradius und R der Umkreisradius, dann gilt nach Satz
des Pythagoras:
R2 = 2r2
Damit sieht man die Behauptung.
Lösung 85-55
12
Heike Winkelvoß, www.egladil.de
Es seien a > 0, b > 0 und c > 0 die Maßzahlen des Volumens des ersten,
zweiten bzw. dritten Behälters in Litern. Dann gilt nach Voraussetzung
a + b + c = 170
a − b − c = 10
2
b = a− a
9
Addition der beiden ersten Gleichungen ergibt a = 90, woraus mit der
dritten Gleichung b = 70 folgt. Für c muss dann c = 170 − 160 = 10 gelten.
Der erste Behälter fasst also 90 Liter, der zweite 70 Liter und der dritte 10
Liter.
Lösung 85-56
D
E
M
C
Wir beweisen, dass die Diagonale BD und die
Fünfeckseite AE parallel sind.
Es sei M der Mittelpunkt des Fünfecks
ABCDE. Aus der Tatsache, dass ABCDE
gleichseitig ist, folgen:
(1) 4AM D ∼
= 4BDM (Kongruenzsatz sws),
A
B
(2) 4AM D gleichschenklig mit | AM |=|
M D |,
(3) 4AM E gleichschenklig mit | ∠AM E |= 360◦ : 5 = 72◦ und
(4) | ∠AM B |= 2· | ∠ADB | (Peripherie-Zentriwinkelsatz im Umkreis
von ABCDE), also | ∠ADB |= 36◦ .
Aus (1) folgt, dass DM den Winkel ∠BDA halbiert. Es ist also zusammen
mit (4)
(5) | ∠M DA |=| ∠M AD |= 18◦ .
Aus (3) folgt
(6) | ∠M AE |= (180◦ − 72◦ ) : 2 = 54◦ (Innenwinkelsatz im Dreick
4AM E).
13
MATHE FÜR JUNG UND ALT - SERIE85 - JAN/FEB 2012
Nun ergibt sich aus (4), (5) und (6)
| ∠DAE |= 54◦ − 18◦ = 36◦ =| ∠BDA |
∠DAE und ∠BDA sind also gleich groß. Gleichzeitig sind beide Wechselwinkel bezüglich der von AD geschnittenen Strecken AE und BD. Daher
müssen AE und BD parallel sein, q.e.d.
Lösung 85-57
0.2
402
2012
403
2012
a) Wegen
0.4 <
402
403
805
+
=
≈ 0.4000994
2012 2012 2012
gilt
0.2 −
bzw
402
2012
402
403
<
− 0.2
2012 2012
−
Der Bruch
0.2
<
403
2012
−
0.2
402
2012
liegt also am nächsten an 0.2.
b) Wegen
1
1
= 0.3 und = 0.142857
3
7
hängt die 2012te Stelle der Summe nur von der 2012ten Stelle des zweiten
Summanden ab. Immer nach 6 Nachkommastellen wiederholen sich die
Ziffern. Nun gilt 335 · 6 = 2010. Nach 2010 Stellen beginnt also wieder die
Periode 142857. Die 2012te Stelle muss also die 4 sein. Da die 2013te Stelle
die 2 ist, gibt es bei der Addition von 1/3 keinen Übertrag. Die 2012te
Dezimalstelle von x ist folglich gleich 7.
Lösung 85-58
14
Heike Winkelvoß, www.egladil.de
Mai Nier. Otte Peters
Mai Nier. Otte Peters
Aach.
−
−
−
+
Hund
−
−
−
+(1)
Berl. +(1) −
Katze −(2) −(2) +
−
−(1)
−
Cottb. −
+
− −(1, 3) Wellens. +
−
−
−
Düss.
− −(2) +
−(2)
Meers. −(1) +
−
−
(1) ⇒ Herr Mai wohnt in Berlin und hat keinen Hund, Herr Peters hat
einen Hund und wohnt nicht in Berlin.
(1),(3) ⇒ Herr Peters und Herr Mai wohnen nicht in Düsseldorf und Herr
Mai hat kein Meerschweinchen.
(2) ⇒ Herr Mai hat keine Katze. Daher muss Herr Mai einen Wellensittich
haben.
hieraus und aus (1) und (2) ⇒ Herr Nierstein hat keine Katze, keinen Hund
und keinen Wellensittich und wohnt nicht in Berlin und nicht in Düsseldorf.
⇒ Herr Nierstein hat ein Meerschweinchen.
Damit und mit (3) ⇒ Herr Nierstein wohnt in Cottbus.
Herr Peters wohnt also nicht in Cottbus, Berlin oder Düsseldorf. Bleibt für
ihn nur noch Aachen.
Zusammenfassnd ergibt sich folgende Zuordnung:
Herr
Herr
Herr
Herr
6
Mai
Peters
Nierstein
Otte
Berlin
Aachen
Cottbus
Düsseldorf
Wellensittich
Hund
Meerschweinchen
Katze
Klassen 9 bis 13
Lösung 85-61
Lösung von Kim Holtze, 12 Jahre, Klasse 7:
Wenn es nur leichte und schwierige Aufgaben gibt, dann sind es 40 leichte
und 60 schwierige Aufgaben, also gibt es von den schwierigen 20 mehr als
von den leichten.
MATHE FÜR JUNG UND ALT - SERIE85 - JAN/FEB 2012
15
Begründung: 3 · 60 = 180; es sind aber nur 100 Aufgaben, 80 müssen also
mehrmals „gezählt“ worden sein. Das heißt für zwei Leute zu viel, also
80 : 2 = 40, das sind die leichten Aufgaben, die alle drei gelöst haben, also
auch nur einmal (statt dreimal) zur gesamten Anzahl der Aufgaben gezählt
werden dürfen.
Lösung 85-62
Es sei F der Flächeninhalt des Dreiecks 4ABC. Dann gilt
1
aha
F =
2
q
F = s(s − a)(s − b)(s − c)
(1)
(2)
Formel (2) ist die Heronische Dreiecksformel. Hieraus folgt
q
2 s(s − a)(s − b)(s − c)
ha =
a
Beweis der Ungleichung indirekt:
Angenommen, es gibt ein Dreieck, in dem
q
ha > s(s − a)
gilt. Dann ist
q
2 s(s − a)(s − b)(s − c) q
> s(s − a)
a
und damit
a2
(s − b)(s − c) >
4
1
Wegen s = 2 (a + b + c) ist das äquivalent mit [a − (b − c)] · [a + (b − c)] > a2
oder (binomische Formel)
a2 − (b − c)2 > a2
(3)
Wegen (b − c)2 > 0 ist (3) nicht möglich. Alle Umformungen waren äquivalent. Folglich kann die Annahme nicht wahr sein. Die behauptete Ungleichung gilt daher für jedes Dreieck ABC, q.e.d.
Lösung 85-63
16
Heike Winkelvoß, www.egladil.de
Multiplikation aller drei Gleichungen ergibt (xyz)2 = 16, woraus xyz = ±4
folgt. Mit Gleichung 1 schließen wir zunächst z = ±4 und dann x = ±2,
y = ±0.5. Unter Beachtung der Tatsache, dass x, y und z paarweise gleiche
Vorzeichen haben müssen (alle rechten Seiten sind positiv), erhalten wir
folgende Lösungen:
(2, 0.5, 4), (−2, −0.5, −4)
Lösung 85-64
Behauptung: Diese Gleichung hat keine Lösung mit ganzen Zahlen x, y, z.
Beweis (indirekt)
Zunächst halten wir fest, dass wir uns auf natürliche Zahlen x, y, z beschränken können, da auf der linken Seite der gegebenen Gleichung Quadrate stehen und somit eventuelle negative Vorzeichen verschwinden.
Angenommen, es gäbe natürliche Zahlen x, y, z, die die gegebene Gleichung
erfüllen. Da 2012 gerade ist, müssen dann entweder alle drei Summanden
x2 , y 2 , z 2 gerade sein oder genau zwei Summanden ungerade und der dritte
gerade.
Fall 1: Seien alle drei Summanden gerade.
Da das Quadrat einer geraden Zahl gerade, das Quadrat einer ungeraden
Zahl aber ungerade ist, gibt es in diesem Fall natürliche Zahlen a, b, c mit
x = 2a, y = 2b, z = 2c, woraus
x2 + y 2 + z 2 = 4(a2 + b2 + c2 ) = 2012
folgt, bzw.
a2 + b2 + c2 = 503
(1)
Nun ist die Summe dreier Zahlen genau dann ungerade, wenn entweder
alle Summanden ungerade sind oder genau ein Summand ungerade ist.
Fall 1.1: Seien a2 , b2 , c2 ungerade.
Mit einem analogen Schluss wie für x, y, z können wir im Fall a2 , b2 , c2
ungerade 3 natürliche Zahlen k, l, m finden, so dass a = 2k + 1, b = 2l +
1, c = 2m + 1 ist, bzw.
4k 2 +4k+1+4l2 +4l+1+4m2 +4m+1 = 4(k 2 +k+l2 +l+m2 +m)+3 = 503
MATHE FÜR JUNG UND ALT - SERIE85 - JAN/FEB 2012
17
also
k(k + 1) + l(l + 1) + m(m + 1) = 125
(2)
Auf der linken Seite von (2) steht eine Summe aus 3 Produkten je aufeinanderfolgender natürlicher Zahlen. Von 2 aufeinanderfolgenden natürlichen
Zahlen ist immer eine gerade, so dass jeder Summand auf der linken Seite
von (2) gerade ist. Dann kann die Summe aber nicht ungerade sein, so dass
(2) nicht mit natürlichen Zahlen lösbar ist. Die Zahlen a2 , b2 , c2 können also
nicht alle ungerade gewesen sein. Daher bleibt als einziger Fall (im Fall 1)
Fall 1.2: Seien a2 , b2 gerade, c2 ungerade.
Wir finden also natürliche Zahlen k, l, m so, dass a = 2k, b = 2l, c = 2m + 1
gilt. Aus (1) folgt damit
4k 2 + 4l2 + 4m2 + 4m + 1 = 4(k 2 + l2 + m2 + m) + 1 = 503
oder
4(k 2 + l2 + m2 + m) = 502
(3)
Auf der linken Seite von (3) steht eine durch 4 teilbare Zahl, rechts aber
nicht. (3) ist also nicht in N × N × N lösbar, d.h. auch Fall 1.2 hat uns zu
einem Widerspruch geführt.
Fall 1 ist vollständig untersucht und hat zu keiner Lösung der Kugelgleichung in N × N × N geführt.
Fall 2: Seien x2 , y 2 ungerade und z 2 gerade.
Dann finden wir natürliche Zahlen a, b, c, so dass x = 2a+1, y = 2b+1, z =
2c gilt. Damit folgt
4a2 + 4a + 1 + 4b2 + 4b + 1 + 4c2 = 4(k 2 + k + l2 + l + m2 + m) + 2 = 2012
oder
4(k 2 + k + l2 + l + m2 + m) = 2010
(4)
Der Term auf der linken Seite von (4) ist durch 4 teilbar, der auf der rechten
nicht. (4) ist damit in N × N × N nicht lösbar.
Unsere Fallunterscheidung ist vollstänig. Jeder betrachtete Fall hat zu einem Widerspruch geführt. Die Annahme kann daher nicht wahr gewesen
sein. Damit ist die Behauptung bewiesen. q.e.d.
Lösung 85-65
18
Heike Winkelvoß, www.egladil.de
Wegen
√
2012
2012
2012
ist
x=
√
2012
= 2012
2012
eine Lösung der gegebenen Gleichung. Weitere Lösungen kann es nicht
geben, da Potenzfunktionen mit positiven reellen Argumenten streng monoton wachsen.
Lösung 85-66
Setzt man Q(x) = P 2 (x) + 1 und R(x) = P (x2 + 1), so ist
1 = 1 + P 2 (0) = Q(0) = R(0) = P (1)
2 = 1 + P 2 (1) = Q(1) = R(1) = P (2)
5 = 1 + P 2 (2) = Q(2) = R(2) = P (5),
so dass man
n2 + 1 = Q(n) = R(n) = P (n2 + 1) für alle n ∈ N
vermutet. Um das Zutreffen dieser Vermutung zu beweisen, betrachte man
die durch
a0 = 0,
an+1 = a2n + 1 für alle n ∈ N
rekursiv definierte Folge. Dann ist
P (an ) = an
für alle n ∈ N,
(3)
wie nun durch vollständige Induktion über n gezeigt wird.
Induktionsanfang: P (a0 ) = P (0) = 0 gilt nach (2).
Induktionsschritt: Nach Definition von (an )n∈N und nach Induktionsvoraussetzung P (an ) = an , aus der sofort P 2 (an ) = a2n folgt, gilt
P (an+1 ) = P (a2n + 1) = R(an ) = Q(an )
= P 2 (an ) + 1 = a2n + 1 = an+1 .
Aus (3) ergibt sich nun das durch P (x) = x für alle reellen x definierte
Polynom P als das einzige, für das (1) und (2) erfüllt sind.
MATHE FÜR JUNG UND ALT - SERIE85 - JAN/FEB 2012
19