Aufgaben - Mathe für jung und alt

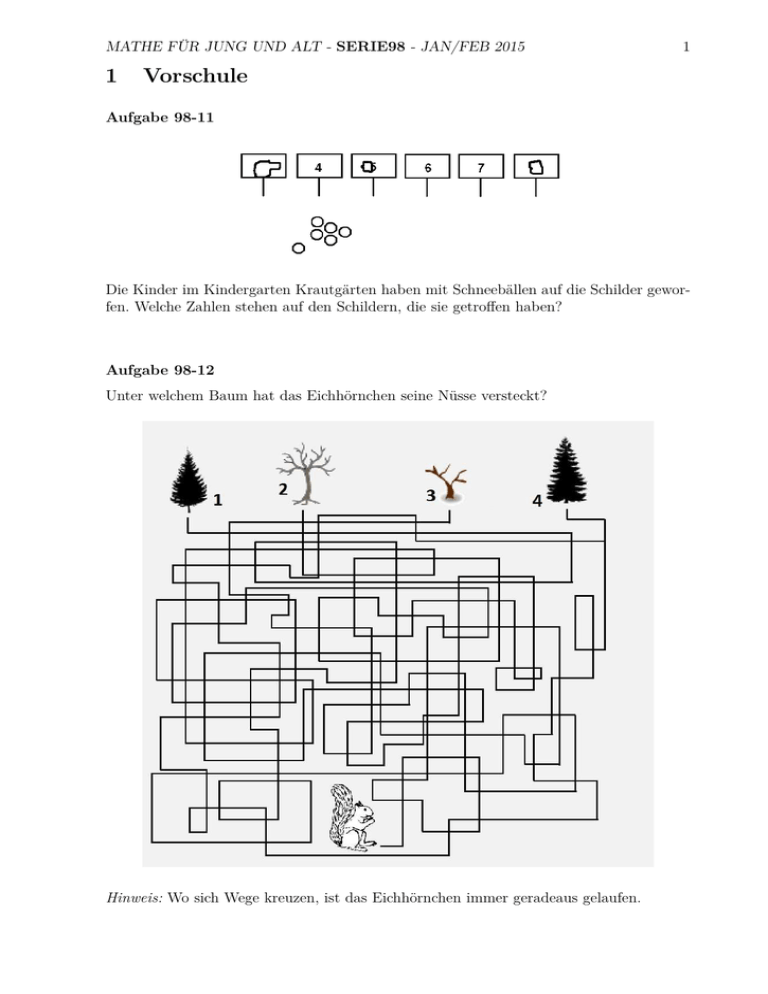
MATHE FÜR JUNG UND ALT - SERIE98 - JAN/FEB 2015
1
1
Vorschule
Aufgabe 98-11
Die Kinder im Kindergarten Krautgärten haben mit Schneebällen auf die Schilder geworfen. Welche Zahlen stehen auf den Schildern, die sie getroffen haben?
Aufgabe 98-12
Unter welchem Baum hat das Eichhörnchen seine Nüsse versteckt?
Hinweis: Wo sich Wege kreuzen, ist das Eichhörnchen immer geradeaus gelaufen.
2
Heike Winkelvoß, www.egladil.de
Aufgabe 98-13
Wie oft kann man mit diesen Ziffern die neue Jahreszahl 2015 legen?
Aufgabe 98-14
Heute ist Dienstag. In drei Tagen wird Julia mit ihrem Bruder Schlittschuh laufen gehen.
Am Tag darauf hat Julia Geburtstag.
An welchem Wochentag hat Julia Geburtstag?
2
Klassen 1 und 2
Aufgabe 98-21
Welches Profil hat der
Kradfahrer?
MATHE FÜR JUNG UND ALT - SERIE98 - JAN/FEB 2015
3
Aufgabe 98-22
Maria und Berenike, 10 Jahre, Klasse 4
Tom ist in einer Schwimmgruppe mit fünf anderen Kindern: Lara, Nina, Petra, Sabine
und Klaus. Heute ist Springen vom Drei-, Fünf- oder Zehnmeterturm auf dem Plan. Drei
Kinder springen vom Zehnmeterturm, zwei andere vom Fünfmeterturm und das sechste
vom Dreimeterturm. Lara traut sich, von einem höheren Turm zu springen als Nina. Nina
traut sich, von einem höheren Turm zu springen als Petra. Sabine springt von einem
höheren Turm als Klaus.
Welches Kind springt von welchem Turm?
Aufgabe 98-23
Maria und Berenike, 10 Jahre, Klasse 5:
Lisa wird 6 Jahre alt. Zu jedem Geburtstag bekommt sie 8 Legosteine. Zwei Wochen nach
ihrem Geburtstag hat ihre Freundin Lara Geburtstag. Ihre Mutter möchte, dass Lisa ihr
ein Viertel ihrer Legosteine schenkt.
a) Wie viele Legosteine hat Lisa an ihrem Geburtstag?
b) Wie viele Legosteine bekommt ihre Freundin?
c) Wie viele Legosteine hat Lisa nach Laras Geburtstag?
Aufgabe 98-24
Ina Menzerath, 10 Jahre, Klasse 5:
Ein Holz brennt 30 min. Wie lange brennen 12 Hölzer
der gleichen Größe, wenn man immer 2 zusammen anzündet und die nächsten zwei erst, wenn die vorigen erloschen sind?
Aufgabe 98-25
Ersetze die Punkte . . . durch Plus- und Minuszeichen, so dass alle Aufgaben richtig gerechnet sind:
36 . . . 33 . . . 5 = 8
52 . . . 13 . . . 38 = 27
12 . . . 5 . . . 40 = 57
90 . . . 20 . . . 30 = 80
4
Heike Winkelvoß, www.egladil.de
Aufgabe 98-26
Linus möchte mit dem Bus zur Schmiedestraße fahren. Er kommt zehn Minuten vor halb
drei an der Haltestelle Schlackenplatz an und nimmt den nächstmöglichen Bus. Zum Glück
fährt dieser pünktlich ab. Wie lange hat Linus gewartet?
Aufgabe 98-27
In Runde 12 hatten Kinder die Aufgabe, Kreuzgitter zu erfinden. Diese Aufgabe ist daraus
entstanden:
Trage die fehlenden Zahlen so ein, dass alle Gleichungen von links nach rechts und von
oben nach unten stimmen. Dabei sollst du immer alle angegebenen Zahlen verwenden.
Deshalb stehen manche Zahlen mehrmals da.
a) Chiara:
b) Amelie Sophie:
1, 2, 3, 4, 5, 5, 7, 9, 12
=
+
+
+
+
=
+
−
+
=
+
=
−
=
=
=
+
=
+
=
1, 1, 2, 4, 6, 6, 7, 11, 12
=
+
=
=
5
MATHE FÜR JUNG UND ALT - SERIE98 - JAN/FEB 2015
c) Johannes:
d) Platz für ein eigenes Kreuzgitter:
4, 5, 5, 6, 9, 15, 15, 20
=
=
+
−
+
+
=
=
−
=
=
=
=
=
=
=
+
=
Aufgabe 98-28
Auf dem Schulfest hat die Klasse 2 insgesamt 61 Euro eingenommen. Für die Faschingsfeier
sollen davon Getränke und Berliner gekauft werden. Eine Schachtel mit 10 Berlinern
kostet 10 Euro. Eine Kiste Getränke kostet 7 Euro. Wie viele Kisten Getränke können
noch gekauft werden, wenn 40 Berliner gekauft werden sollen?
3
Klassen 3 und 4
Aufgabe 98-31
Rechne folgende Aufgaben. Beachte dabei die Regel
Punktrechnung geht vor Strichrechnung:
also mit · und : beginnen, dann erst + und − rechnen.
a) 97 − 4 · 8 + 20 =
c) 64 : 8 + 92 − 100 =
b) 9 : 9 + 4 · 4 =
d) 33 + 32 − 7 · 9 =
Aufgabe 98-32
Lars hat mit genau einem Wurf die Augenzahl
a) 7
b) 13
gewürfelt. Wie viele Spielwürfel hat er dabei mindestens benutzt und wie viele
höchstens? Welche Augenzahlen zeigten die Würfel dabei?
6
Heike Winkelvoß, www.egladil.de
Aufgabe 98-33
Anna, Sarah und Lucy sind begeisterte Leseratten. Jede liest gerade ein anderes der
Bücher „Eragon“ , „Harry Potter“ und „Krabat“ . Es ist Folgendes bekannt:
(a) Sarah und das Mädchen, das „Krabat“ liest, gehen in dieselbe Klasse.
(b) Das Mädchen, das „Eragon“ liest, und Anna kennen Lucys Buch schon.
(c) Lucys und Sarahs Klasse waren im vergangenen Schuljahr gemeinsam im Schullandheim.
Welches Mädchen liest welches der Bücher? Begründe!
Aufgabe 98-34
Ein Rechteck hat die Seitenlänge | AB |=40 cm und | BC |=30 cm.
Wie lang ist die Seitenlänge eines Quadrates, das den selben Umfang hat wie das Rechteck?
Aufgabe 98-35
Streiche in der Zahl 3728954106 genau drei Ziffern, so dass die verbleibenden Ziffern in
der bestehenden Reihenfolge die kleinstmögliche Zahl bilden. Welche Ziffern streichst du
und wie lautet die kleinstmögliche Zahl?
Aufgabe 98-36
Um meinen grünen Tee zuzubereiten, bringe ich 1 Liter Wasser zum Kochen und fülle dieses mit Leitungswasser zu 1,5 Liter auf. Diesmal habe
ich nur 500 Milliliter Wasser zum Kochen gebracht. Wieviel Leitungswasser muss ich hinzufügen damit das Wasser zum Aufbrühen des Tees
die gleiche Temperatur hat wie sonst?
Aufgabe 98-37
Primzahlen sind Zahlen, die durch genau 2 Zahlen teilbar sind, also nicht durch mehr und
nicht durch weniger als 2 Zahlen.
a) Welches ist die kleinste Primzahl?
b) Ist 1 eine Primzahl? Bitte begründe deine Antwort.
c) Wie viele Primzahlen zwischen 1 und 20 gibt es? Schreibe sie auf.
d) Welches ist die größte zweistellige Primzahl?
MATHE FÜR JUNG UND ALT - SERIE98 - JAN/FEB 2015
7
Aufgabe 98-38
2015 kann als Summe von 5 aufeinanderfolgenden Zahlen geschrieben werden. Wie lautet
der kleinste Summand?
4
Klassen 5 und 6
Aufgabe 98-41
Von einem Quadrat wurden, wie auf dem Bild ersichtlich, rechtwinklige Dreiecke abgeschnitten. Welchen Flächeninhalt hat das übrig gebliebene Flächenstück, das grau dargestellt wurde?
Aufgabe 98-42
Alexander schläft täglich 1/3 seiner Zeit, 1/4 verbringt er in der Schule, 1/6 liest er, 1/8
spielt er Fußball, 1/10 schreibt er und 1/12 isst er und 1/24 hilft er im Haushalt.
Ist das möglich?
Aufgabe 98-43
Leo Gitin, 8 Jahre, Klasse 3:
In dieser Additionsmauer ergibt sich die Zahl in jedem Stein ab Ebene 2 aus der Summe
der Zahlen in den beiden darunter liegenden Steinen.
Welche Zahl steht anstelledes Fragezeichens?
8
Heike Winkelvoß, www.egladil.de
Aufgabe 98-44
Finde alle dreistelligen durch 3 teilbaren natürlichen Zahlen, die auf 3 enden.
Aufgabe 98-45
Herr Müller hat eine einzigartige Sammlung von Gewichten zu 1g, 2g, . . ., 100g, 101g.
Das 19-Gramm-Gewicht hat er seiner Enkelin zum Spielen gegeben. Jetzt möchte er die
verbliebenen Gewichte alle so auf seine Balkenwaage legen, dass diese anschließend im
Gleichgewicht ist.
Kann er das schaffen? Wenn ja, wie macht er es? Wenn nicht, warum?
Aufgabe 98-46
Trage alle Ziffern 0, 1, 2, . . . , 8, 9 so in die leeren Felder ein, dass beide Gleichungen stimmen:
Aufgabe 98-47
Primzahlen sind Zahlen, die genau zwei Teiler haben. 2 ist die kleinste Primzahl - sie hat
die Teiler 1 und 2. 4 ist keine Primzahl, denn sie hat die 3 Teiler 1, 2 und 4.
Der Mathematiker Christian Goldbach (1690- 1764) hat folgende Vermutung ausgesprochen:
Jede gerade Zahl, die größer als 2 ist, lässt sich als Summe zweier Primzahlen
darstellen.
Zum Beispiel ist 6 = 3 + 3 oder 18 = 7 + 11. Die Goldbachsche Vermutung ist bis heute
(20.07.2014) noch nicht bewiesen.
Überprüfe die Vermutung für alle geraden Zahlen, die kleiner als 50 sind.
Aufgabe 98-48
Auf wie viele Weisen kann man 2015 als Produkt von genau 2 verschiedenen Faktoren
schreiben? 1 ist als Faktor erlaubt.
MATHE FÜR JUNG UND ALT - SERIE98 - JAN/FEB 2015
5
9
Klassen 7 und 8
Aufgabe 98-51
Zähler und Nenner einer rationalen Zahl seien positive ganze Zahlen deren Summe gleich
101 sei. Ferner ist bekannt, dass der Bruch nicht größer als 31 sei.
Finde die größtmögliche Zahl, die diesen Bedingungengenügt.
Aufgabe 98-52
Man zeige, dass für beliebiges n ∈ N die Zahl n5 − 5n3 + 4n durch 120 teilbar ist.
Aufgabe 98-53
In einem Kreis k wurde zwei verschieden lange Sehnen AB und CD, die sich im Punkt S schneiden,
eingezeichnet. Die Endpunkte dieser Sehnen erzeugen, wie aus dem Bild ersichtlich, vier Kreisbögen
der Länge b1 , b2 , b3 bzw. b4 . Es ist zu beweisen: Wenn
b1 + b2 = b3 + b4 , dann stehen AB und CD senkrecht
aufeinander.
Zusatz: Gilt auch die Umkehrung?
Aufgabe 98-54
Zeige, dass
2009 · 2011 · 2013 · 2015 + 16
eine Quadratzahl ist.
Selbstverständlich sind Taschenrechner oder Computer nicht erlaubt.
Aufgabe 98-55
Finde und beweise eine Formel, mit der du die Anzahl der Diagonalen in einem konvexen
n-Eck berechnen kannst. Welches konvexe n-Eck hat genau 2015 Diagonalen?
10
Heike Winkelvoß, www.egladil.de
Aufgabe 98-56
Von einer Sorte Orangen in unserem Supermarkt haben alle Früchte einen Durchmesser
von 12 cm und eine 1 cm dicke Schale. Bei einer Sorte Mandarinen sind Durchmesser und
Schale jeweils genau halb so dick. (Wir nehmen an, dass alle Orangen und alle Mandarinen
exakt gleich große Kugeln seien und die Schale ebenfalls überall gleich dick.)
Wie viele Mandarinen müsste ich mindestens kaufen, damit ich nicht weniger Frucht
bekomme als bei einer Orange?
6
Klassen 9 bis 13
Aufgabe 98-61
Berechne die Summe
1
1
1
1
1
+
+
+ ··· +
+
1·3 3·5 5·7
2011 · 2013 2013 · 2015
Aufgabe 98-62
Zwei verschiedene natürliche Zahlen bezeichnen wir als GUTE, wenn diese sich in dieselben Primzahlen zerlegen lassen (im allgemeinen mit verschiedenen Potenzen, z.B. 30 =
2 · 3 · 5 und 3000 = 23 · 3 · 53 ).
Diese Zahlen heißen dann SEHR GUTE, wenn die beiden nächsten natürlichen Zahlen
auch GUT sind (z.B. 6 = 2 · 3 und 48 = 24 · 3 sind SEHR GUT, weil 6 + 1 = 7 und
48 + 1 = 49 = 72 auch GUT sind).
Ist die Anzahl der SEHR GUTEN Zahlenpaare endlich oder unendlich?
Aufgabe 98-63
U. Willrett:
Die Dezimaldarstellung einer Zahl Z besteht aus je einer Eins am Anfang und am Ende,
dazwischen stehen 2012 Nullen: 1000 · · · 01, d.h. die Zahl hat 2014 Ziffern.
Ist Z eine Primzahl?
11
MATHE FÜR JUNG UND ALT - SERIE98 - JAN/FEB 2015
Aufgabe 98-64
Der Term
q
√
99 + 70 2 −
q
√
99 − 70 2
ist so weit wie möglich zu vereinfachen.
Aufgabe 98-65
Es ist nachzuweisen, dass
47 > 56 > 65 > 74 > 83 > 92 > 101
ist.
Aufgabe 98-66
U.Warnecke, Münster:
a) Gegeben sei ein Parallelogramm ABCD mit den Seitenlängen a, b, c und d und den Diagonallängen e
und f (vgl. Fig.). Beweise: a2 +b2 +c2 +d2 = e2 +f 2 .
D
b) Versuche, eine entsprechende Formel für beliebige
Vierecke zu finden. Ziehe dazu die Diagonalenmittelpunkte mit in Betracht.
Bemerkung: Von einem der genialsten und bedeutendsten Mathematiker wurde eine solche Formel gefunden.
Weißt du, welcher Mathematiker damit gemeint ist?
d
c
e
C
b
f
α
A
a
B
12
Heike Winkelvoß, www.egladil.de
Quellennachweis:
Aufgabe 98-21: Leipziger Volkszeitung(1)1983
Aufgabe 98-22: Ina Menzerath, 10 Jahre, Klasse 5
Aufgabe 98-23: Berenike Buervenich, 9 Jahre, Klasse 5
Aufgabe 98-24: Ina Menzerath, 10 Jahre, Klasse 5
Aufgabe 98-27: Amelie-Sophie Hilkinger, Chiara Franz, Johannes Valk
Aufgabe 98-34: alpha(6)1986
Aufgabe 98-35: Moskauer Mathematikolympiade(2051)2001
Aufgabe 98-41: alpha(2)1984
Aufgabe 98-43: Leo Gitin, 8 Jahre, Klasse 3
Aufgabe 98-46: alpha(4)1984
Aufgabe 98-51: Mathefest (Russland)(7)1999
Aufgabe 98-53: alpha(1)1982
Aufgabe 98-62: alpha(5)1977
Aufgabe 98-63: Ursel Willrett
Aufgabe 98-64: alpha(1)1986
Aufgabe 98-65: alpha(1)1987
Aufgabe 98-66: Ulrich Warnecke
Rest: Heike Winkelvoß