Anwendung v. Faltungstheorem: Tiefpassfilter Wähle so, dass falls

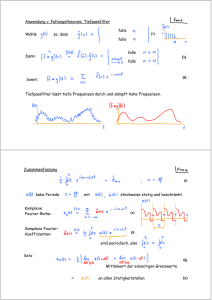
Anwendung v. Faltungstheorem: Tiefpassfilter
Wähle
falls
so, dass
falls
falls
Dann:
falls
Somit:
Tiefpassfilter lässt tiefe Frequenzen durch und dämpft hohe Frequenzen.
Zusammenfassung
habe Periode
, mit
stückweise stetig und beschränkt.
Komplexe
Fourier-Reihe:
Komplexe FourierKoeffizienten:
sind periodisch, also
Satz
Mittelwert der einseitigen Grenzwerte
an allen Stetigkeitstellen
Reelle Fourier-Reihe:
Reelle FourierKoeffizienten:
Parseval-Identität:
Definition: Faltung
Faltungstheorem:
Differenzieren:
Fourier-Koeffizienten der Ableitung
Fourier-Reihe einer Ableitung:
Ist dieses konsistent mit (2) ?
Check:
partielle
Integration
Zur Erinnerung: Partielle Integration (ganz allgemein)
Beispiel: Gedämpfter HO mit periodischem (nicht-harmonischem) Antrieb
Gedämpfter HO:
Periodischer
Antrieb:
Suche partikuläre Lösung,
mit periodischem Ansatz:
(3), (2) in (1):
(5) gilt für alle t. Nur möglich, falls
DGL wird im Fourier-Raum zu einer algebraischen Gleichung! (Gewaltige Vereinfachung!)
Ferner: Faltungsth.
rückwärts gelesen impliziert:
9.2 Dirac -
Funktion:
mit
(Hilfsmittel zur Beschreibung scharfer Peaks)
ist ein unendlich hoher, infinitesimal scharfer Peak bei t = 0 :
Werte:
Normierung:
für
für
falls
Aufzufassen als Limes einer Folge immer schärferer, normierter Peaks.
Beispiele:
Rechtecke:
Dreiecke:
Lorentz-Peaks:
Exp.-Peaks:
Fläche
Fläche
Wird
für sich allein betrachtet, existiert der Limes nicht, denn
Allerdings ist der Limes wohldefiniert, wenn
unter einem (verallgemeinerten)
Integral vorkommt, für das die Konvention festgelegt wird, das
Integral zu berechnen, bevor der Limes gebildet wird.
z.B. für
(18.3):
Weil
nur im Bereich
können wir im im Limes
ersetzen! Annahme dabei: bei
Gewicht hat,
unter dem Integral
ist
hinreichend glatt.
ist eine "verallgemeinerte Funktion" oder "Distribution",
(definiert über Folgen), d.h. eine Abbildung einer Funktion auf eine Zahl:
Definition:
Beispiel 1: Anwendung von
in der Physik:
ist mathematische Idealisierung eines Pulses, dessen Zeitdauer kleiner ist als
alle Zeitskalen des Problems.
"Stärke des Pulses" normiert:
Physikalische Dimension:
Beispiel: Kraftpuls
Dimensionen:
Kraft = Impuls pro Zeit
Gesamtimpulsübertrag:
Anwendung:
Antwort eines gedämpften HO auf delta-Puls:
[Faltung von Inhomogenität ( = Puls)
mit Antwortfunktion]
Beispiel 2: Anwendung von
in der Physik
3-dimensionale deltaFunktion der Position:
mit
(Länge)
Dimension:
Ladungsdichte einer "Punktladung"
bei
(Volumen)
:
(mathematische Idealisierung einer Ladungsverteilung, deren Ausdehnung
kleiner ist als anderen Lägenskalen des Problems)
Gesamtladung:
Potential einer
Punktladung:
Eigenschaften der delta-Funktion:
[Annahme: f(t) ist hinreichend glatt!]
(können im Rahmen der "Distributionstheorie" (L. Schwartz) sauber bewiesen werden)
falls
ansonsten
für alle stetigen oder differenzierbaren Funktionen
Beispiel:
Konsequenz v. 1:
Insbesondere:
Aber: Produktbildung mit singulären Funktionen, insbesondere
(eine gerade Funktion)
denn:
, ist nicht möglich!
für
denn:
wobei
die einfachen
Nullstellen von
sind
(Verallgemeinerung von 4.)
falls
falls
Ableitung der delta-Funktion,
wird definiert durch:
(zu zeigen via partieller Integration)
Periodische delta-Funktion:
Betrachte:
Behauptung: die entsprechende Fourier-Reihe hat die Form
d.h., die Fourier-Koeffizienten sind n-unabhängig (!) :
Zunächst Plausibilitätsargument:
Periodisch:
denn
Divergiert bei 0
Verschwindet ansonsten:
Geometrisches Argument: deckt ganzen Einheitskreis ein, Vektorsumme =
Gewicht in
einer Periode:
.
Herleitungen von
:
(eine von vielen möglichen... )
Strategie: Konstruiere eine periodische Kette von delta-artigen Pulsen,
jeder mit Höhe
Breite
, und normiertem Gewicht
.
Berechne Fourier-Koeffizienten der Kette, und nehme am Ende den Limes
Periodische Kette:
normierter
"Exponentialpuls":
falls
falls
Gewicht:
"unendlich hoher",
"unendlich scharfer"
Peak, Gewicht 1 !!
Beispiel einer
"delta-Funktion":
Also:
Fourier-Koeffizienten von
:
falls
(scharfe Pulse, gut getrennt)
dann gilt im Interval
:
wenn
komplex
konjugiert
Limes
"Diskretes
Frequenzspektrum"
("Frequenzkamm")
mit Lorenzkurve
als Einhüllenden
:
unabhängig von n !
Bemerkung:
Für
vergleiche Schärfe der Pulse in
Zeitdarstellung:
Frequenzdarstellung:
Zeitlich scharfe Pulse (
klein)
haben ein breites "Frequenzspektrum" (
Faustregel:
Heisenbergs Unschärferelation in der
Quantenmechanik ist von ähnlicher Natur!
(und zu Grunde liegende Mathematik ist auch dort Fourier-Analysis! )
Periodische delta-Funktion erlaubt uns einen Konsistenzcheck für
Fourier-Reihendarstellung von period. Funktionen:
konsistent?
Vertausche Summe und Integral (Konvergenz vorausgesetzt)
periodisch:
denn
denn
ist periodisch!
sei so gewählt, dass
groß)
Zusammenfassung : Fourier-Reihen
Theorem : Jede (nicht-pathologische) periodische Funktion
läßt sich schreiben als "Fourier-Reihe" der Form:
Vorzeichen ist Konvention, in Mathe : +
Fourier-Transformation
mit FourierKoeffizienten :
Fourier-Rücktransformation
Wichtige Eigenschaften der Fourier-Exponenten
:
"Orthonormalität" :
"Vollständigkeit" :
Mathematischer Hintergrund: "Orthogonale Funktionen"
Theorem:
sei ein abzählbar unendlicher Satz von
komplexen Funktionen auf dem Interval
mit folgenden Eigenschaften :
"Orthonormalität" :
"Vollständigkeit" :
Dann läßt sich jede (nicht-pathologische) Funktion f(t) auf I darstellen als:
wobei Koeffizienten
gegeben sind durch:
D.h. die Funktionen
bilden eine Basis im Vektorraum aller Funktionen f(t) auf I.
Konsistenzcheck 1:
(3) in (4) :
Konsistenzcheck 2 :
(4) in (3) :
Fourier-Fktn.
sind orth. Fktn. mit periodischen Randbedingungen :
dann
Sei
Orthonormalität:
Vollständigkeit:
für
Fazit: Fourier-Entwicklungsatz (14.2), (14.3) ein Spezialfall (für periodische
Randbedingungen) von Theorem von (30.3), (30.4) !