Fourier-Reihen für periodische Funktionen Sei periodisch, mit
Werbung

Fourier-Reihen für periodische Funktionen
periodisch, mit Periode L:
Sei
Auch für diesen Fall gilt die FourierReihen-Darstellung (b.3), mit
(und stückweise stetig differenzierbar)
:
(b.3)
(c.5)
Integral kann über eine beliebige Periode genommen
Beweis v. (3): identisch zur Herleitung auf Seite C6.1c
werden, wegen (1) und (5)
Begründung:
Fourier-Moden
sind periodisch:
Folglich ist auch
(2) periodisch:
Periodische
delta-Funktion:
[vergleiche (j.2)]
Anmerkung: Falls f(x) nicht ganz glatt ist, sondern nur stückweise stetig
differenzierbar ist (d.h. Sprünge hat), gilt (Satz v. Dirichlet):
Die Fourier-Reihe (l.2),
, konvergiert
an allen Stetigkeitstellen gegen
.
An den Unstetigkeitstellen ist der Wert der
Fourier-Reihe gleich dem Mittelwert
der einseitigen Grenzwerte:
Grund für (1): [vergleiche (g.1)]:
Beispiel: periodische Folge v. scharfen Peaks:
Betrachte normierten
'Exponentialpuls':
Gewicht:
Periodische Kette
solcher Peaks:
Berechne Fourier-Koeffizienten von
, für
:
weil
(scharfe Pulse, gut getrennt)
gilt im Interval
dass
komplex
konjugiert
wenn
komplex
konjugiert
'Diskretes Frequenzspektrum'
('Frequenzkamm') mit
Lorenzkurve als Einhüllenden
Konsistenzcheck:
Im Limes
(5) reproduziert die
Fourier-Komponenten
vom delta-Puls:
:
(C6.2b.6)
unabhängig von k !
= konsistent mit (5)
Bemerkung:
Für
vergleiche Schärfe der Pulse in
x-Darstellung:
k-Darstellung:
Faustregel:
'Fourier-Gegensätzlichkeit'
('Fourier repricosity')
Räumlich scharfe Pulse (
klein) haben ein breites
'Spektrum an Wellenlängen' ( groß)
Heisenbergs Unschärferelation in der
Quantenmechanik ist ganz analog:
(und zu Grunde liegende Mathematik ist auch dort Fourier-Analysis! )
Faltungstheorem:
Seien
periodische Funktionen,
dann ist die Faltung
wieder periodisch:
Beweis: via Fourier-Darstellung der Faltung: [Details sind analog zu Seite k, Parseval]
(kühnes Vertauschen
von Integral und Summe)
= offensichtlich
wieder periodisch!
Fourierkoeffizient der Faltung ist
Produkt der Fourierkoeffizienten!
(nützlich zur Abkürzung von Rechnungen)
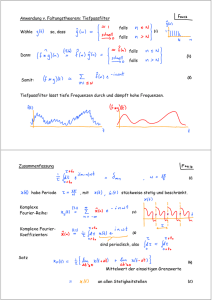
Anwendung v. Faltungstheorem: Tiefpassfilter
Wähle
falls
so, dass
falls
falls
Dann:
falls
Somit:
Tiefpassfilter dämpft schnelle Flutkuationen weg, läßt langsame durch !
Fourier-Reihe einer Ableitung:
Fourier-Komponente von f'(x)
Ist (4) konsistent mit (2) ?
Check:
partielle
Integration
Fazit: Ableiten in x-Darstellung
wegen Periodizität
Multiplikation mit
in k-Darstellung
Cosinus- und Sinus-Reihen (erhalten durch Umschreiben d. Fourier-Reihe)
oft nutzt man hier auch die
Notation
und
wobei
Cos, Sin-Reihen sind nützlich, falls f(x) symmetrisch oder antisymmetrisch ist:
Dann wird Berechnung der Fourier-Komponenten erheblich vereinfacht,
wenn das Integrationsinterval symmetrisch um x=0 gewählt wird:
Falls f symmetrisch, mit
Falls f antisymmetrisch, mit
Beispiel: Periodische Rechtecksfunktion
falls
falls
falls
"Vorzeichenfunktion"
für
und
Fourier-Koeffizienten:
Reine Sinus-Reihe, da
für beliebige
"periodische
Fortsetzung"
falls n gerade
falls n ungerade
periodisches
Für
liefert (6):
Mittelwert
siehe (m.1)]
Anmerkung zu Notationskonventionen
Warnung: es gibt in der Literatur viele unterschiedliche Konventionen!
Vorzeichen von k im
Exponenten ist Konvention:
Alternativ wäre
auch möglich:
Auch der Vorfaktor
L kann anders gewählt
werden; z.B.:
Oder auch:
In Physik-Anwendungen, wo Funktion von der Zeit abhängt, wird die FourierTransformation von Zeit-Darstellung zu Frequenz-Darstellung meist wie folgt definiert:
Für
anderes Vorzeichen als bei xk-Darstellung (1) !
Fourier-ReihenAnsatz:
Zusammenfassung C6.1 Fourier-Reihen für periodische Funktionen
periodisch, mit Periode L:
Sei
(b.3)
(c.5)
beliebige Periode
Faltung:
Ableitung in Fourier-Darstellung:
Zeit-Darstellung:
Für
Fourier-ReihenAnsatz:
Ableitung:

![Hypokaliämische Periodische Paralyse (HypoPP) [G72.3]](http://s1.studylibde.com/store/data/001720299_1-84537373347b5e29a0881fc5a3cfbe49-300x300.png)