( ) ∫ ∫ I ∫ I ∫ ∫ ∫
Werbung
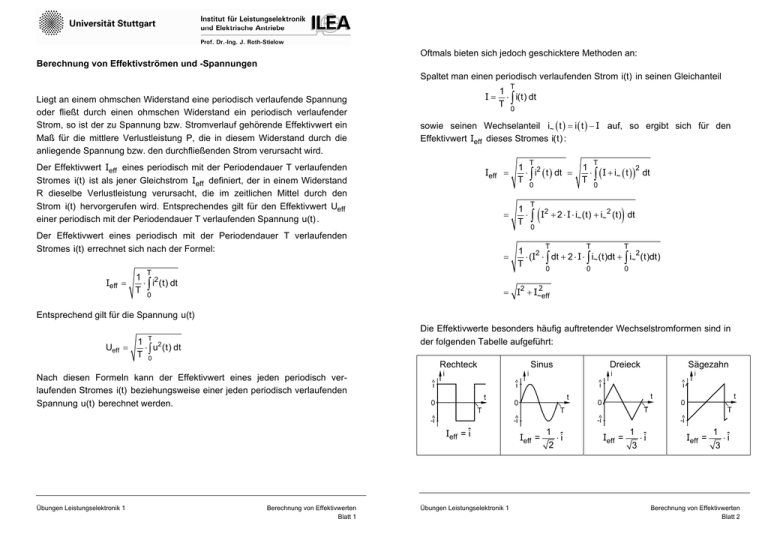
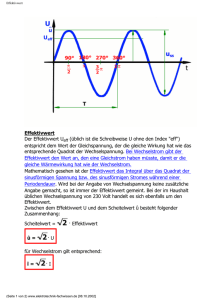
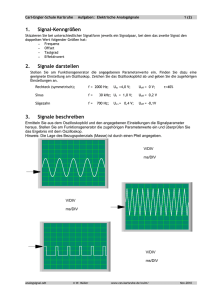
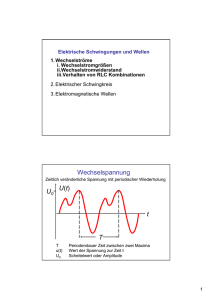
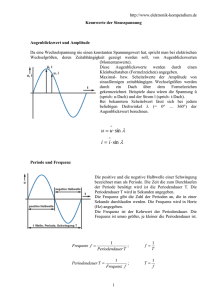
Oftmals bieten sich jedoch geschicktere Methoden an: Berechnung von Effektivströmen und -Spannungen Spaltet man einen periodisch verlaufenden Strom i(t) in seinen Gleichanteil T Liegt an einem ohmschen Widerstand eine periodisch verlaufende Spannung oder fließt durch einen ohmschen Widerstand ein periodisch verlaufender Strom, so ist der zu Spannung bzw. Stromverlauf gehörende Effektivwert ein Maß für die mittlere Verlustleistung P, die in diesem Widerstand durch die anliegende Spannung bzw. den durchfließenden Strom verursacht wird. I= 1 ⋅ i(t) dt T ∫ 0 sowie seinen Wechselanteil i~ ( t ) = i ( t ) − I auf, so ergibt sich für den Effektivwert Ieff dieses Stromes i(t) : T Der Effektivwert Ieff eines periodisch mit der Periodendauer T verlaufenden Stromes i(t) ist als jener Gleichstrom Ieff definiert, der in einem Widerstand R dieselbe Verlustleistung verursacht, die im zeitlichen Mittel durch den Strom i(t) hervorgerufen wird. Entsprechendes gilt für den Effektivwert Ueff einer periodisch mit der Periodendauer T verlaufenden Spannung u(t) . Ieff = 1 2 ⋅ i ( t ) dt = T ∫ 0 = Der Effektivwert eines periodisch mit der Periodendauer T verlaufenden Stromes i(t) errechnet sich nach der Formel: = 1 ⋅ T ∫ (I 2 ) + 2 ⋅ I ⋅ i~ (t) + i~2 (t) dt 0 T T T 0 0 0 1 2 ⋅ (I ⋅ ∫ dt + 2 ⋅ I ⋅ ∫ i~ (t)dt + ∫ i~2 (t)dt) T = I2 + I 2 f f e ~ Ieff = 0 T T 1 2 ⋅ i (t) dt T ∫ T 1 2 ⋅ ∫ ( I + i~ ( t ) ) dt T 0 Entsprechend gilt für die Spannung u(t) Ueff = Die Effektivwerte besonders häufig auftretender Wechselstromformen sind in der folgenden Tabelle aufgeführt: T 1 ⋅ ∫ u2 (t) dt T 0 Rechteck Sinus Dreieck Sägezahn Nach diesen Formeln kann der Effektivwert eines jeden periodisch verlaufenden Stromes i(t) beziehungsweise einer jeden periodisch verlaufenden Spannung u(t) berechnet werden. Übungen Leistungselektronik 1 I f f e ˆ i 1 2 = Berechnung von Effektivwerten Blatt 1 i = Übungen Leistungselektronik 1 f f e I ⋅ˆ Ieff = 1 ˆ ⋅i 3 Ieff = 1 ˆ ⋅i 3 Berechnung von Effektivwerten Blatt 2