Kennwerte der Sinusspannung

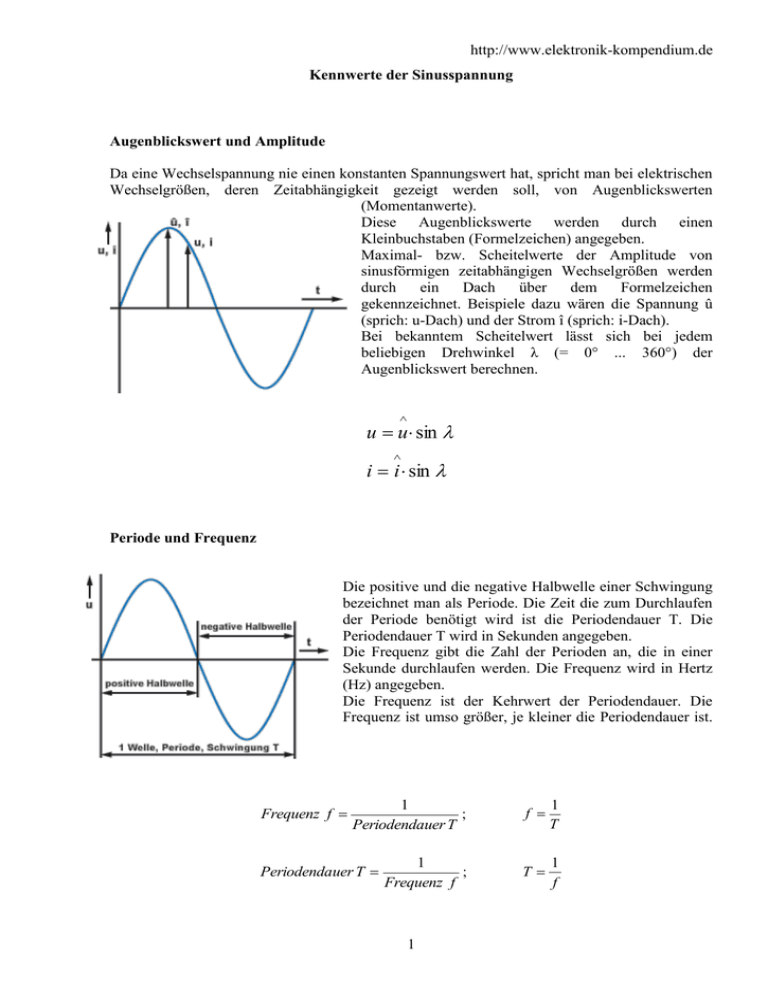
http://www.elektronik-kompendium.de
Kennwerte der Sinusspannung
Augenblickswert und Amplitude
Da eine Wechselspannung nie einen konstanten Spannungswert hat, spricht man bei elektrischen
Wechselgrößen, deren Zeitabhängigkeit gezeigt werden soll, von Augenblickswerten
(Momentanwerte).
Diese Augenblickswerte werden durch einen
Kleinbuchstaben (Formelzeichen) angegeben.
Maximal- bzw. Scheitelwerte der Amplitude von
sinusförmigen zeitabhängigen Wechselgrößen werden
durch
ein
Dach
über
dem
Formelzeichen
gekennzeichnet. Beispiele dazu wären die Spannung û
(sprich: u-Dach) und der Strom î (sprich: i-Dach).
Bei bekanntem Scheitelwert lässt sich bei jedem
beliebigen Drehwinkel λ (= 0° ... 360°) der
Augenblickswert berechnen.

u  u sin 

i  i  sin 
Periode und Frequenz
Die positive und die negative Halbwelle einer Schwingung
bezeichnet man als Periode. Die Zeit die zum Durchlaufen
der Periode benötigt wird ist die Periodendauer Τ. Die
Periodendauer Τ wird in Sekunden angegeben.
Die Frequenz gibt die Zahl der Perioden an, die in einer
Sekunde durchlaufen werden. Die Frequenz wird in Hertz
(Hz) angegeben.
Die Frequenz ist der Kehrwert der Periodendauer. Die
Frequenz ist umso größer, je kleiner die Periodendauer ist.
Frequenz f 
1
;
Periodendauer T
f 
1
T
1
;
Frequenz f
T
1
f
Periodendauer T 
1
http://www.elektronik-kompendium.de
Kennwerte einer Sinuskurve
Formelzeichen
ûss
Beschreibung
Formel

Die Spitze-Spitze-Spannung ûss liegt zwischen dem
positiven und negativen Spitzenwert einer Periodendauer.

u ss  2  u s

u ss  2  u eff  2
2  1.414
ûs
Die Spitze-Spannung ûs ist das positive oder das negative
Maximum einer Halbwelle.

u s  u eff  2
2  1.414
ueff
Der Effektivwert ueff ist ca. 70,7% der Spitze-Spannung ûs.
Wechselspannungswerte werden in der Regel als
Effektivwert angegeben.
Der Effektivwert gibt an, welcher Gleichstrom dieselbe
Leistung hat.

u eff  u s 
1
2
1
 0.707
2
T
Die Periodendauer T ist die Dauer eines periodischen Schwingungsverlaufs.
1
Periodendauer T 
Frequenz f
f
Die Frequenz f gibt die Anzahl der Schwingungen pro Sekunde an.
1
Frequenz f 
Periodendauer T
2