26 Wechselstromlehre

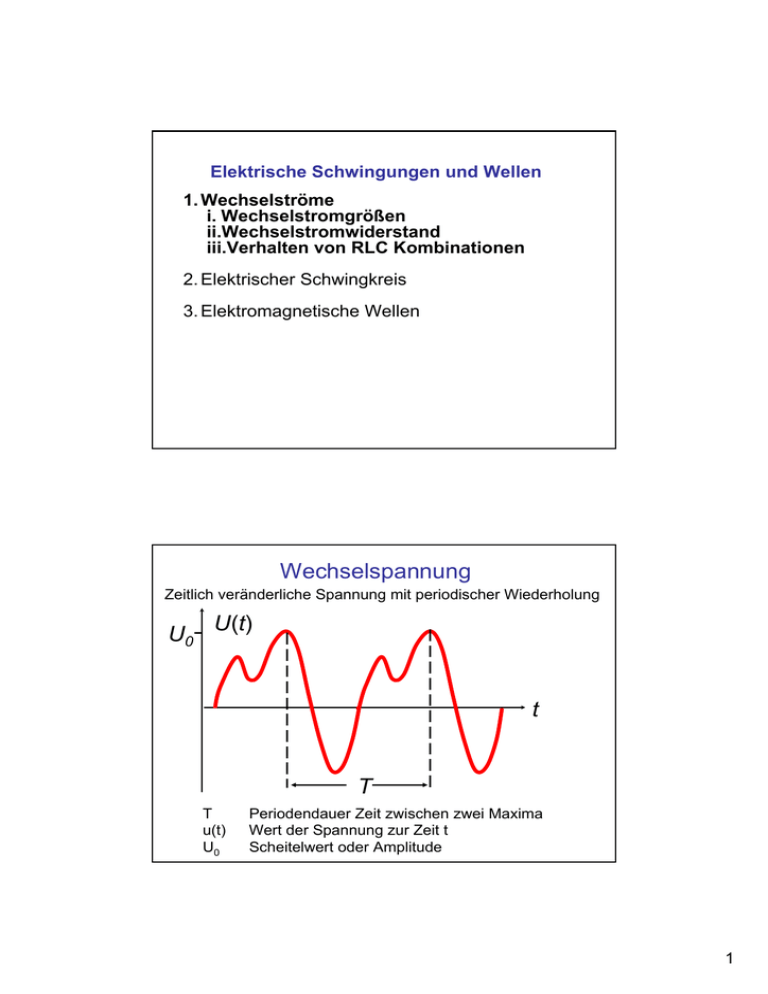
Elektrische Schwingungen und Wellen
1. Wechselströme
i. Wechselstromgrößen
ii.Wechselstromwiderstand
iii.Verhalten von RLC Kombinationen
2. Elektrischer Schwingkreis
3. Elektromagnetische Wellen
Wechselspannung
Zeitlich veränderliche Spannung mit periodischer Wiederholung
U0
U(t)
t
T
T
u(t)
U0
Periodendauer Zeit zwischen zwei Maxima
Wert der Spannung zur Zeit t
Scheitelwert oder Amplitude
1
Sinusförmige Schwingung
U(t)
+U0
-U0
U(t) = U0 sin (ω t + ϕ)
U0
ω
ν
T
ϕ
ωt + ϕ
Amplitude
Kreisfrequenz [ω] = 1/s
Frequenz [ν] = 1/s = 1Hz (Hertz)
Periodendauer [T] = s
Phasenverschiebung
„Phase“
ω = 2πν =
2π
T
Phase
U1(t)
U2(t)
t
∆ϕ
U1(t) = U01 sin (ω t + ϕ1)
U2(t) = U02 sin (ω t + ϕ2)
∆ϕ = ϕ1−ϕ2
Phasenverschiebung
2
Amplitudenverhältnisse
Verhältnis von zwei Amplituden V = A1/A2
Logarithmisches Maß v = log (V) = log (A1/A2)
Oft verwendete Definition in Elektrotechnik
logarithmiertes Verhältnis in Dezibel, dB
a:= 10 log (P1/P2)
a[dB] = 10 Logarithmus des Verhältnisses von zwei Leistungen
Leistung P proportional zu Spannung2 = U2
a = 10 log (P1/P2) = 10 log (U12/U22)
= 20 log (U1/U2)
a[dB] = 20 Logarithmus des Verhältnisses von zwei
Spannungen bzw. Strömen
Beispiel: U1 = U2
U1 > U2
U1 < U2
a = 0 dB
a > 0 dB
a < 0 dB
U1=100V U2=1V a = 40dB
U1=1V U2=10V a = -20dB
dB‘s
A = 20 log (Uout/Uin)
Verstärker A>0
Abschwächer A < 0
Uin
Uout
Wichtige Wert: -3dB entspricht halber Leistung
Uout: Uin = 1 :√2
+3dB entspricht doppelter Leistung Uout: Uin = √2 : 1
3
Wechselstromwiderstand
Gleichstromwiderstand R:= Spannung/Strom
Wie groß ist der Widerstand in Abhängigkeit der Frequenz für
Ohmschen Widerstand, Kondensator bzw Spule?
Strom- und Spannungsverlauf an
einem Ohmschen Widerstand
I(t)
U(t)
≈
Beobachtung:
Es fließt ein Strom
Strom ist unabhängig von Frequenz
R
4
Widerstand: Strom und Spannung
U(t) = U0 sin (ω t)
⇒ I(t) = 1/R U0 sin (ω t)
U(t)
I(t)
t
Wechselspannung erzeugt Wechselstrom durch Widerstand
Strom und Spannung sind in Phase
Der ideale ohmsche Widerstand ist frequenzunabhängig
Elektrische Leistung in einem Widerstand
Definition P = U x I
Ohmscher Verbraucher: Strom und Spannung in Phase
U(t) = U0 sin(ω t)
I(t) = I0 sin(ω t)
p(t) = U I = U0 sin(ω t) I0 sin(ω t) = U0 I0 sin2(ω t) = R I02 sin2(w t)
Momentanleistung
p(t)
U(t)
t
0
I(t)
Leistung oszilliert
Wie groß ist der Mittelwert P?
T
P=
T
1
1
p(t )dt = ∫ RI0 sin2 (ωt )dt =
∫
T0
T0
1 2
= RI0
2
5
Effektivwert
Wie kömmt man zu dem „Wurzel 2“ Faktor, oder wann gilt er?
Definition Effektivwert:
Ieff =
t
1 2
=
I (t ' )dt '
t ∫0
I (t )
2
„rms“ root mean square
T
Periodische Signale Integration über
eine Periode T
Ieff =
1 2
I (t ')dt '
T ∫0
Erzeugt eine Wechselstrom an einem ohmschen Verbraucher eine
bestimmte mittlere Leistung, so ist sein Effektivwert diejenige
Stromstärke, die ein Gleichstrom haben müsste, um am selben
Verbraucher die gleiche mittlere Leistung zu erbringen
Zusammenhang Ieff und
Spitzenwert f. ausgew. Kurven
Sinus WS Ieff = I0 / 2
Dreieck
Ieff = I0 / 3
Rechteck Ieff = I0
Effektivwert Netzspannung
Das elektrische Netz liefert Wechselspannung mit einer Frequenz von
50 Hz und einer Spannung von 230V
Was ist das eigentlich für eine Spannung?
Gemessen Spitzenwert ~ 320V
Nennwert 230 V
320/230 ~ 1.4 ~ √2
Bei Spannungen wird oft der Effektivwert angegeben
das ist jener Wert der die gleiche Leistung ergibt wie eine
Gleichspannung
Ueff = √2/2 U0 = 0.707 U0 für sinusförmige Spannung
Spannung und Strommessgeräte zeigen normalerweise den Effektivwert an!
Bei nichtsinusförmigen Signalen Vorsicht angebracht!
6
Strom und Spannungsverlauf
Kondensator
I(t)
U(t)
≈
Beobachtung:
Es fließt ein Strom
Strom wird mit zunehmender Frequenz mehr
Strom wird mit zunehmender Kapazität mehr
C
Zur Erinnerung
Strom ist Änderung der Ladung pro Zeit (I = ∆Q/∆t)
Ladung in einem Kondensator ist
Kapazität mal Spannung (Q = C U)
I = C dU/dt
Kondensator: Strom und Spannung
U(t) = U0 sin (ω t)
⇒ I(t) = ω C U0 cos (ω t) = ω C U0 sin (ω t + π/2)
U(t)
I(t)
t
Wechselspannung erzeugt Wechselstrom durch Kondensator
Der Strom eilt der Spannung um 90° voraus
Für Gleichspannung (ω = 0) ist der Strom 0
7
Wechselstromwiderstand Kondensator
U (t ) = U 0 cos(ωt ) = ℜ(U 0e iωt ) komplexe Schreibwei se
I (t ) = I0 sin(ωt + π / 2) = ℜ(I0e i (ωt +π / 2 ) ) = ℜωCU 0e i (ωt +π / 2 )
U 0e i (ωt )
1 i (−π / 2 )
1
U (t )
=
=
= −i
Xc =
e
i (ωt +π / 2 )
ωC
ωC
I (t ) ωCU 0e
−i
ωC
1
Xc =
ωC
Xc =
e iϕ = cos ϕ + i sin ϕ
e −iπ / 2 = −i
Komplexer Wechselstromwiderstand
Betrag des Wechselstromwiderstandes
Komplexer Widerstand beschreibt Frequenzabhängigkeit des Betrags
sowie die 90° Phasenverschiebung zwischen Strom und Spannung
Induktiver Widerstand
I(t)
≈
L
Beobachtung:
Es fließt ein Strom
Strom wird mit zunehmender Frequenz weniger
Strom wird mit zunehmender Induktivität weniger
Wechselspannung UE wird angelegt
dadurch fließt ein sich zeitlich änderner Strom
dadurch in der Spule eine Spannung induziert
Uind = L dI/dt
Nach Kirchoff UE= Uind
8
Strom und Spannungsverlauf an Induktivität
U(t) = U0 sin (ω t)
⇒ I(t) = 1/ (ω L) U0 (- cos (ω t)) = 1/ (ω L) U0 sin (ω t - π/2)
U(t)
I(t)
t
Wechselspannung erzeugt Wechselstrom durch Spule
Der Strom läuft der Spannung um 90° hinterher
Der induktive Wechselstromwiderstand XL = ω L
er nimmt mit zunehmender Frequenz und Induktivität zu
Für Gleichspannung (ω = 0) ist eine Spule ein Kurzschluss
Widerstandsbetrag und Phase
ϕ
Betrag
XC =
1
ωC
+
Phase
π
L
2
XL = ωL
ω
0
R
R
ω
−
π
2
C
9
Zusammenfassen von Widerständen
Wechselstromwiderstände haben einen Betrag und eine Phase
I(t)
R
I(t)
U(t)
Wie groß ist der
Gesamtwiderstand Zges?
C
UR(t)
Uc(t)
U(t)
U(t)= Zges I(t)
R und Xc können nicht einfach addiert werden, weil
Strom durch beide gleich aber
Spannung am Kondensator 90° nacheilend
Spannung am Widerstand in Phase
I(t)
UC(t)
UR(t)
t
Zusammenfassen von Widerständen
Widerstände werden als Zeiger (Vektoren in komplexer Ebene) aufgefasst
Betrag entspricht der Länge
Richtung der Phasenverschiebung zwischen Strom und Spannung
XL
UR
R
I
Strom in R und C gleich
UR = I R UR und I in Phase
UC = I |XC| UC 90° nacheilend zu I
ϕ
Uc
XC
Ohmscher Widerstand R x-Achse
kapazitiver Widerstand XC -90° verschoben
damit berücksichtigt U/I nicht in Phase
Zges
Z ges = R + X c = R −
Z = ℜ(Z ) + ℑ(Z )
2
ℑ(Z )
∠Z = tan ϕ =
ℜ(Z )
Z = Z e iϕ
i
ωC
Komplexer Widerstand
2
Betrag des Widerstands Impedanz
Phase des Widerstands
Polardarstellung
10
Zusammenfassen von Widerständen
Geg: R,L,C
I(t)
R
Ue = U0 sin(ωt) =Re U0 exp(iωt)
Ges: I(t)
Ue
1
Z = R + iωL − i
ωC
1 ⎞
⎛
2
⎜ ωL −
⎟
1 ⎞
ωC ⎠
⎛
2
⎝
tan
ϕ
Z = R + ⎜ ωL −
=
⎟
ωC ⎠
R
⎝
I (t ) =
I0 =
L
C
U e (t ) U 0e iωt U 0 i (ωt −ϕ )
e
=
=
Z
Z e iϕ
Z
U0
Betrag des Stromes
Z
ϕ Phasenvers chiebung des Stromes
gegenüber der Spannung
Leistung bei Wechselstrom
p(t)
U(t)
Ueff Ieff cos(ϕ)
I(t)
„Negative Leistung“
Energie von Verbraucher in
Quelle zurückgeliefert
P = U eff Ieff cos(ϕ )
S = U eff Ieff
B = U eff Ieff sin(ϕ )
cos(ϕ )
Wirkleistung:tatsächlich verbrauchte Leistung
Scheinleistung
Blindleistung: pendelt zwischen Quelle und
Verbraucher
Leistungsfaktor
11
Spannungsteiler
I(t)
R1
UE(t)
≈
R2
UA(t) = ?
Wie hängt die Ausgangsspannung von der Eingangsspannung ab?
Verhältnis V = UA/UE
Maschenregel 1: UE = I R1 + I R2
Maschenregel 2: UA = I R2
V =
UA
IR2
R2
=
=
U E IR1 + IR2 R1 + R2
Wenn R2 << R1 dann ist UA~ 0
Wenn R2 >> R1 dann ist UA~ UE
und V = 0
und V = 1
RC Tiefpass
Wenn ein Widerstand und ein Kondensator in Serie geschalten sind,
wie verhält sich die Eingangs UE zur Ausgangsspannung UA?
I(t)
R
UE(t)
≈
C
UA(t) = ?
IA(t) = 0
1
U A (t )
1
V (ω ) =
= iωC =
1
U E (t ) R +
1 + iRωC
iωC
1
V (ω ) =
tan ϕ = −RωC
2
1 + (RωC )
12
Frequenzgang eines Tiefpasses
V (ω )
1
∝
1
RC
1
ω RC
ω
Das Verhältnis von Ausgangs zu Eingangsspannung als Funktion der
Frequenz heißt Frequenzgang.
Werden die tiefen Frequenzen ohne Abschwächung (V = 1)
übertragen so spricht man von einem Tiefpass
Tiefe Frequenzen XC = 1/ωC >> R V ~ 1
Hohe Frequenzen XC = 1/ωC << R V~ 0
Tiefpass Frequenzgang
Näherung
0
Exakt
V (db)
-5
-10
τ = 1/RC
-15
Grenzfrequenz
ωg= 1/τ
-20
-25
0.01
0.1
10
1
0.11
Frequenz
Normierte
Frequenz ω/ωg
ω < ωg: V(dB) = 0
ω = ωg: V(dB) = -3dB
ω > ωg: V(dB) <0
Abfall -20db pro
Dekade
100
10
13
Tiefpass als Integrator
UE
Rechteckspannung an
RC Tiefpass angelegt
Fourierzerlegung
Berechnung der Amplituden und Phasen am Ausgang
Addition der Schwingungen (Fouriersynthese)
UA
Näherung
1
1 U
1
U A = UC = ∫ Idt ≈ ∫ E dt =
U E dt
C
C R
RC ∫
Ausgangsspannung (ungefähr) gleich zeitliches Integral der
Eingangsspannung: Tiefpass ist Integrator
RC Hochpass
C
UE(t)
≈
R
UA(t) = ?
IA(t) = 0
U A (t )
R
iωCR
=
=
1 + iRωC
U E (t ) R + 1
iωC
1
ωCR
tan ϕ =
V (ω ) =
2
RωC
1 + (RωC )
V (ω ) =
14
Frequenzgang eines Hochpasses
V (ω )
1
ω RC
1
RC
ω
Werden die hohen Frequenzen ohne Abschwächung (V = 1)
übertragen so spricht man von einem
Hochpass
Hochpass Frequenzgang
Näherung
0
Exakt
-10
τ = 1/RC
ω > ωg: V(dB) = 0
ω = ωg: V(dB) = -3dB
ω < ωg: V(dB) <0
Grenzfrequenz
ωg= 1/τ
Abfall -20db pro
Dekade
-20
-30
-40
-50
-60
0.01
0.1
1
10
Normierte Frequenz ω/ωg
15
Hochpass als Differenzierglied
UE
Rechteckspannung an
RC Hochpass angelegt
Fourierzerlegung
Berechnung der Amplituden und Phasen am Ausgang
Addition der Schwingungen (Fouriersynthese)
UA
Näherung
U A = U R = RI ≈ R
dQ
dU E
= RC
dt
dt
Ausgangsspannung (ungefähr) gleich zeitliches Differenzial der
Eingangsspannung: Hochpass ist Differnziator
RL Hoch und Tiefpass
UE(t)
≈
L
UE(t)
R
UA(t)
≈
R
L
UA(t)
LR Tiefpass
LR Hochpass
ω = 0 XL = 0
ω = 0 XL = 0
keine Spannung an L: UA = UE
kein Spannung an L: UA ~ 0
ω >> XL sehr groß
ω >> XL sehr groß
ganze Spannung an L: UA ~ 0
ganze Spannung an L: UA = UE
16
Schaltvorgänge
Achtung:
Bei der Beschreibung transienter Vorgänge (EinAusschalten usw.) ist die Verwendung des
Wechselstromwiderstandes Z unzulässig
Z gilt nur für Anregung mit sinusförmiger
Wechselspannung!!!
Schalten: Gleichspannung wird eingeschaltet,
einmaliger Sprung, Verlauf
Allerdings Maschenregel darf angewendet werden (aber
richtig)
17