n - mpg-trier.de

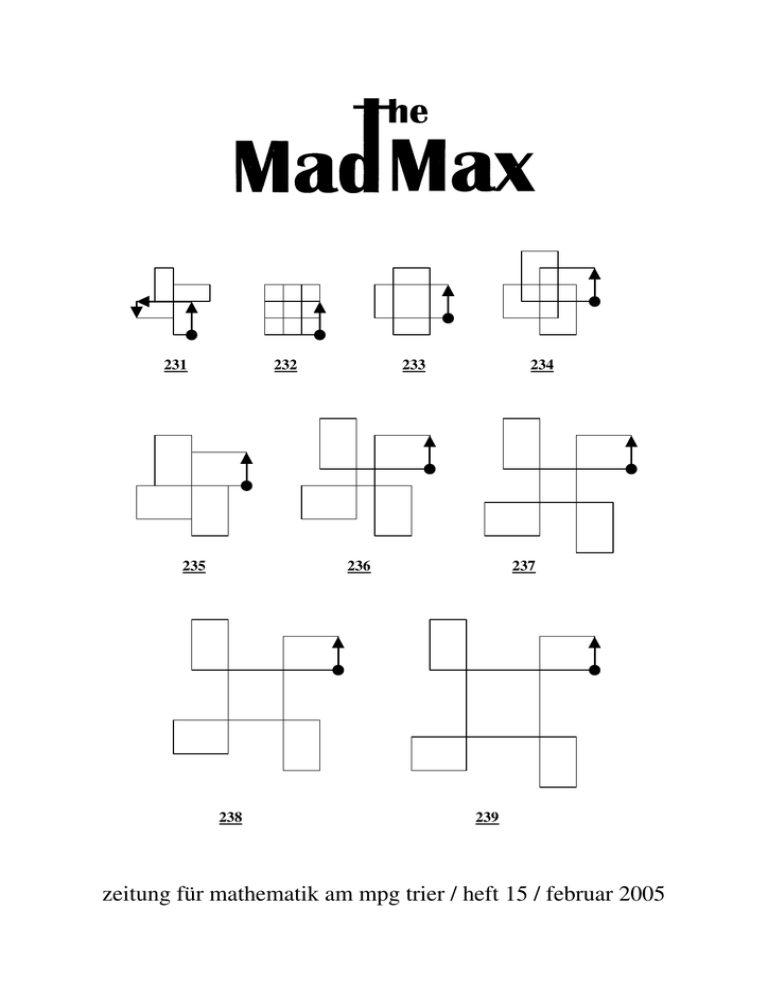
231
232
235
233
234
236
238
237
239
zeitung für mathematik am mpg trier / heft 15 / februar 2005
Ein dummer Roboter
Wir haben in der Mathe-AG einen dummen Roboter
kennen gelernt. Er kann nur gerade aus laufen und um
90° nach links abbiegen. Zuerst
konnte er sich nur eine Zahl
merken. Deshalb lief er nur im
Quadrat rum:
Im ersten Beispiel läuft er immer 3 cm gerade aus, ehe
er sich um 90° dreht, im zweiten Beispiel läuft er 2 cm,
ehe er die Richtung ändert.
Später brachten wir ihm bei, sich zwei Zahlen zu
merken. Aber das war auch nicht gut, denn nun lief er
ein Rechteck (außer bei zwei gleichen Zahlen; dann läuft
er wieder ein Quadrat und das kennen wir ja schon):
(3;5)
(2;1)
(1;2)
Das war also immer noch langweilig. Deshalb brachten
wir ihm bei sich, noch eine weitere Zahl zu behalten.
2
Jetzt wurde es interessant (Startpunkt und erste
Wegstrecke sind immer markiert):
231
232
235
233
234
236
237
238
239
Der Roboter kommt immer wieder zu seinem Startpunkt
zurück. Dabei durchläuft er eine Figur, die aussieht wie
die Flügel einer Windmühle. Dabei haben wir folgendes
festgestellt:
3
Ergebnis:
Die ersten beiden Ziffern sagen immer aus wie groß
und breit die äußeren Kästchen sind. Dabei entscheidet
die dritte Ziffer wie weit voneinander diese äußeren
Kästchen sind; sie entscheidet auch wie groß das
mittlere Kästchen ist: man muss nur die beiden andern
Zahlen subtrahieren..
Wir haben dann noch genauer untersucht, was passiert,
wenn man bei drei Zahlen zwei Gleiche hat. In den
folgenden Beispielen haben wir den Roboter mit den
Zahlen 1 1 n laufen lassen wobei n zuerst auch 1 war,
dann 2,3,4 und zuletzt 5:
Wir erhalten hier genau die Figuren wie vorher, nur
entstehen wegen der zwei gleichen Zahlen Quadrate,
deren Seitenlänge so groß ist wie die beiden gleichen
Zahlen; hier also 1. Die Seitenlänge s des mittleren
Quadrates können wir auch berechnen: s = n – 2 mal 1.
Außerdem ist es völlig egal wo die andere Zahl
eingeordnet ist.
411
141
4
114
Spaziergänge auf dem Schachbrett
Wir haben uns mit einem ganz normalen Schachbrett
beschäftigt und dabei sind wir auf eine ganz interessante
Frage gestoßen.
1. Material und Anfangsstellung
Der Spielplan besteht aus 64 gleichgroßen Feldern, und
zwar 8 senkrechten und 8 waagerechten Reihen. Wir
platzieren nun eine Spielfigur in die linke obere Ecke des
Schachbrettes.
S
S = Start der Spielfigur
Z = Ziel
Z
2. Regel für die Fortbewegung der Figur
Die Spielfigur, die in der linken, oberen Ecke des
Schachbrettes steht, soll in die rechte untere Ecke
dieses Schachbrettes gelangen. Die Figur darf aber aus
der Draufsichtperspektive nur nach rechts und nach
unten bewegt werden.
3. Die Frage
Wie viele verschiedene Wege gibt es, um in die rechte
untere Ecke zu gelangen?
5
Dabei interessierte uns auch, wie sich die Möglichkeiten
verändern, wenn bestimmte Felder des Schachbrettes
gesperrt wären.
4. Die Lösung
4.1 Ohne Sperrung eines Feldes
Um eine Lösung und Regelmäßigkeit zu erkennen,
betrachteten wir zunächst Schachbretter ohne
Sperrung eines Feldes und zwar geordnet nach
verschiedenen Größen.
Zuerst beschäftigten
Kästchenfeld.
wir
uns
mit
einem
2x2
Es gibt nur eine Möglichkeit in die äußeren
Felder zu gelangen. Für das rechte untere
1
Feld Z gibt es demnach 2 Möglichkeiten, denn
aus den beiden äußeren Feldern kann man
sich nur auf eine Art weiterbewegen. Man hat also
1+1=2 Möglichkeiten. Die vollständige Lösung für ein
2x2 Feld sieht also wie unten angegeben aus.
S
1
S
1
1
2
Hieraus leiteten wir die folgende Regel ab:
Wenn ein Feld leer ist, ergibt sich die Lösung für die
Wege dieses Feldes aus der Summe des links
danebenliegenden und des oberhalb liegenden
Feldes.
6
Bei einem 3x3 Feld untersuchten wir, ob diese Regel
sich ebenfalls als richtig
erwies. Wir erhielten
folgende Lösungen:
S
1
1
2
1
In der ersten Spalte bleibt senkrecht und
waagerecht immer nur eine Möglichkeit.
1
S
1
1
1
2
3
1
3
S
1
1
1
2
3
1
3
6
Auch hier ergibt sich die Lösung für die
Felder nach der Regel als Summe des
links
danebenliegenden
und
des
oberhalb liegenden Feldes.
Die Regel bestätigt sich auch bei dem
rechten unteren Feld Z. Es ergeben sich
also 3+3=6 mögliche Wege, um von dem
Feld S in das Feld Z zu gelangen.
So überprüften wir für viele Größen von Schachbrettern die möglichen Lösungswege. Es folgen noch
drei Beispiele:
4x4 Feld
S 1
1 2
1
3
1
4
1 3 6 10
1 4 10 20
7
6x6 Feld
8x8 Feld
S
1
1
1
1
1
1
2
3
4
5
6
1
3
6
10 15
21
1
4
10 20 35
56
1
5
15 35 70
126
1
6
21 56 126 252
S
1
1
1
1
1
1
1
1
2
3
4
5
6
7
8
1
3
6
10
15
21
28
36
1
4
10
20
35
56
84
120
1
5
15
35
70
126 210
330
1
6
21
56
126 252 462
792
1
7
28
84
210 462 924
1716
1
8
36
120 330 792 1716 3432
Es gibt also 3432 verschiedene Wege um bei einem 8x8
Feld von der linken oberen Ecke in die rechte untere
Ecke zu gelangen.
Betrachtet man diese Lösung, so ergibt sich eine
Symmetrieachse, nämlich die Diagonale.
8
4.2 Mit Sperrung eines Feldes
Anschließend untersuchten wir, wie sich die Anzahl der
möglichen Wege veränderte, wenn einzelne Felder
gesperrt werden. Die gesperrten Felder dürfen nicht
betreten werden, wodurch sich natürlich die Zahl der
Wege von S nach Z verkleinert.
Beispiel 1: Untersuchung des 2x2 Feldes mit S G
G als gesperrtem Feld. Es gibt nur eine
1
Möglichkeit das Feld Z zu erreichen. Auch hier 1
gilt: Das Ergebnis errechnet sich wieder als
Summe des links danebenliegenden und des darüberliegenden Feldes, wobei das Feld G den Wert 0 hat.
Rechnung: 1+0= 1.
Beispiel 2: Sperrt man das S 1
1
1
1
angegebene Feld G, so erhält
G 1
2
3
man 54 Wege um das Feld Z zu 1
erreichen. Die Anzahl der 1
3
6
6
7
möglichen Wege nach Z zu
gelangen verringert sich also 1
4
10 16 23
erheblich bei Sperrung dieses
5
15 31 54
Feldes. Ohne Sperrung hätten 1
sich nämlich 70 Wege ergeben,
wie man an dem 5x5 Feld weiter oben erkennen kann.
S
35
55
65
69
35 55 65 69 Für die systematische Untersuchung des 5 x 5 Brettes tragen
30 40 54 65 wir die Zahl 54 in das Feld G ein.
40 34 40 55 Entsprechend haben wir für alle
Sperrfelder die Anzahl der Wege
54 40 30 35 von S nach Z bestimmtund in der
Tabelle eingetragen. Es gibt
65 55 35 Z immer
vier
symmetrisch
9
zueinander liegende Felder mit der gleichen Anzahl von
Wegen.
Diese Symmetrie haben wir bei allen Feldgrößen
festgestellt, wie die nächsten Beispiele zeigen.
5x5 Feld
S
35 55 65 69
35 30 40 54 65
55 40 34 40 55
65 54 40 30 35
69 65 55 35 Z
8x8 Feld
S
1716 2640 3102 3312 3396 3424 3431
1716 1584 2046 2592 3012 3264 3383 3424
2640 2046 1920 2172 2592 2991 3264 3396
3102 2592 2172 2032 2207 2592 3012 3312
3312 3102 2592 2207 2032 2172 2592 3102
3396 3264 2991 2592 2172 1920 2046 2640
3424 3383 3264 3012 2592 2046 1584 1716
3431 3424 3396 3312 3102 2640 1716 Z
10
Wenn man größere Quadratzahlen ausrechnen will,
muss man immer wieder multiplizieren. Ich habe mich
gefragt, ob das auch einfacher geht. Eines Tages fand
ich dann durch Zufall eine Formel, weil mir in einigen
Beispielen auffiel, dass man die nächste Quadratzahl
einfach aus der vorangehenden erhalten kann:
Beispiele:
16 + 4 + 5 = 25
5 2 = 25
25 + 5 + 6 = 36
6 2 = 36
36 + 6 + 7 = 49
5 2 = 25
6 2 = 36
7 2 = 49
4 2 = 16
Wie man sieht, muss man zur alten Quadratzahl nur die
Zahl und ihren Nachfolger addieren.
2
2
Behauptung: (n + 1) = n + n + (n + 1)
Für n = 5 kann man sich die Gültigkeit dieser Formel in
einer Zeichnung klar machen:
11
Wenn man zu den 4² = 16 kleinen Kreisen die vier
Quadrate und die fünf Kreise mit Kreuzen dazunimmt
hat man 5² = 25 Symbole.
Allgemein kann man die Formel beweisen, wenn man
die 1. Binomische Formel verwendet:
(n + 1) 2 = n 2 + 2 ⋅ n ⋅ 1 + 12
= n 2 + 2n + 1
= n2 + n + n +1
= n 2 + n + ( n + 1)
Viel Spaß beim Ausprobieren.
Noch´n Witz
Ein Mathematiker, ein Physiker und ein Biologe sitzen im
Zug und fahren durch Schottland. Während der Fahrt
sehen sie auf einer Wiese ein schwarzes Schaf, worauf
der Biologe meint: "Ah, ich sehe, dass die schottischen
Schafe schwarz sind."
Der Physiker sagt: " Du meinst wohl, dass manche
schottischen Schafe schwarz sind."
Darauf der Mathematiker: "Nein, wir wissen lediglich,
dass es in Schottland mindestens ein Schaf gibt, und
dass wenigstens eine Seite dieses Schafes schwarz ist."
12
Wenn Leute von einem Viereck sprechen, meinen sie
häufig ein Quadrat oder ein Rechteck:
Vierecke müssen aber keine rechten Winkel haben:
Drache
Trapez
Parallelogramm
Sie können auch völlig unsymmetrisch sein:
Das gilt auch für Figuren mit 3,5,6,... Ecken, sogenannte
n-Ecke.
7-Eck
13
Wie viele rechte Winkel kann ein n-Eck nun maximal
haben (Als rechte Winkel zählen Innen- und Außenwinkel mit 90°)?
Ausprobieren:
6-Eck= 6 rechte Winkel?
8-Eck= 6 rechte Winkel?
Am besten erkennt man die Zahl der rechten Winkel bei
der Treppenmethode, weil dies ein festes Schema ist:
8-Eck= 8 rechte Winkel!
9-Eck= 7 rechte Winkel!
In der folgenden Tabelle sind alle Ergebnisse zusammen
gefasst:
14
n 3
rw 1
4
4
5
3
6
6
7
5
8
8
9
7
...
...
Feststellung:
Bei gerader Eckanzahl (n) ist die maximale Zahl der
rechten Winkel gleich der Anzahl der Ecken.
Bei ungerader Eckanzahl (n) ist die maximale Zahl der
rechten Winkel um 2 geringer als die Anzahl der Ecken.
Abgekürzt:
n= gerade
⇒
rW= n
n= ungerade
⇒
rW= n-2
(rW= maximale Anzahl der rechten Winkel)
Beweis:
1. n gerade: ,,Treppe“
2
3
4
ungerade
5
1
,,Treppe“ schließt in der geraden
n-ten Ecke
15
Hier sieht man, dass es bei gerader Eckanzahl auf jeden
Fall genauso viele rW wie Ecken geben kann. Mehr rW
als Ecken sind natürlich nicht möglich.
2. n ungerade:
Graphische Begründung dafür, dass es mit der Treppenmethode im Idealfall n-2 rechte Winkel gibt:
2
3
4 5
6
7
gerade
,,Treppe“ schließt in der
ungeraden n-ten Ecke
Ecken sind nicht rechtwinklig
Nach der Treppenmethode erstellte n-Ecke können also
bei ungeradem n höchstens n – 2 rechte Winkel haben.
Es könnte aber noch irgendwie anders gebaute n-Ecke
geben, die n – 1 oder sogar n rechte Winkel haben.
Gegenbeweis:
Um den Gegenbeweis zu verstehen, muss erst etwas
erklärt werden:
16
1. Die Winkelsumme im Dreieck beträgt 180°.
Im Viereck ist sie 2mal so groß: 360°.
Da Mathematik logisch aufgebaut ist, setzt sich die
Reihe so fort:
5-Eck= 3mal 180°= 540°
6-Eck= 4mal 180°= 720°...
Winkelsumme beim 7-Eck= 5*180°
2. Wenn der Außenwinkel 90° ist, dann ist der
Innenwinkel 270° und kann in 90° + 180° zerlegt
werden:
90°
180°
Im folgenden soll y die Anzahl
der Außenwinkel mit 90° sein.
Jetzt geht es los:
1.Annahme:
Es gibt n rechte Winkel.
Dann kann man die Winkelsumme auf zwei Arten
angeben. Nach der Formel für die Winkelsumme im nEck ist die Summe gleich (n − 2) *180° .
⇒ ( n − 2) *180° = n * 90° + y *180°
⇔ n *180° − 360° = n * 90° + y *180° | + 360° − n * 90°
⇔ n * 90° = 180° * y + 360° |: 90°
⇔ n = 2* y + 4
⇔ n = 2 * ( y + 2)
17
Nach der letzten Zeile müsste n dann eine gerade Zahl
sein, obwohl wir uns gerade mit ungeradem n
beschäftigen. Also ist unsere erste Annahme falsch.
2.Annahme:
Es gibt n-1 rechte Winkel
α=
der nicht rechte Winkel
(n − 2) *180° = (n − 1) * 90° + y *180° + α
⇒ (n − 2) *180° − (n − 1) * 90° − y *180° = α
⇔ n *180° − 360° − n * 90° + 90° − y *180° = α
⇔ n * 90° − 360° + 90° − y *180° = α
⇔ (n + 1) * 90° − 360° − y *180° = α
α=
Vielfaches von
180°, was aber nicht
sein kann!
Vielfaches von 180°,
weil n+1 gerade ist
Ergebnis:
Es kann bei ungeradem n max. n-1 rW geben!
Noch´n Witz
Warum werden bei BMW neuerdings keine Mathematiker mehr beschäftigt?
Die haben allgemein ein Auto mit n Rädern konstruiert
und erst danach den Spezialfall n=4 betrachtet ...
18
Wie oft kann man ein Blatt Papier knicken?
1. Worum geht es?
Was denkt ihr, wie oft man ein Blatt Papier, das bis zum
Mond reicht in der Mitte knicken kann?
Das Gleiche haben wir uns auch gefragt. Zuerst haben
wir uns darauf geeinigt, dass wir stets nur in eine
Richtung knicken, also nicht einmal nach oben und
danach nach rechts.
Danach haben wir es in der Praxis mit einem DIN A 4
Blatt ausprobiert. Dabei haben wir es sechs Mal
geschafft. Jetzt haben wir uns überlegt, ob man es mit
großem Kraftaufwand schafft, das Blatt sieben mal zu
knicken. Bei uns hat es nicht geklappt. Wir suchten nach
dem Grund und kamen darauf, dass es vielleicht nicht
an der angewendeten, oder besser nicht angewendeten,
Kraft liegt, sondern an einem anderen Problem. Und
genau so ist es. Im folgenden beweisen wir, dass man
das Blatt rein mathematisch nur sechs Mal knicken
kann.
2. Vereinbarungen:
Wenn man vernünftige Berechnungen führen will, muss
man ein paar Vereinbarungen treffen:
- das Blatt wird immer in der Mitte und nur in eine
Richtung geknickt
- bei unseren Zeichnungen zeichnen wir den
geknickten Teil der Übersicht halber mit Rechtecken
anstatt Halbkreisen
19
- Bei dem Knick eines Blattes wird das Blatt innen
gestaut und außen gedehnt. Der Querschnitt des
Blattes ist die Anfangslänge und bleibt immer gleich
lang.
- Der bereits geknickte Teil eines Blattes wird
Verlustmenge genannt. Die Verlustmenge kann
nicht erneut geknickt werden.
- Der noch ungeknickte Teil wird x genannt. Wenn
x ≤ 0, dann lässt sich das Blatt nicht mehr knicken
(eher würde es reißen).
3. Erste Gedanken:
Als Erstes haben wir aufgezeichnet, wie das Blatt
ungeknickt und geknickt aussieht:
0.
1.
2.
20
3.
4. Verlustmengenberechnungstabelle:
Im zweiten Schritt haben wir uns überlegt, dass bei
jedem Knick eine bestimmte Menge Papier verloren
geht. Wir haben uns überlegt, wie man diese
Verlustmenge berechnen kann. Dazu haben wir
folgende Tabelle entwickelt.
A
1 Knick
2 1.
3 2.
4 3.
5 4.
6 5.
7 6.
8 7.
9 8.
10 9.
11 10.
B
C
Links Rechts
0
2
2
8
10
32
42
128
170
512
682
2048
2730 8192
10922 32768
43690 131072
174762 524288
D
Gesamtverlustmenge
2
10
42
170
682
2730
10922
43690
174762
699050
Um das Blatt 10 Mal zu knicken benötigt man also ein
Blatt mit einer Länge von mindestens 699050, wobei die
Maßeinheit die gleiche sein muss, wie die Einheit der
Dicke d , wobei diese in unserem Beispiel 1 ist. Jetzt ist
die ungeknickte Menge x Null.
21
5. Tabellenerklärung:
Die Tabelle erklärt sich folgendermaßen:
A
1 Knick
2 1.
3 2.
4 3.
5 4.
6 5.
7 6.
8 7.
9 8.
10 9.
11 10.
B
C
Links
Rechts
0
d*2
(C2)+(B2) (C2)*4
(C3)+(B3) (C3)*4
(C4)+(B4) (C4)*4
(C5)+(B5) (C5)*4
(C6)+(B6) (C6)*4
(C7)+(B7) (C7)*4
(C8)+(B8) (C8)*4
(C9)+(B9) (C9)*4
(C10)+(B10) (C10)*4
D
Gesamtverlustmenge
(C2)+(B2)
(C3)+(B3)
(C4)+(B4)
(C5)+(B5)
(C6)+(B6)
(C7)+(B7)
(C8)+(B8)
(C9)+(B9)
(C10)+(B10)
(C11)+(B11)
Man siehe in der Zeichnung nach dem ersten Knick: Auf
der linken Seite ist das Blatt noch ungeknickt, während
auf der rechten Seite die geknickte Menge (also die
Verlustmenge) genau doppelt so groß ist, wie das Blatt
dick ist. Also: d*2.
Nach dem zweiten Knick kommt die Verlustmenge, die
vorher rechts war auf die linke Seite und die
Verlustmenge, die schon vorher links war bleibt dort.
Rechts wird die vorherige Verlustmenge vervierfacht.
So geht es weiter: Die rechte Verlustmenge (die schon
vervierfacht wurde) kommt auf die linke Seite und rechts
wird erneut vervierfacht, also schon insgesamt
versechzehnfacht.
Alles, was links ist bleibt dort und erhält immer das dazu,
was vorher rechts war.
22
Jetzt haben wir uns weiter überlegt:
Knick
Links
Rechts
1
2
3
4
0
d*2
d*2 + d*2*4
d*2 + d*2*4
d*2*4*4
d*2
d*2*4
d*2*4*4
+ d*2*4*4*4
u.s.w.
Wenn man nun z.B. beim dritten Knick 2d ausklammert
ergibt sich folgendes:
Links
Rechts
Links + Rechts
2d*(40+41)
2d*(42)
2d*(40+41+42)
Also:
x = 2d*(40 + 41 + 42) | : 2
x = d*(21 + 23 + 25)
Wenn man dieses Verfahren beim
anwendet, ergibt sich:
x = 2d*(40 + 41 + 42 +.......+ 4n-1) | : 2
x = d*(21 + 23 + 25 +.......+22n-1)
n-ten
Knick
Wenn man jetzt herausfinden will wie lang ein Blatt mit
der Dicke eins sein muss, um es neun Mal knicken zu
können, dann setzt man für n 9 ein und rechnet aus: 22*91
= 217
Jetzt vervollständigt man die Reihe:
21 + 23 + 25 +...+ 215 + 217
= 2+8+32+...+32768+131072
23
Wenn man das nun ausrechnet kommt 174762 heraus.
Also muss das Blatt 174762 lang sein (in der gleichen
Einheit wie die Dicke).
Wenn die Dicke nicht 1, sondern die übliche Papierdicke
von 0,06mm beträgt, multipliziert man das Ergebnis nicht
mit 1, sondern mit 0.06, also:
174762*0,06mm=10485,72mm=1,048572m ~ 1,05m
Das Blatt muss also ungefähr 1,05 Meter lang sein.
Dieses Verfahren ist sehr aufwändig, da man für die
Lösung immer die Summe einer ganzen Zahlenreihe
ausrechnen muss. Deshalb haben wir versucht eine
einfachere Formel zu finden.
Unser Beispiel zeigt, dass man nach dem neunten Knick
bei einer Dicke von 1 eine Länge von 21 +23 +25+ ... +
217 = 174762 braucht.
Wir haben herausgefunden, dass man die Summe von
20 + 21 + 22 + ... + 217 in „Blöcke“ aufteilen kann, nämlich
20 + 21 ;
22 + 23 ; 24 + 25 ; usw.
Da 21 das Doppelte von 20 ist gilt: 21 = 2/3 * (20 + 21)
Da 23 das Doppelte von 22 ist gilt: 23 = 2/3 * (22 + 23)
u.s.w.
2/3* (20 + 21) + 2/3 * (22 + 23) + ... + 2/3 * (216 + 217) =
174762
2/3* (20+21+22+…+216+217) = 174762
Jetzt muss man das Binärsystem ins Spiel bringen:
Mit einer Ziffer im Binärsystem kann man maximal 21 – 1
= 20 darstellen, denn 12 = 1.
24
Mit zwei Ziffern im Binärsystem kann man maximal 22 –
1 = 20+21 darstellen, denn 112 = 3.
Mit drei Ziffern im Binärsystem kann man maximal 23 – 1
= 20+21+22 darstellen, denn 1112 = 7,
u.s.w.
Übertragen in unser Problem heißt das:
218 – 1 = 20 + 21 + … + 216 + 217
Also gilt:
2/3* (20+21+22+…+216+217) = 2/3* (218 - 1)
Wenn man dies nun verallgemeinert ergibt sich:
Verlustmenge = 2/3 * (22n – 1)
6. Bedeutung der Verlustmenge:
Man kann ein Blatt nur so oft knicken, solang die
Verlustmenge kleiner als die Länge des Papiers ist.
Während man ein DIN A 4 Blatt nach unserer Formel
(und in Wirklichkeit) noch locker 6 Mal knicken kann,
braucht man für 9 Knicke schon etwa 1 m (siehe oben).
Dann geht die Länge schnell in die Höhe: Ein Blatt
Papier mit einer Länge von 1 km (=1000000 mm) kann
man nur zwölf Mal knicken und ein Blatt Papier, das so
lang ist wie die Entfernung Erde – Mond (ca. 384 000
km) kann man nur 21 Mal knicken.
25
Die Zahlentreppe
Wir haben uns damit beschäftigt, wie man aus vier
nebeneinander stehenden Zahlen eine neue Zahlenreihe
bekommt:
Vier beliebige Zahlen bilden unsere Startreihe. Nun gehen wir
eine Stufe runter. Dazu muss man die 1. und 2. Zahl
voneinander subtrahieren und die Differenz unter die erste
Zahl schreiben. Jetzt muss man das Gleiche mit der zweiten
und dritten Zahl, mit der dritten und vierten und mit der
vierten und ersten Zahl machen.
Zum Beispiel:
43
26
17
2
15
7
8
35
Start
1.Stufe
Das kann man nun solange wiederholen, wie man
möchte.
In unserem Beispiel sieht das so aus:
43
26
24
19
4
17
2
5
23
4
15
7
28
19
4
8
35
9
15
4
Start
1.Stufe
2.Stufe
3.Stufe
4.Stufe
Überraschung
Die letzte Reihe besteht vier gleichen Zahlen! Ist das immer
so?
26
Wir haben das Ganze mit anderen Startzahlen wiederholt:
22
56
21
14
78
35
7
14
43
28
21
14
15
7
7
14
12
16
7
15
12
28
9
22
3
12
37
31
25
15
12
6
6
10
3
12
Oder:
In der Tat landet man immer bei vier gleichen Zahlen. Ist das
Zufall oder passiert das wirklich immer? Wenn man noch eine
Stufe tiefer geht, dann besteht die letzte Reihe sogar nur aus
Nullen.
Wir schauen genauer hin:
Wenn man sich die Beispiele anschaut sieht man, dass die
größte Zahl einer Reihe immer kleiner wird. Das ist so, weil
durch die Differenzen die Zahlen der nächsten Reihe immer
kleiner werden. Wir haben aber auch Beispiele gefunden, wo
die größte Zahl nicht immer kleiner wird. Was passiert zum
Beispiel im folgenden Fall, wenn Nullen am Start stehen?
45
0
86
23
45
86
63
22
Hier steht wie in der ersten Reihe auch in der zweiten Reihe
die 86 als größte Zahl. Aber es dauert einfach eine Stufe mehr,
27
bis die größte Zahl kleiner wird. In der nächsten Reihe ist
die größte Zahl jetzt 41 und die ist kleiner als 86:
45
45
41
0
86
23
86
63
41
23
22
23
Bei zwei Nullen dauert es noch eine Stufe länger. Bei
drei Nullen landet man nach vier Stufen bei vier Nullen,
wenn vier Nullen da sind verändern sich die Zahlen nicht
mehr weil nur noch Nullen am Start sind.
0
0
32
0
32
12
32
20
8
12
12
12
0
0
0
23
0
0
23
23
0
23
0
23
23
23
23
23
Ähnlich ist es, wenn zwei gleiche Zahlen in einer Reihe
stehen:
22
22
31
12
0
9
19
10
9
10
9
10
Man erhält eine Null und damit geht es genauso weiter
wie in dem letzten Beispiel:
28
22
13
22
47
9
9
25
25
0
16
0
16
16
16
16
16
In diesem Beispiel stehen die zwei gleichen Zahlen nicht
nebeneinander, was aber auch nichts macht.
Verallgemeinerung
Wir haben uns nun überlegt, was passiert, wenn man mit
2, 3, 5, 6, ...Startzahlen beginnt.
Wenn man es mit 2 Zahlen macht, dann kommen direkt
zwei gleiche Zahlen heraus. Wie man an dem Beispiel
(hier unterhalb) erkennen kann.
562
473
89
473
Bei drei Zahlen wird es spannender, wie das folgende
Beispiel zeigt:
56
32
19
13
6
5
1
4
24
13
6
7
1
6
5
1
29
37
19
13
6
7
1
4
3
Die Zahlen werden immer kleiner und es sieht so aus,
als ob man wieder bei lauter Nullen landet. Wir machen
weiter:
3
1
0
1
1
0
2
1
1
0
1
1
1
2
1
1
0
1
Wir landen bei zwei gleichen Zahlen und einer Null. Die
dritte und die sechste Zeile zeigen, dass man keine
Chance hat, bei drei gleichen Zahlen zu enden. Das ist
bei drei Startzahlen immer so, außer wenn man mit drei
gleichen Zahlen anfängt. Aber das ist uninteressant und
macht keinen Spaß.
Mit fünf Zahlen sieht es ähnlich aus:
24
11
9
20
3
2
1
19
16
14
13
6
6
35
20
29
17
5
1
20
3
2
1
7
0
4
15
49
12
22
4
21
17
5
3
8
7
4
3
30
64
37
34
26
25
4
12
2
11
1
3
7
4
27
3
8
1
19
16
14
13
12
4
10
3
3
2
1
1
1
0
1
0
1
1
0
0
0
1
0
0
0
0
1
1
1
0
0
1
1
1
1
0
1
0
0
1
1
0
0
0
1
0
0
1
0
1
0
0
0
1
1
1
0
1
0
1
0
0
1
1
0
0
1
1
1
0
0
1
0
0
0
1
1
1
1
0
1
0
1
0
1
2
0
1
0
1
1
0
0
1
0
0
0
0
1
1
1
1
1
0
Bei fünf Zahlen wiederholen sich nach vielen Stufen
wieder die Zahlen. In diesem Beispiel waren das 14
Stufen. Am Ende waren immer drei Nullen und zwei
Einsen da.
Auch bei sechs Zahlen landet man nicht bei einer Reihe
gleicher Zahlen. Oder vielleicht doch? Versucht es doch
selber mal!
Noch´n Witz: "Die Ehe des Professors soll sehr
unglücklich sein, habe ich gehört!"
"Wundert mich nicht. Er ist Mathematiker, und sie
unberechenbar."
31