Nullstellen von quadratischen Funktionen

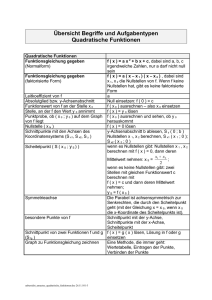
Mathematik – Gleichungen und Funktionen – Funktionen – Quadratische Funktion – Sellmer
Nullstellen von quadratischen Funktionen
Quadratische Funktionen weisen besondere Eigenschaften auf: Sie sind symmetrisch zur
Scheitelpunktsachse, haben einen Hoch- oder Tiefpunkt und sind links- oder rechtsgekrümmt. Eine weitere
Eigenschaft sind die Nullstellen (wo die Funktion die x-Achse schneidet). Quadratische Funktionen haben
entweder keine, eine oder sogar zwei Nullstellen. Die Berechnung von Nullstellen ist nicht nur eine große
Hilfe zum Zeichnen der Funktionen, sie ist auch von entscheidender Bedeutung beim Bestimmen von
Sachverhalten (Wie weit fliegt ein Speer bei einer bestimmten Geschwindigkeit und einem bestimmten
Wurfwinkel? Nach wie viel Sekunden muss ein Fallschirmspringer seine Reißleine ziehen?).
Bei Funktionen in der Form „ax2“ und „ax2 + c“ ist die Nullstellenberechnung ziemlich einfach, denn hier
muss man nur das „a“ und das „c“ auf die andere Seite bringen und anschließend die Wurzel ziehen.
Beispiele: Die Nullstellen folgender Funktionen sollen bestimmt werden:
y = 2x2
2x2 = 0
x2 = 0
x1 = 0
x2 = 0
y = 4x2 + 4
4x + 4 = 0
4x2 = – 4
:2

2
Selbe Stelle
Wenn zweimal eine identische
Nullstelle errechnet wird, dann
handelt es sich um ein „doppelte
Nullstelle“, d.h., dass die Funktion
die x-Achse in einem Punkt
berührt (bei 0; 0).
y = 8x2 – 8
8x – 8 = 0
8x2 = + 8
-4
:4
2

x2 = – 1
Nicht möglich!
Eine Wurzel aus einer negativen
Zahl kann man nicht ziehen,
daher hat diese Funktion keine
Nullstelle.
+8
:8
x2 = + 1

x1 = + 1
x2 = – 1
Diese Funktion hat zwei
Nullstellen. Bei x1 = + 1 und bei
x2 = - 1. Immer daran denken,
dass die Wurzel einer Zahl immer
zwei Ergebnisse liefern kann.
Bei Funktionen in der Form „ax2 + bx + c“ sieht es jedoch etwas komplizierter aus und wir benötigen die so
genannte p,q-Formel:
Nullstellen von quadratischen Funktionen:
y = x2 + px + q
2
Mit dieser Formel können wir die Nullstellen von Funktionen in der Form „ax + bx + c“ berechnen. Vorher
2
müssen wir die Funktion aber in die Form „x + px + q“ bringen. Das ist nicht schwierig, denn wir müssen
einfach nur das „a“ vor dem „x2“ durch Division wegnehmen. Unser „p“ ist dann die Zahl, die nach der
Division vor dem „x“ steht und unser „q“ ist die Zahl, die nach der Division hinten ist. „x1;2“ bedeutet nur, dass
wir mit dieser Formel zwei Nullstellen berechnen, nämlich einmal „Plus Wurzel aus …“ und einmal „Minus
Wurzel aus…“. Das Minuszeichen vor „p/2“ bzw. vor dem „q“ bezieht sich darauf, dass die Funktion auch die
Form „x2 + px + q“ hat. Würde es „x2 – px – q“ heißen, würde es „+ p/2“ und „+ q“ heißen. Du musst mit
dieser Formel also immer die Vorzeichen wechseln. Beispiele: Die Nullstellen folgender Funktionen sollen
bestimmt werden:
y = x2 + 2x – 3
x2 + 2x – 3 = 0
 p=+2 ; q=–3
y = 4x2 – 8x – 5
x2 – 2x – 1,25 = 0
2
x1;2  
x1;2 =
x1;2 =
x1 =
x2 =




2
2
   3
2
2
1  4
1 2
1+2
 x1 = 1
1–2
 x2 = – 3
:4
 p = – 2 ; q = – 1,25
2
x1;2 
x1;2 =
x1;2 =
x1 =
x2 =
2
2
    1,25
2
2
1  2,25
1  1,5
1 + 1,5
 x1 = 2,5
1 – 1,5
 x2 = – 0,5
Auch hier gilt wieder: Erhält man für x1 und x2 identische Zahlen, so hat die Funktion nur eine Nullstelle. Und
müsste man aus einer negativen Zahl die Wurzel ziehen, so hat die Funktion keine Nullstelle.