doc-Format - Evangelische Friedrich Oberlin Fachoberschule

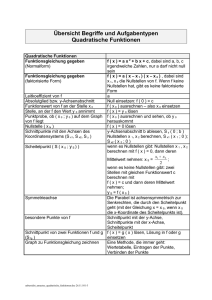
Evangelische Friedrich Oberlin Fachoberschule für
Sozialwesen, Wirtschaft, Verwaltung und Rechtspflege
Vorbereitungskurs 12 / 3. Runde:
Nullstellen
10. August 2005
Nullstellen
Helsinki. Ralf Bartels hat den Bann für die deutschen
Leichtathleten am ersten Tag der Weltmeisterschaft in
Helsinki gebrochen. Mit 20,99 Metern schaffte Bartels am
Samstagabend die Bronzemedaille im Kugelstoßen.
Damit hat der gute Mann nicht nur den größten Erfolg in seiner
Karriere erreicht, sondern uns gleichzeitig eine Steilvorlage für
unser neues Thema geliefert. Weshalb? Nun diese Frage
beantwortet das Aufgabenblatt zur Nullstellenberechnung.
Nullstellenberechnungen kommen in der Mathematik und insbesondere in Analysis recht häufig vor. Dabei
geht es dann immer um die Bestimmung derjenigen x-Werte, welche die Gleichung f  x   0 erfüllen. Auch
anschaulich ist eine Nullstelle (eine Stelle ist übrigens immer ein x-Wert auch Abszisse genannt) ein
markanter Punkt: In einer Nullstelle schneidet bzw. berührt ein Graph nämlich die x-Achse.
Nun müssen wir das alles mal auf sichere mathematische Füße stellen, d.h. es wird Zeit für eine Definition:
Eine Zahl x0 D heißt NULLSTELLE einer Funktion f, wenn gilt: f  x0   0
Lässt sich eine Funktion f in der Form f  x    x  x0   r  x  darstellen, wobei r  x  ein sog.
Restpolynom ist, so heißt x0 k-fache Nullstelle von f.
k
Beispiel:
1.
g  x   mx  t
2.
f  x   x2  x  6
3.
f  x    x  2  x  6
2

Es gilt: g  x0   0

mx0  t  0

Es gilt: f  x0   0

 x  2   x  3  0

2

Es gilt: f  x0   0
t
m
x1  2 x2  3
x0 
 x1  2 einzige und doppelte Nullstelle,
r  x
denn das Restpolynom r  x  hat in diesem Fall keine Nullstellen
Bemerkungen:
1. Die Vielfachheit einer Nullstelle x0 gibt an, wie der Graph einer Funktion in der Nähe der Nullstelle
verläuft:
- Ist k ungerade, dann wechselt das Vorzeichen von f x  bei x0 . G f wechselt bei x0 auf die andere
Seite der x-Achse.
- Ist k gerade, dann wechselt das Vorzeichen von f x  bei x0 nicht. G f bleibt bei x0 auf der
gleichen Seite der x-Achse.
- Je größer k ist, desto mehr schmiegt sich G f bei x0 an die x-Achse an.
Mehrfache Nullstellen und ihre graphische Auswirkung (Beispiele zum Herunterladen)
2. Kennt man die Nullstellen und ihre Vielfachheiten sowie das Vorzeichen von f  x  an einer Stelle (am
einfachsten für x  0 ), so lässt sich der Verlauf des Graphen im Groben beschreiben.
Beispiel:
f  x   161   x  2    x  1   x  3
2
3
Nullstellen bei x0  2 doppelt
x03,4,5  1 dreifach
1,2
Vorzeichen:
f  0  34  0
Vorzeichen
Skizzierter Kurvenverlauf mit bestimmt die Lage
des Graphen,
Vorzeichenübersicht:
x06  3 einfach
tatsächlicher Kurvenverlauf:
hier:
oberhalb der
x-Achse
+
+
-
-2
+
3
1
doppelt NSt.
dreif. NSt.
einf. NSt.
Kein Vorz.- Vorz.-Wechsel Vorz.-Wechsel
Wechsel
Lösungsverfahren zur Nullstellenberechnung
Bei den meisten Funktionen lassen sich die Nullstellen allerdings nicht so einfach erkennen wie in obigem
Beispiel. Deshalb gibt es verschiedene Lösungsverfahren zur Nullstellenberechnung:
1. Lineare Gleichungen
Jede lineare Gleichung lässt sich auf die Form
T1  x  T2
bringen, wobei T1 und T2 Terme sind, die die Gleichungsvariable x nicht mehr enthalten.
Die Lösungsmenge der Gleichung hängt von der Existenz des Quotienten
Fallunterscheidung durchzuführen.

kx  x  1 
Beispiel: kx  1  x  2
1. Fall: k  1 : Einsetzen liefert: 0  x  1  0  1
2. Fall: k  1 : Nun kann geteilt werden: x  
T2
T1
ab. Gegebenenfalls ist eine
 k 1 x  1
L  
1
, die Lösung ist also abhängig von k.
k 1
2. Quadratische Gleichungen
Jede quadratische Gleichung lässt sich auf die Form ax 2  bx  c  0 (NORMALFORM) mit a  0
bringen. (Für b  0 , bzw. für c  0 erhält man Sonderfälle). Auf die Normalform kann immer die
Mitternachtsformel angewendet werden, allerdings gibt es oftmals einfachere oder elegantere
Lösungsmöglichkeiten (z.B. Ausklammern (Test) , Satz von Vieta, binomische Formeln mit (Test)…)
3. Gleichungen höheren Grades
Gleichungen dritten oder höhern Grades müssen in der Regel auch auf die Normalform (Polynomform)
an x n  an 1 x n 1  ...  a1 x  a0  0 mit an  0 gebracht werden, um dann ein Lösungsverfahren anzuwenden
(Polynomdivision, Substitution…). Allerdings führen diese Verfahren mitunter nicht mehr zum Ziel.
Als besonders schülerfreundlich erweist sich dabei das Horner-Schema:
Beispiel:
f  x   2 x 4  8x3  6 x 2  8x  8 wird ins HORNER-SCHEMA übertragen:
x0
1
1
2
2
2
2
2
2
2
8
6
8
4
0
6
0
8
0
8
8
0
8
0
hier alternativ: Mitternachtsformel x03 / 4 
 vermutete Nullstelle (Teiler des konst. Glieds (hier:  8)
 "abschreiben von oben"
mit
 "1  2   8  "
 "1   6   6"
usw.
  8  
 8 
22
2
 4 28
2
 "abschreiben von oben"
und 2. Zeile
 "  1  2   6  "
 "  1   8   0"
usw.
 f  x   2   x  1   x  1   x  2    x  2 
 2   x  1   x  1   x  2 
2
mit den Nullstellen: x0  1; 1; 2; 2
Ein „Ausstieg“ aus dem Horner-Schema ist jederzeit möglich und erweist sich insbesondere dann als
günstig, wenn man ein Polynom zweiten Grades als Restpolynom hat, denn dann können a, b und c für
die Mitternachtsformel direkt aus dem Schema abgelesen werden (s.o.).