Aufgabentypen - Mathebaustelle

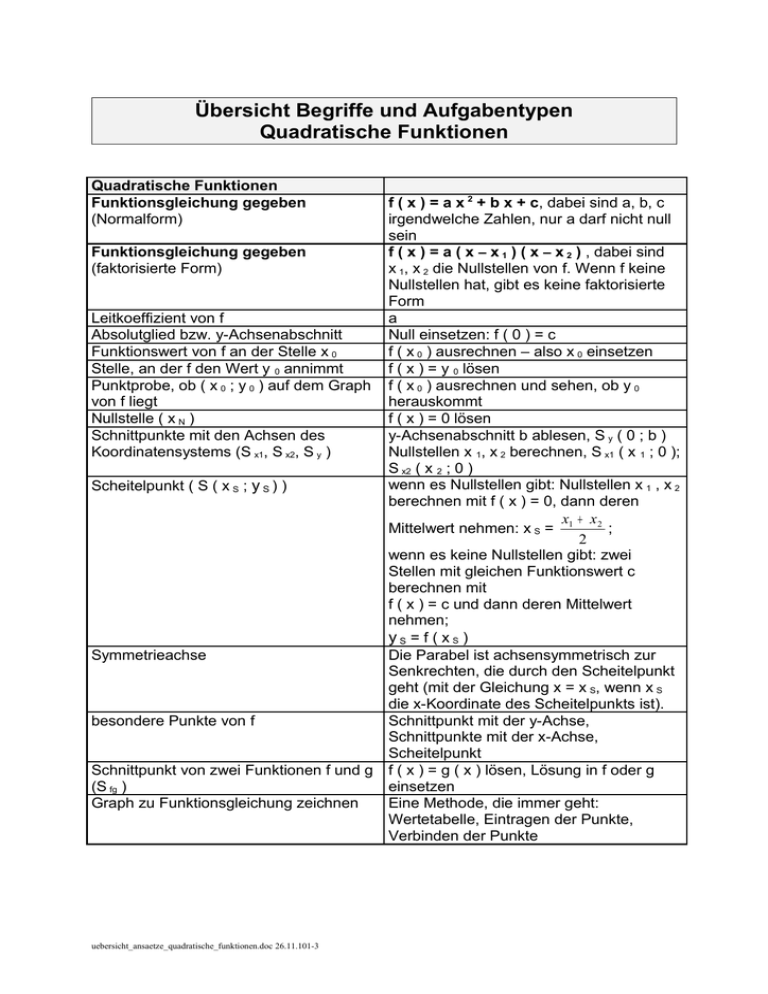
Übersicht Begriffe und Aufgabentypen
Quadratische Funktionen
Quadratische Funktionen
Funktionsgleichung gegeben
(Normalform)
f ( x ) = a x 2 + b x + c, dabei sind a, b, c
irgendwelche Zahlen, nur a darf nicht null
sein
Funktionsgleichung gegeben
f ( x ) = a ( x – x 1 ) ( x – x 2 ) , dabei sind
(faktorisierte Form)
x 1, x 2 die Nullstellen von f. Wenn f keine
Nullstellen hat, gibt es keine faktorisierte
Form
Leitkoeffizient von f
a
Absolutglied bzw. y-Achsenabschnitt
Null einsetzen: f ( 0 ) = c
Funktionswert von f an der Stelle x 0
f ( x 0 ) ausrechnen – also x 0 einsetzen
Stelle, an der f den Wert y 0 annimmt
f ( x ) = y 0 lösen
Punktprobe, ob ( x 0 ; y 0 ) auf dem Graph f ( x 0 ) ausrechnen und sehen, ob y 0
von f liegt
herauskommt
Nullstelle ( x N )
f ( x ) = 0 lösen
Schnittpunkte mit den Achsen des
y-Achsenabschnitt b ablesen, S y ( 0 ; b )
Koordinatensystems (S x1, S x2, S y )
Nullstellen x 1, x 2 berechnen, S x1 ( x 1 ; 0 );
S x2 ( x 2 ; 0 )
wenn es Nullstellen gibt: Nullstellen x 1 , x 2
Scheitelpunkt ( S ( x S ; y S ) )
berechnen mit f ( x ) = 0, dann deren
x + x2
Mittelwert nehmen: x S = 1
;
2
wenn es keine Nullstellen gibt: zwei
Stellen mit gleichen Funktionswert c
berechnen mit
f ( x ) = c und dann deren Mittelwert
nehmen;
yS = f ( xS )
Symmetrieachse
Die Parabel ist achsensymmetrisch zur
Senkrechten, die durch den Scheitelpunkt
geht (mit der Gleichung x = x S, wenn x S
die x-Koordinate des Scheitelpunkts ist).
besondere Punkte von f
Schnittpunkt mit der y-Achse,
Schnittpunkte mit der x-Achse,
Scheitelpunkt
Schnittpunkt von zwei Funktionen f und g f ( x ) = g ( x ) lösen, Lösung in f oder g
(S fg )
einsetzen
Graph zu Funktionsgleichung zeichnen
Eine Methode, die immer geht:
Wertetabelle, Eintragen der Punkte,
Verbinden der Punkte
uebersicht_ansaetze_quadratische_funktionen.doc 26.11.101-3
Eigenschaften / Teile der Funktionsgleichung aus Graph ablesen
Funktionsgleichung aufstellen
1. Fall: Normalform aufstellen aus
faktorisierter Form
2. Fall: Faktorisierte Form aufstellen aus
Normalform
y-Achsenabschnitt c: an Höhe des
Schnittpunkts mit der y-Achse ablesen
Leitkoeffizient a:
a < 0 ⇔ Parabel nach unten geöffnet,
a > 0 ⇔ Parabel nach unten geöffnet,
| a | (also: a ohne negatives Vorzeichen) =
1 ⇔ Normalparabel
| a | > 1 ⇔ gestreckte Parabel,
| a | < 1 ⇔ gestauchte Parabel
Nullstellen x 1 , x 2 ablesen führt direkt zur
faktorisierten Form („Vorzeichen
rumdrehen“)
Klammern ausmultiplizieren
Nullstellen x 1 und x 2 berechnen,
f ( x ) = a ( x – x1 ) ( x – x2 )
Www.mathebaustelle.de uebersicht_ansaetze_quadratische_funktionen.doc 26.11.102-3
Betriebswirtschaftliche Anwendungen
Preisabsatz-, Kosten-, Erlös- und
Gewinnfunktion
ökonomischer Definitionsbereich ( D
ök
)
Berechnung von E aus p
Berechnung von G aus E und K
Gewinnschwelle (x S, kleinere Nullstelle
von G) u. Gewinngrenze (x G, größere
Nullstelle von G)
Gewinnzone
Kosten (bzw. Erlös oder Gewinn/Verlust)
bei einer Ausbringungsmenge von x 0
M.E.
Ausbringungsmenge bei gegebenen
Kosten (bzw. Erlös oder Gewinn/Verlust)
von y 0 G.E.
erlösmaximale Ausbringungsmenge
maximaler Erlös
gewinnmaximale Ausbringungsmenge
( x max )
maximaler Gewinn
gewinnmaximaler Preis
Cournot´scher Punkt
( C ( x max ; p ( x max ) )
p ( x ) = m x + b (linear, wobei m < 0)
K ( x ) = k v x + K f (linear, k v: variable
Stückkosten, K f: Fixkosten,)
E ( x ) = x ⋅ p ( x ) = m x2 + b x
G(x)=E(x)–K(x)
Nullstelle von p berechnen: p ( x ) = 0, Das
b
Ergebnis ( x = –
) ist Obergrenze des
m
b
Definitionsbereichs: D ök = [ 0 ; –
]
m
E ( x ) = x ⋅ p ( x ) = m x2 + b x
G(x)=E(x)–K(x)
Nullstellen von G: G ( x ) = 0
(oder: E ( x ) = K ( x ))
Gewinnschwelle und -grenze x GS , x GG
berechnen; [ x GS ; x GG ]
K ( x0 )
(bzw. E ( x 0 ) oder G ( x 0 ))
K ( x ) = y 0 lösen
(bzw. E ( x ) = y 0
oder G ( x ) = y 0 )
x-Koordinate des Scheitelpunkts von E:
Mittelwert der Nullstellen von E
b
(Eine Nullstelle ist 0, die andere – , der
m
b
Mittelwert ist also
)
2m
erlösmaximale Ausbringungsmenge in E
b
einsetzen: E (
)
2m
x-Koordinate des Scheitelpunkts von G:
x + xGG
x max = GS
2
x max in G einsetzen: G ( x max )
x max in p einsetzen: p ( x max )
x-Koordinate: x max;
y-Koordinate: p ( x max )
C ( x max ; p ( x max ) )
Www.mathebaustelle.de uebersicht_ansaetze_quadratische_funktionen.doc 26.11.103-3