Quadratische Funktionen mit Parameter
Werbung

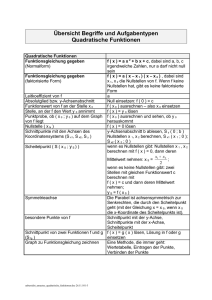
Evangelische Friedrich Oberlin Fachoberschule für Sozialwesen, Wirtschaft, Verwaltung und Rechtspflege Vorbereitungskurs 12 / 2. Runde: Quadratische Funktionen mit Parameter 3. August 2005 Quadratische Funktionen Das war eine prima Pizza letzte Woche, doch leider wurde die Freude darüber auf dem Heimweg schnell getrübt, denn leider kam es zu einem Unfall. Zum Glück sind Sie mit dem Auto nicht frontal auf den Vordermann aufgefahren, so dass allen Insassen nichts passiert ist, aber der Schaden am Auto war doch ganz erheblich. Aber was passiert eigentlich bei einem Frontalzusammenstoß? Das hängt natürlich ganz entscheidend von der Geschwindigkeit ab, wie aus der folgenden Tabelle zu erkennen ist: Geschwindigkeit v 36 72 108 144 in km/h Bremsbeschleunigung 100 400 900 1600 a in m/s2 Kraft F in N 7000 28000 63000 112000 Wie man schnell erkennt, ergibt sich bei einer Verdoppelung der Geschwindigkeit eine Vervierfachung der Bremsbeschleunigung bzw. der Kraft. Das deutet auf einen quadratischen Zusammenhang hin. Quadratische (und auch andere) Zusammenhänge drückt man in der Mathematik mit Hilfe einer Funktion aus. (Was ist eine Funktion?) In dieser Runde geht es speziell um die quadratischen Funktionen, also um Funktionen der Form p:x ax 2 bx c (Normalform). Der Term auf der rechten Seite des Abbildungspfeils sollte jedermann aus der Mitternachtsformel bekannt sein. Mit ihrer Hilfe berechnet man nämlich die Nullstellen einer solchen Funktion. Man löst also eine Gleichung der Form ax2 bx c 0 . Quadratischen Funktionen werden häufig mit einem p abgekürzt, weil ihr Graph eine Parabel ist. Wie diese Parabel aussieht, hängt natürlich ganz entscheidend von den Parameter a, b und c ab, wobei a, b und c reelle Zahlen sind und a natürlich ungleich 0 sein muss, da man sonst nur noch eine lineare Funktion hätte. Wie der Graph einer quadratischen Funktion aussieht, erkennt man am einfachsten an der so genannten 2 Scheitelform p : x a x xs ys . Diese kann durch Umformen aus der Normalform erzeugt werden (quadratische Ergänzung) und man stellt dann fest, dass das a dem a der Normalform entspricht (a ist der Streckungsfaktor) und xs und ys die Koordinaten des Scheitelpunktes darstellen. Der Scheitelpunkt lässt sich aber meist leichter mit Hilfe der einfachen Formel P xs b 2a 3 (Mitternachtsformel ohne die Wurzel) und durch Einsetzen des Skizze gefundenen Wertes in den Funktionsterm bestimmen. Mit Hilfe des 5 LE Streckungsfaktors a lässt sich dann jede Parabel sehr schnell in drei Schritten zeichnen: P2 1. Schritt: Scheitelpunkt berechnen oder (bei Scheitelform) ablesen 2. Schritt: weitere Punkte mit Hilfe des folgenden Schemas (vgl. Skizze) einzeichnen: 3 LE P1 Vom Scheitelpunkt S eine Längeneinheit nach rechts und eine nach oben neuer Punkt P1 1 LE Vom Punkt P1 eine Längeneinheit nach rechts und drei (immer S Länge 1 LE nächste ungerade Zahl) nach oben neuer Punkt P2 … Multipliziert man die Streckenlänge nach oben mit dem Streckungsfaktor a, so funktioniert dieses Schema für jede beliebige Parabel. Bei negativem a ist die Parabel natürlich nach unten geöffnet, d.h. man geht auch nach unten. 3. Schritt: Da jede Parabel achsensymmetrisch zu einer Parallelen zur y-Achse durch ihren Scheitelpunkt ist, macht man das Gleiche nach links und verbindet die erhaltenen Punkte. Quadratische Funktionen mit Parameter Gelegentlich betrachtet man auch mehrere quadratische Funktionen gleichzeitig, die alle ähnliche Eigenschaften haben. Mathematisch lässt sich so etwas mit Hilfe eines Parameters (z.B. k) erzeugen, d.h. man ersetzt in der Normalform nicht alle Parameter a, b und c durch Zahlen, um eine spezielle quadratische Funktion zu bekommen, sondern man lässt einen „frei“. So erhält man dann eine so genannte Funktionenschar. Diese kann auf ihre gemeinsamen Eigenschaften untersucht werden. Das geschieht jeweils in Abhängigkeit vom Parameter k. (Anmerkung: Das Gleiche macht man auch in der Abschlussprüfung, nur dass man dann eine Funktionenschar 3. oder 4. Grades untersucht!) Beispiel (an dem man sich auch gern selbst versuchen kann!): Gegeben ist die Funktion pk : x pk x D p R mit k pk x x 2kx 2 1 2 a) b) c) d) 2 k R Bestimme die Anzahl der Nullstellen der Funktion pk in Abhängigkeit von k! Bestimme für den Fall D 0 die Koordinaten des Scheitelpunkts S von pk Zeige, dass sich alle Funktionen pk in einem gemeinsamen Punkt schneiden! Zeichne die Graphen der Funktion pk für die Fälle k 1,5; 1; 0,5;0;0,5;1 und 1,5 in ein gemeinsames Koordinatensystem (Maßstab auf beiden Achsen: 1 LE 2 cm; 5 x 5 )! Lösung: Vorüberlegung: Die Anzahl der Nullstellen hängt von der Diskriminante D ab, den es gilt: D 0 2 (einfache) Nullstellen, D 0 1 (doppelte) NSt. (= Scheitelpunkt), D 0 keine NSt. a) D 2k 4 12 2 4k 2 4 , d.h. die Diskriminante ist selbst wieder eine quadratische Funktion (in 2 Abhängigkeit von k) mit dem Scheitelpunkt S 0 / 4 (Scheitelform!). Man bestimmt die Nullstellen (Mitternachtsformel oder Ausklammern und binomische Formel,…) k1 1 und k2 1 und folgert: D 0 für k1 1 und k2 1 : genau eine Nullstelle D 0 für k 1 k 1 : genau zwei Nullstellen (diese werden nicht extra angegeben) D 0 für 1 k 1 : keine Nullstellen k1 b) aus a) ergibt sich für k1 1 : x1/ 2 0 2 1 D 2 12 2 und yS 0 , da Nullstelle Mitternachtsformel und für k2 1 : x1/ 2 2 1 0 2 12 2 und ys 0 c) Um einen gemeinsamen Schnittpunkt bei einer Funktionenschar zu berechnen, nimmt man zwei beliebige Funktionen aus der Schar, z.B. pk1 und pk2 und setzt ihre Funktionsterme gleich ( k1 und k2 sind zwei beliebige Werte für k mit k1 k2 ): 1 2 x2 2k1x 2 12 x2 2k2 x 2 1 2 x2 2k2 x 2 : 2 k1x k2 x 0 x ausklammern k1 k2 x 0 k1 k2 wird nie 0, da k1 k2 x0 y 2 unabhängig von k , also ergibt sich der gemeinsame Schnittpunkt P 0 / 2 d) (es fehlt der Graph von p0,5 , da WinFunktion nur 6 Graphen zeichnen kann) Zur Überprüfung: Die Scheitelpunkte der Parabeln liegen alle auf der Parabel p : x 12 x2 2 . pk