Geraden- und Doppelkreuzungen

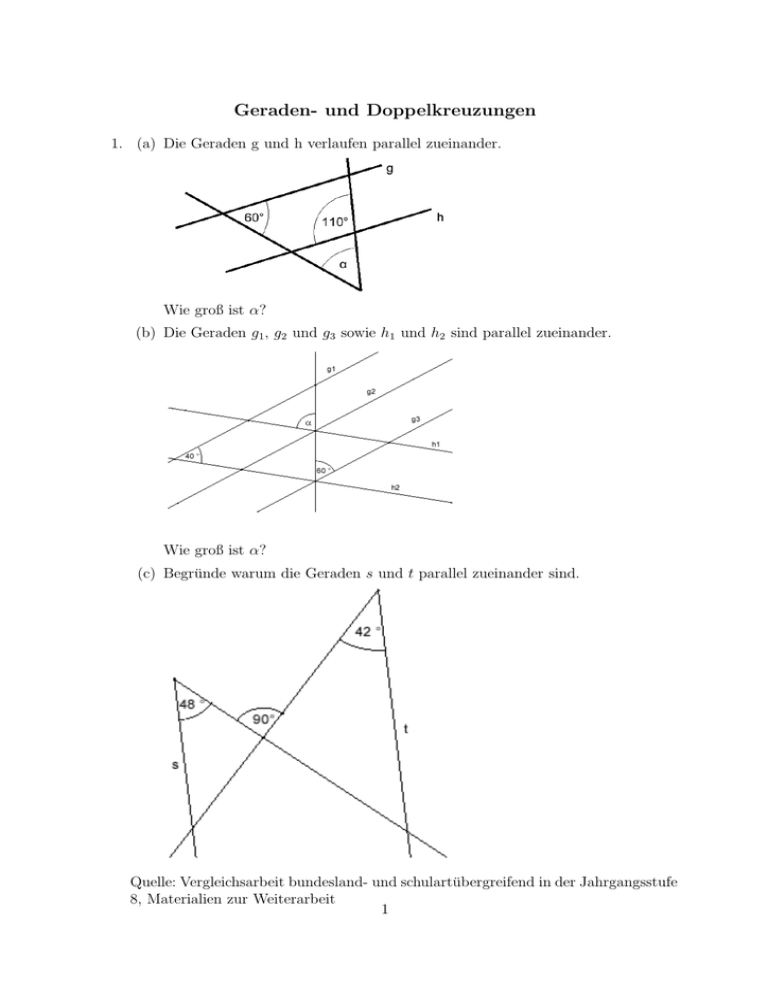
Geraden- und Doppelkreuzungen
1. (a) Die Geraden g und h verlaufen parallel zueinander.
Wie groß ist α?
(b) Die Geraden g1 , g2 und g3 sowie h1 und h2 sind parallel zueinander.
Wie groß ist α?
(c) Begründe warum die Geraden s und t parallel zueinander sind.
Quelle: Vergleichsarbeit bundesland- und schulartübergreifend in der Jahrgangsstufe
8, Materialien zur Weiterarbeit
1
Lösung: (a) 50◦ , (b) 80◦ , (c) Innenwinkel im rechten Dreieck sind 90◦ und 48◦ , daraus kann der
Winkel unten zu 42◦ berechnet werden, woraus die Parallelität wegen gleicher Z-Winkel
folgt.
2. Bestimme die mit griechischen Buchstaben gekennzeichneten Winkelmaße. Die nicht
maßstabsgetreue Zeichnung brauchst du nicht auf dein Blatt zu übertragen. Die
Geraden p1 und p2 sind parallel.
Begründe jeweils durch eine kurze Rechnung oder ein passendes Stichwort.
p1
ε
p
2
Lösung: α = 50◦
β = 40◦
130°
ϕ = 140◦
δ
β
α
ε = 50◦
ϕ
δ = 40◦
3. (a) An einer Doppelkreuzung entstehen die Wechselwinkel α = 65,5◦ und β =
50◦ 45′ . Berechne, unter welchen Winkeln sich die Geraden noch schneiden.
(b) In einem Dreieck ist α um 25◦ größer als β und γ ist dreimal so groß wie β.
Berechne alle Winkel des Dreiecks.
Lösung: (a) 114,5◦ , 129◦ 15′ , 14,75◦ ,
(b) α = 56◦ , β = 31◦ , γ = 93◦
165,25◦
4. Gegeben sind die Punkte A(−4| − 3), B(5|2), C(−2|2) und D(−6|4).
(a) Zeichne die Punkte in ein Koordinatensystem ein und ergänze die Gerade g =
AB, die Strecken [AC] und [CD].
Zeichne dann die Parallele h zur Geraden g durch den Punkt D. Trage die
Winkel α =<
) BAC, β =<
) DCA und γ =<
) ([CD], h) ein.
(b) Drücke den Winkel γ durch α und β aus.
(c) Suche andere Lösungswege zur Teilaufgabe (b)
2
Lösung: (a)
y
7
6
5
D
β
4
3
C
B
2
γ
1
x
0
−9
−8
−7
−6
−5
−4
−3
−2
0
−1
1
2
3
4
5
6
7
8
9
10
11
12
−1
−2
A
α
−3
−4
−5
(b)
• Lösung 1: α =<
) DCF, β =<
) FCA (Wechselwinkel an parallelen Geraden) =⇒
γ =<
) DCF+ <
) FCA = α + β
y
7
6
5
D
β
4
3
C
B
2
γ
1
F
x
0
−9
−8
−7
−6
−5
−4
−3
−2
0
−1
1
2
3
4
5
6
7
8
9
10
11
12
−1
−2
A
α
−3
−4
−5
• Lösung 2: δ = β (Wechselwinkel an parallelen Geraden) =⇒ γ = α + β (Außenwinkel im Dreieck)
3
y
8
F
δ7
6
5
D
β
4
3
C
B
2
γ
1
x
0
−9
−8
−7
−6
−5
−4
−3
−2
0
−1
1
2
3
4
5
6
7
8
9
10
11
−1
−2
A
α
−3
−4
• Lösung 3: δ = 90◦ − α, ǫ = 90◦ − β (Winkelsumme im Dreieck) =⇒ γ = 180◦ −
δ−ǫ=α+β
y
6
5
D
β
4
3
δ
C
B
2
γ
ǫ
1
x
0
− 10
−9
−8
−7
−6
−5
−4
−3
−2
0
−1
1
2
3
4
5
6
7
8
9
10
−1
−2
A
α
−3
−4
−5
−6
(c) vgl. (b)
5. Berechne alle eingezeichneten Winkel.
(a)
(b)
(c)
α
σ
o
β γ
40
α
δ
φ
β
γ
60
o
20
o
α
ε
γ
δ
4
β
11
Lösung: (a) α = β = γ = 90◦
(b) α = 60◦ , γ = 40◦ , β = δ = 80◦
(c) β = 20◦ , ε = α = ϕ = γ = 90◦ − 20◦ = 70◦
σ = δ = 90◦ − ϕ = 20◦
6. Berechne α, β, γ und δ, wenn
(a) β = 2α, γ = 2β und δ = 2γ
β
α
(b) β = 3α, γ = 23 β und δ = 43 γ
Lösung: (a) α + 2α + 4α + 8α = 15α = 180◦
=⇒
γ
δ
α = 12◦
β = 24◦ , γ = 48◦ und δ = 96◦
360 ◦
29
9
12 ◦
(b) α + 3α + α + 6α = α = 180◦ =⇒ α =
= 12
2
2
29
29
◦
◦
◦
25
14
7
, γ = 55
und δ = 74
β = 37
29
29
29
7. Welche Geradenpaare sind parallel?
e
70
o
65o
g
l
i
r
69 o
115
70
o
f
h
103,7
o
o
89,9 o
76,3 o
69
o
89,9 o
m
k
s
Lösung: e und f, g und h, l und m
8. Ein Winkel in nebenstehender Abbildung ist falsch, welcher könnte es sein?
Genaue Begründung deiner Antwort!
67 o
e
67
57 o
f
g
Lösung: Die beiden Winkel an der Geraden g müssen gleich sei.
5
123 o
o
67 o
h
57 o
k
9. Welche Geradenpaare sind parallel?
Genaue Begründung deiner Antworten!
r
e
88 o
46 o
88 o
92 o
f
92 o
h
Lösung: α = 180◦ − 92◦ = 88◦
=⇒ hkk (Stufenwinkel)
γ
92 o
g
42 o
i
s
k
r
e
88 o δ
β = 180◦ − 92◦ = 88◦
=⇒ ekf (Wechselwinkel)
88 o
α 92 o
β
f
γ = 180◦ − 92◦ − 42◦ = 46◦
=⇒ rks (Wechselwinkel)
46 o
92 o
h
6
γ
92 o
g
s
i
42 o
k