Ubungen zu den Winkelsätzen - ZUM-Wiki
Werbung
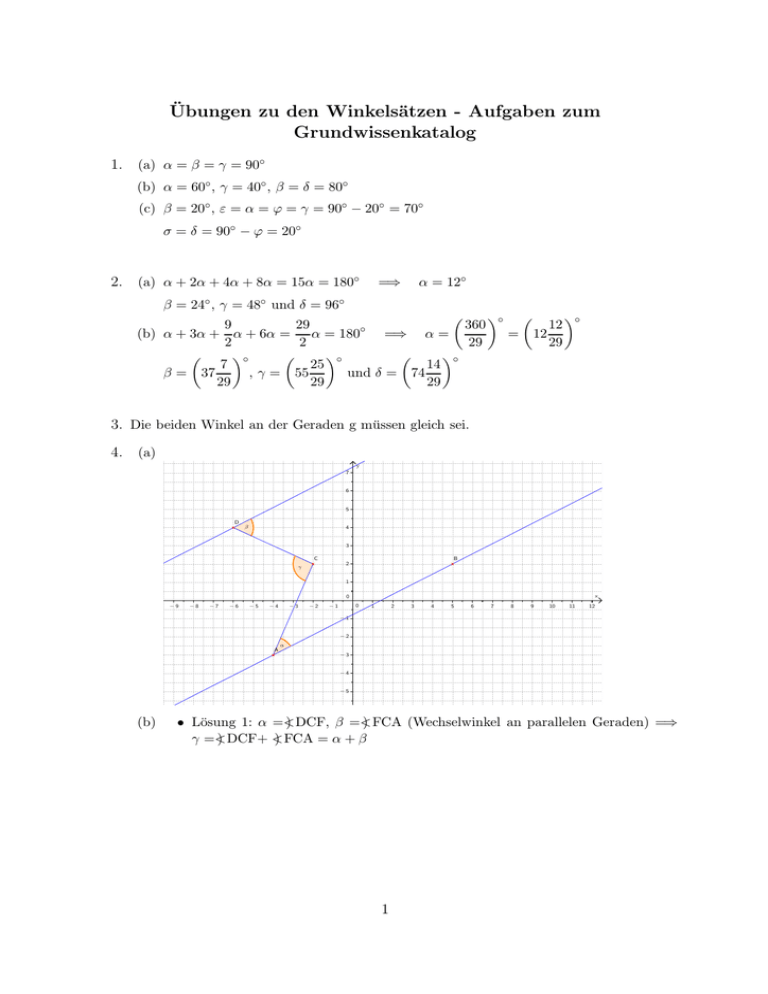
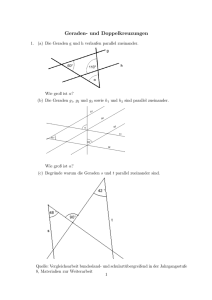
Übungen zu den Winkelsätzen - Aufgaben zum Grundwissenkatalog 1. (a) α = β = γ = 90◦ (b) α = 60◦ , γ = 40◦ , β = δ = 80◦ (c) β = 20◦ , ε = α = ϕ = γ = 90◦ − 20◦ = 70◦ σ = δ = 90◦ − ϕ = 20◦ 2. (a) α + 2α + 4α + 8α = 15α = 180◦ =⇒ α = 12◦ β = 24◦ , γ = 48◦ und δ = 96◦ 9 360 ◦ 29 12 ◦ ◦ (b) α + 3α + α + 6α = α = 180 =⇒ α = = 12 2 2 29 29 ◦ ◦ ◦ 25 14 7 , γ = 55 und δ = 74 β = 37 29 29 29 3. Die beiden Winkel an der Geraden g müssen gleich sei. 4. (a) y 7 6 5 D β 4 3 C B 2 γ 1 x 0 −9 −8 −7 −6 −5 −4 −3 −2 0 −1 1 2 3 4 5 6 7 8 9 10 11 12 −1 −2 A α −3 −4 −5 (b) • Lösung 1: α =< ) DCF, β =< ) FCA (Wechselwinkel an parallelen Geraden) =⇒ γ =< ) DCF+ < ) FCA = α + β 1 y 7 6 5 D β 4 3 C B 2 γ 1 F x 0 −9 −8 −7 −6 −5 −4 −3 −2 0 −1 1 2 3 4 5 6 7 8 9 10 11 12 −1 −2 A α −3 −4 −5 • Lösung 2: δ = β (Wechselwinkel an parallelen Geraden) =⇒ γ = α + β (Außenwinkel im Dreieck) y 8 F δ7 6 5 D β 4 3 C B 2 γ 1 x 0 −9 −8 −7 −6 −5 −4 −3 −2 0 −1 1 2 3 4 5 6 7 8 9 10 11 −1 −2 A α −3 −4 • Lösung 3: δ = 90◦ − α, ǫ = 90◦ − β (Winkelsumme im Dreieck) =⇒ γ = 180◦ − δ − ǫ = α + β 2 y 6 5 D β 4 3 δ C B 2 γ ǫ 1 x 0 − 10 −9 −8 −7 −6 −5 −4 −3 −2 0 −1 1 −1 −2 A α −3 −4 −5 −6 (c) vgl. (b) 5. α = 50◦ β = 40◦ ϕ = 140◦ ε = 50◦ δ = 40◦ 6. (a) (n − 2) · 180◦ (b) 144◦ 3 2 3 4 5 6 7 8 9 10 11