¨Ubungen zur Einführung in die Astronomie Anwesenheitsübungen III

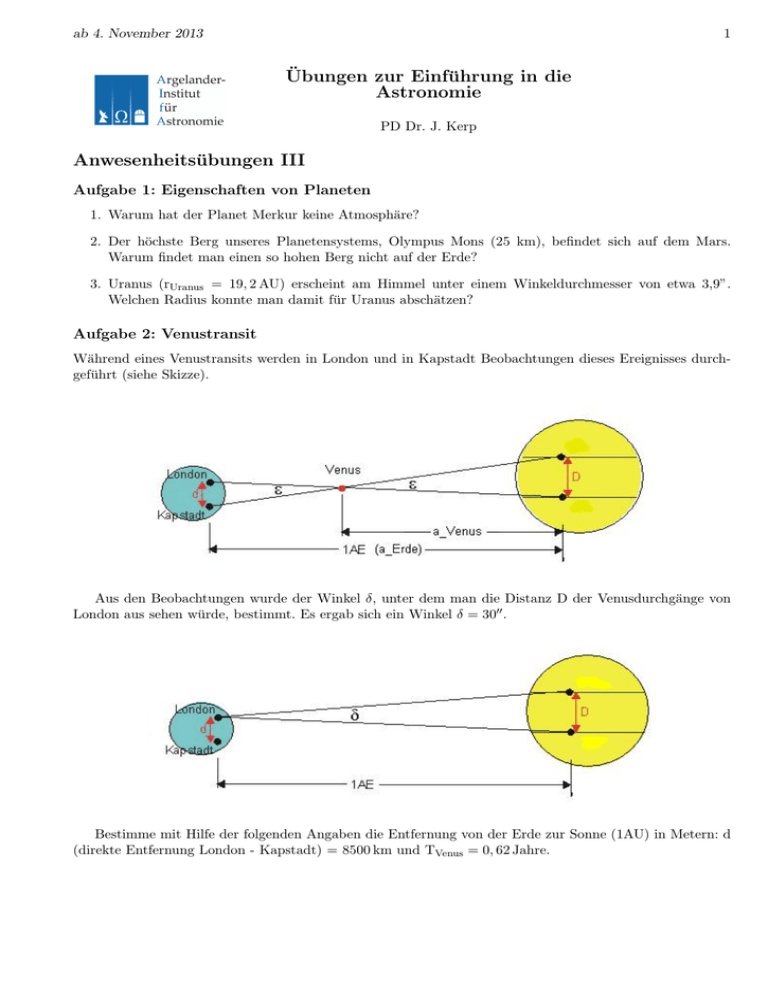
ab 4. November 2013
1
Übungen zur Einführung in die
Astronomie
PD Dr. J. Kerp
Anwesenheitsübungen III
Aufgabe 1: Eigenschaften von Planeten
1. Warum hat der Planet Merkur keine Atmosphäre?
2. Der höchste Berg unseres Planetensystems, Olympus Mons (25 km), befindet sich auf dem Mars.
Warum findet man einen so hohen Berg nicht auf der Erde?
3. Uranus (rUranus = 19, 2 AU) erscheint am Himmel unter einem Winkeldurchmesser von etwa 3,9”.
Welchen Radius konnte man damit für Uranus abschätzen?
Aufgabe 2: Venustransit
Während eines Venustransits werden in London und in Kapstadt Beobachtungen dieses Ereignisses durchgeführt (siehe Skizze).
Aus den Beobachtungen wurde der Winkel δ, unter dem man die Distanz D der Venusdurchgänge von
London aus sehen würde, bestimmt. Es ergab sich ein Winkel δ = 3000 .
Bestimme mit Hilfe der folgenden Angaben die Entfernung von der Erde zur Sonne (1AU) in Metern: d
(direkte Entfernung London - Kapstadt) = 8500 km und TVenus = 0, 62 Jahre.
2
Aufgabe 3: Parallaxe
1. Erkläre die jährliche Parallaxe durch eine Skizze.
2. Wie bestimmt man daraus die Entfernung eines Sterns?
3. Ein Stern habe die Parallaxe 0,1”. Berechne seine Entfernung.
Wie weit ist ein Stern mit doppelter Parallaxe entfernt?
4. Wie viele Meter sind 1 Ly (Lichtjahr) und 1 AE?
5. Vergleiche die Entfernungen zu folgenden Objekten in passenden Maßeinheiten:
Mond, Sonne, Saturn, Rand des Sonnensystems, nächster Stern
Aufgabe 4: Gravitationsgesetz und Keplersche Gesetze
1. Nenne das Newtonsche Gravitationsgesetz und die drei Keplerschen Gesetze.
2. Der Jupitermond Kallisto braucht zu einem Umlauf um den Planeten auf einer kreisförmigen Bahn (r
= 1, 88 · 106 km) 16 Tage und 17 Stunden. Berechne daraus die Jupitermasse.
3. Die Umlaufdauer von Neptun beträgt 165 Jahre. Berechne die Entfernung zu Neptun!
Zusatzaufgabe
1. Beobachten wir am 15. April 2014 die totale Mondfinsternis und messen dabei zwei Zeiträume. I) Die
Zeitspanne die der Mond vom ersten Kontakt“ bis zum vollständigen Eintritt in den Kernschatten
”
benötigt. II) Die Zeitspanne, die der Mond benötigt, um den Kernschatten der Erde einmal vollständig
zu durchqueren. Zeitraum I) beträgt 114 Minuten, Zeitraum II) 418 Minuten. Bestimme unter Nutzung
des bekannten Erdradius von 6400 km den Durchmesser des Mondes in km.
2. Mittels eines Jakobsstabes von 150 cm Länge wird festgestellt, dass eine Blende von 1,3 cm Höhe die
gleiche projezierte Größe wie der Mond am Himmel hat. I) Bestimme den Monddurchmesser durch diese
Messung in Einheiten von Bogenminuten. Unter Nutzung des aus (1) bekannten Monddurchmessers
bestimme die Entfernung zwischen Mond und Erde.