6 Folien/Seite - informatik.uni-bremen.de

Universität Bremen
Universität Bremen
Bäume 1
Rückblick „Sortieren“
Permutieren nach Dijkstra
2
4
Thomas Röfer
3
3
1
4
Sortieren durch …
… Einfügen
S = perm(T), s0 ≤ s1 ≤ ... ≤ sn-1
2
1
1 2
oder
3
5
S = perm(T), s0 ≥ s1 ≥ ... ≥ sn-1
Begriffsdefinitionen
Eigenschaften
Implementierung von Bäumen
Durchlaufen von Bäumen
Breitensuche/Tiefensuche
Huffman-Kodierung
… Auswählen
1 3
5
… Vertauschen
(BubbleSort)
2 3
2
1
4
4
… Mischen
1 2
3
4
Quicksort
7
4
1
9
0
2
5
4
8
3
7
4
1
3
0
2
5
4
8
9
4
4
1
3
0
2
5
7
8
9
5
5
2 5
1
3
4
quickSort
PI-2: Bäume 1
Universität Bremen
quickSort
2
Universität Bremen
Einleitung
Begriffe
Motivation
Knoten
Kann einen Namen haben (Etikett, Label) und/oder andere Informationen tragen
Kann mehrere untergeordnete Knoten haben (Kindknoten, Nachfolger)
Kann maximal einen übergeordneten Knoten haben (Elternknoten, Vorgänger)
Hat ein Knoten keinen übergeordneten Knoten, ist er die Wurzel des Baums
Der Verzweigungsgrad eines Knotens ist die Anzahl seiner Kindknoten
Hat ein Knoten keine Nachfolger, ist er ein Blatt (Terminalknoten)
Reihungen sind statisch bzw. nur teuer zu vergrößern
und zu verkleinern
Listen sind dynamisch, aber man kann in ihnen nur
linear suchen
Ansatz
Man kann Bäume als verallgemeinerte Listenstruktur
ansehen
Jeder Knoten hat nicht einen, sondern viele Nachfolger
Kante
Verbindet jeweils zwei Knoten (Eltern- mit Kindknoten)
Pfad
Beispiel
Folge von unterschiedlichen Knoten, wobei aufeinander folgende
Knoten durch Kanten verbunden sind
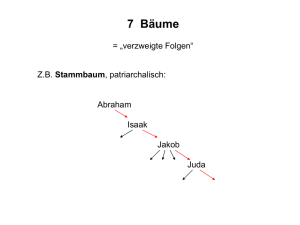
Z.B. Teile und Kapitel von „Algorithmen in Java“
Baum
Nichtleere Sammlung von Knoten und Kanten
Jeweils zwei Knoten sind genau durch einen Pfad verbunden
Mehrere nicht miteinander verbundene Bäume bezeichnet man als Wald
PI-2: Bäume 1
3
PI-2: Bäume 1
Universität Bremen
4
Universität Bremen
Begriffe
Begriffe
Ordnung eines Baums
ternärer Baum
Der maximale Verzweigungsgrad seiner Knoten
Binärbaum
binärer Baum
Die Ordnung des Baums ist 2
Geordneter Baum
Zwischen den Kindern der Knoten ist eine Ordnung definiert
z.B. erster, zweiter, dritter … Kindknoten
Tiefe eines Knotens
freier Baum
Der Abstand zwischen der Wurzel und dem Knoten (Anzahl
der Kanten)
Die Wurzel hat die Tiefe 0
Alle Knoten mit derselben Tiefe gehören zur selben Ebene
(zum selben Niveau)
Höhe eines Baums
Die maximale Tiefe eines Knotens im Baum
Wurzelbaum
PI-2: Bäume 1
5
PI-2: Bäume 1
6
1
Universität Bremen
Universität Bremen
Definitionen und Eigenschaften
Graphen und Bäume
Voller Baum
Andere Sichtweise
Ein Baum heißt voll, wenn der Verzweigungsgrad aller inneren
Knoten der Ordnung des Baums entspricht
Bäume können nicht nur als Verallgemeinerung
von Listen gesehen werden, sondern auch als
Spezialfall von Graphen
Vollständiger Baum
Baum mit gerichteten Kanten
Ein Baum heißt vollständig, wenn die Tiefe aller Blätter der
Höhe des Baums entspricht
Ein Baum mit gerichteten Kanten verhält sich in
seiner Implementierung analog zu einer einfach
verketteten Liste
Alle Kanten zeigen von Elternknoten zu
Kindknoten
Ein Baum mit n Knoten hat n-1 Kanten
Zu jedem Knoten führt eine Kante, nur zur Wurzel nicht
Ein vollständiger Binärbaum der Höhe n hat 2n Blätter
Ein Binärbaum, der nur aus der Wurzel besteht, hat ein Blatt
Ein vollständiger Binärbaum der Höhe n+1 hat doppelt so viele Blätter
wie einer der Höhe n
Baum mit ungerichteten Kanten
Ein Baum mit ungerichteten Kanten verhält sich
in seiner Implementierung analog zu einer
doppelt verketteten Liste
Kindknoten haben zusätzlich einen Verweis auf
ihren Elternknoten
Ein vollständiger Binärbaum der Höhe n hat 2n+1 – 1 Knoten
Ein Binärbaum, der nur aus der Wurzel besteht, hat einen Knoten
Mit jeder Ebene kommt ein Knoten mehr hinzu, als schon im Baum
vorhanden sind: knoten(n+1) = 2 × knoten(n) + 1
PI-2: Bäume 1
7
Universität Bremen
PI-2: Bäume 1
8
Universität Bremen
Implementierung von Bäumen
Knoten
Implementierung eines Binärbaums
class
class Node
Node
{{
Node
Node left,
left,
right;
right;
Object
Object data;
data;
Binärbaum
Node(Object
Node(Object o,
o, Node
Node l,
l, Node
Node r)
r)
{{
data
data == o;
o;
left
=
l;
left = l;
right
right == r;
r;
}}
Baum
}}
class
class Tree
Tree
{{
private
private Node
Node root;
root;
Tree(Node
Tree(Node n)
n)
{{
root
root == n;
n;
}}
boolean
boolean isLeaf()
isLeaf()
{{
return
return left
left ==
== null
null &&
&&
right
right ==
== null;
null;
}}
}}
PI-2: Bäume 1
9
Universität Bremen
Die Knoten eines Baums können in
verschiedenen Reihenfolgen
durchlaufen werden
Beim Durchlaufen können
Operationen auf den in den Knoten
enthaltenen Daten durchgeführt
werden
Mögliche Reihenfolgen
Präorder-Sequenz
Postorder-Sequenz
Inorder-Sequenz
Level-Order-Sequenz
PI-2: Bäume 1
boolean
boolean isEmpty()
isEmpty()
{{
return
return root
root ==
== null;
null;
}}
10
Universität Bremen
Durchlaufen eines Baums
Ansatz
PI-2: Bäume 1
boolean
boolean isInnerNode()
isInnerNode()
{{
return
return !isLeaf();
!isLeaf();
}}
Präorder-Sequenz
interface
interface NodeAction
NodeAction
{{
void
action(Node
void action(Node n);
n);
}}
class
class NodePrintAction
NodePrintAction
implements
implements NodeAction
NodeAction
{{
public
void
public void action(Node
action(Node n)
n)
{{
System.out.print(
System.out.print(
n.data.toString()
n.data.toString() ++ "" ");
");
}}
}}
11
Ansatz
In jedem Knoten wird
zuerst der Knoten
verarbeitet, dann die
Kindknoten
Beispiel
+1*23
PI-2: Bäume 1
void
void preorder(NodeAction
preorder(NodeAction a)
a)
{{
if(!isEmpty())
if(!isEmpty())
{{
a.action(root);
a.action(root);
new
new Tree(root.left)
Tree(root.left)
.preorder(a);
.preorder(a);
new
new Tree(root.right)
Tree(root.right)
.preorder(a);
.preorder(a);
}}
}}
12
2
Universität Bremen
Universität Bremen
Postorder-Sequenz
Inorder-Sequenz
Ansatz
Ansatz
In jedem Knoten werden
zuerst die Kindknoten
verarbeitet, dann der
Knoten selbst
Beispiel
123*+
void
void postorder(NodeAction
postorder(NodeAction a)
a)
{{
if(!isEmpty())
if(!isEmpty())
{{
new
new Tree(root.left)
Tree(root.left)
.postorder(a);
.postorder(a);
new
new Tree(root.right)
Tree(root.right)
.postorder(a);
.postorder(a);
a.action(root);
a.action(root);
}}
}}
PI-2: Bäume 1
13
Universität Bremen
Statt Rekursion wird ein Stapel
verwendet, um die offenen Knoten
zu speichern
Der Stapel ist vom Typ last-in-firstout
Hinweis
Kann ebenfalls für Postorder- und
Inorder-Sequenz genutzt werden
PI-2: Bäume 1
1+2*3
PI-2: Bäume 1
14
Level-Order-Sequenz
void
void preorder(NodeAction
preorder(NodeAction a)
a)
{{
Stack
Stack stack
stack == new
new Stack();
Stack();
stack.push(root);
stack.push(root);
while(!stack.isEmpty())
while(!stack.isEmpty())
{{
Node
Node node
node == (Node)
(Node) stack.pop();
stack.pop();
if(node
if(node !=
!= null)
null)
{{
a.action(node);
a.action(node);
stack.push(node.right);
stack.push(node.right);
stack.push(node.left);
stack.push(node.left);
}}
}}
}}
15
Universität Bremen
Ansatz
Die Knoten werden ihrer Ebene
nach durchlaufen und
innerhalb jeder Ebene
von links nach rechts
Nutzung eines
first-in-first-out Stapels
(Warteschlange)
Beispiel
+1*23
void
void levelOrder(NodeAction
levelOrder(NodeAction a)
a)
{{
Queue
Queue stack
stack == new
new Queue();
Queue();
stack.push(root);
stack.push(root);
while(!stack.isEmpty())
while(!stack.isEmpty())
{{
Node
Node node
node == (Node)
(Node) stack.pop();
stack.pop();
if(node
if(node !=
!= null)
null)
{{
a.action(node);
a.action(node);
stack.push(node.left);
stack.push(node.left);
stack.push(node.right);
stack.push(node.right);
}}
}}
}}
PI-2: Bäume 1
16
Universität Bremen
Spielprobleme
Spielprobleme – Tiefen-/Breitensuche
Spielprobleme
Tiefensuche
Bei Spielproblemen (z.B. Schach) werden mögliche Zugfolgen durchprobiert
und das Ergebnis bewertet
Dabei wird unter allen eigenen Zügen der mit der besten Bewertung gesucht
(Bewertung maximieren)
Allerdings muss man davon ausgehen, dass der Gegner den für einen selbst
ungünstigsten Zug auswählen wird (Bewertung minimieren)
Daher spricht man dabei von einem Mini-Max-Problem
Eigene Züge
Durchsuche den Baum der möglichen Zugfolgen
bis zu einer bestimmten Tiefe
Verwende den besten gefundenen Zug
Breitensuche
Durchsuche den Baum der möglichen Zugfolgen
in Level-Order-Reihenfolge so lange, bis die Zeit
um ist
Verwende den besten gefundenen Zug
Inkrementelle Tiefensuche
Gegnerische Züge
Durchsuche den Baum der möglichen Zugfolgen
bis zu einer bestimmten Tiefe
Ist noch Zeit übrig, erhöhe die Tiefe um 1 und
beginne von vorne
Verwende den besten gefundenen Zug
Eigene Züge
Gegnerische Züge
Eigene Züge
PI-2: Bäume 1
Beispiel
void
void inorder(NodeAction
inorder(NodeAction a)
a)
{{
if(!isEmpty())
if(!isEmpty())
{{
new
new Tree(root.left)
Tree(root.left)
.inorder(a);
.inorder(a);
a.action(root);
a.action(root);
new
new Tree(root.right)
Tree(root.right)
.postorder(a);
.postorder(a);
}}
}}
Universität Bremen
Präorder-Sequenz ohne Rekursion
Ansatz
In jedem Knoten wird zuerst
der linke Kindknoten
verarbeitet, dann der Knoten
selbst, dann der rechte
Kindknoten
Funktioniert nur bei
Binärbäumen
17
PI-2: Bäume 1
18
3
Universität Bremen
Universität Bremen
Huffman Komprimierung
Aufbau eines Huffman-Baumes
Kodierung mit fester Bitanzahl
Gegeben sei eine leere Liste von Binärbäumen
Für jedes Zeichen
A: 000 C: 010 E: 100
G: 110
B: 001 D: 011 F: 101
H: 111
BACADAEAFABBAAAGAH wird mit 18 × 3 = 54 Bits kodiert:
001 000 010 000 011 000 100 000 101 000 001 001 000 000 000 110 000 111
Ansatz
Wenn Zeichen in einem Text unterschiedlich häufig vorkommen, wäre es günstig, die
häufigeren mit weniger Bits zu kodieren und die seltenen mit mehr
Kodierung mit variabler Bitanzahl
Probleme
Wenn Zeichen durch unterschiedlich viele Bits repräsentiert werden, muss man
erkennen können, wo ein Zeichen endet und wo das nächste beginnt
Zudem braucht man ein Lexikon, in dem steht, welche Bitfolge welchem Zeichen
entspricht
Der letzte in der Liste verbliebene Binärbaum ist der Huffman-Baum
19
PI-2: Bäume 1
Universität Bremen
1
1
1
1
1
1
3
9
D
C
F
E
H
G
B
A
1
1
1
1
3
9
F
E
H
G
B
A
1
1
H
G
PI-2: Bäume 1
1
1
D
C
2
2
1
1
1
1
F
E
D
C
20
Universität Bremen
Beispiel: BACADAEAFABBAAAGAH
2
Solange die Liste mehr als einen Baum enthält
Entnimm die beiden ersten Elemente aus der Liste
Erzeuge einen neuen Binärbaum, bei dem der linke Kindknoten der ursprünglich erste
Baum in der Liste ist und der rechte Kindknoten der ursprünglich zweite Baum
Die in der Wurzel vermerkte Häufigkeit ist die Summe der Häufigkeiten der beiden
Teilbäume
Füge den Baum aufsteigend nach der in der Wurzel vermerkten Häufigkeit sortiert in die
Liste ein
A: 0
C: 1010 E: 1100 G: 1110
B: 100 D: 1011 F: 1101 H: 1111
BACADAEAFABBAAAGAH wird mit 42 Bits kodiert:
100 0 1010 0 1011 0 1100 0 1101 0 100 100 0 0 0 1110 0 1111
PI-2: Bäume 1
Erzeuge einen Binärbaum, bei dem die Wurzel ein Blatt ist und das Zeichen und seine
Häufigkeit enthält.
Füge den Baum aufsteigend nach der in der Wurzel vermerkten Häufigkeit sortiert in die
Liste ein
3
9
B
A
2
2
Beispiel: BACADAEAFABBAAAGAH
2
1
1
1
1
1
1
H
G
F
E
D
C
3
2
1
1
D
C
3
9
B
A
9
4
B
2
A
2
1
1
1
1
H
G
F
E
4
5
2
2
1
1
1
1
H
G
F
E
D
1
Durch Pfad von der Wurzel zum
Zeichen
Wenn nach rechts verzweigt wird,
schreibe eine 0
Wenn nach links verzweigt wird,
schreibe eine 1
2
3
2
1
1
1
1
1
H
G
F
E
D
C
1
9
1
4
B
0
18
9
0
1 5
0
0
A
1 2 0 1 2 01 2 0 3
1 1 1 1 1 1 B
B
C
21
2
1
A
5
1
C: links, rechts, links rechts
1010
A
9
4
Beispiel
9
3
2
1
9
Eigentliche Kodierung
H
PI-2: Bäume 1
G
F
E
D
C
22
4