Mittelsenkrechte, Lot

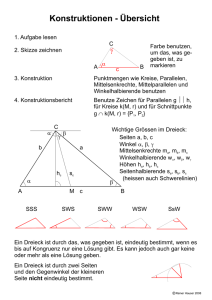
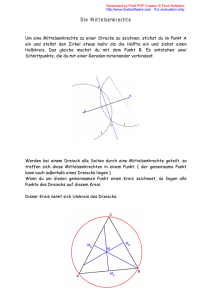
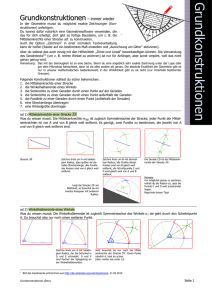
Mittelsenkrechte, Lot
1. (a) Gegeben sind zwei verschiedene Punkte P und Q. Gesucht sind alle Geraden,
von denen P und Q gleichen Abstand haben.
(b) Gegeben sind drei verschiedene Punkte P,Q und R. Gesucht sind alle Geraden,
von denen P, Q und R gleichen Abstand haben.
(c) Gegeben sind zwei verschiedene Punkte P und Q. Gesucht sind alle Kreise, von
denen P und Q gleichen Abstand haben.
Lösung: (a) Gerade PQ, Parallelen zu PQ, Mittelsenkrechte der STrecke [PQ] und Geraden durch
den Mittelpunkt M der Strecke [PQ]
(b) 1. Fall: P,Q,R liegen auf einer Geraden ⇒ Gerade PQ und Parallelen zu PQ
2. Fall: P, Q und R nicht auf einer Geraden ⇒ Mittelparallelen des Dreiecks △P QR
(c) Der Abstand eines Punktes von einem Kreis ist das Minimum aller Entfernungen
zwischen diesem Punkt und einem Punkt des Kreises.
Kreise um Mittelpunkt der Strecke [PQ] liegt mit beliebigem Radius und Kreise um
beliebigem Punkt M mit Radius r = 21 (P M + QM )
2. Nenne 2 Eigenschaften eines Dreiecks, bei dem eine Höhe gleichzeitig Mittelsenkrechte ist.
Quelle: Jufo go (Spiel zum Wettbewerb Jugend forscht)
Lösung: 2 gleichlange Seiten, zwei gleichgroße Winkel, achsensymmetrisch; es handelt sich um ein
gleichschenkliges Dreieck.
3. Die gehfaulen Ameisen
Die gemütliche Anatevka and die dicke Berta stehen 50 mm voneinander entfernt.
Sie wollen sich zwar treffen, aber keine will weiter als 28 mm laufen.
(a) Kennzeichne das Gebiet ihrer möglichen Treffpunkte!
(b) Wie weit müssten sie voneinander entfernt sein, damit es nur einen einzigen
Treffpunkt gibt?
Lösung: (a) Kreise um Anatevka und Berta mit Radius 28 mm schneiden sich in zwei Punkte P1
und P2 der Mittelsenkrechten von Anatevka und Berta. Die Punkte der Strecke [P1 P2 ]
sind die möglichen Treffpunkte.
(b) 56 mm
4. Die gehfaulen Ameisen
Anatevka und Berta sind für Gehgerechtigkeit und achten deshalb genau darauf,
dass keine weiter als die andere krabbeln muss, egal wie weit, Hauptsache beide
gleich weit.
Zeichne ihre möglichen Treffpunkte ein!
1
Lösung: Mittelsenkrechte auf AB, Pfütze berücksichtigen!
2