ganze Zahlen - Touchdown Mathe
Werbung
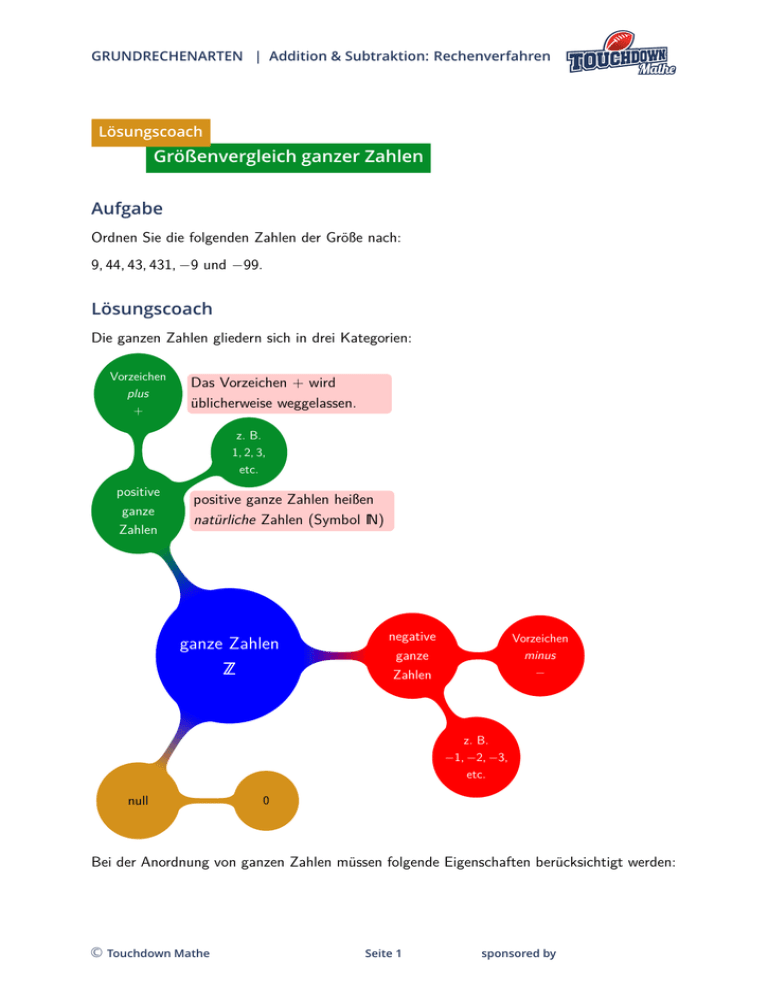
GRUNDRECHENARTEN | Addition & Subtraktion: Rechenverfahren Lösungscoach Größenvergleich ganzer Zahlen Aufgabe Ordnen Sie die folgenden Zahlen der Größe nach: 9, 44, 43, 431, −9 und −99. Lösungscoach Die ganzen Zahlen gliedern sich in drei Kategorien: Vorzeichen plus + Das Vorzeichen + wird üblicherweise weggelassen. z. B. 1, 2, 3, etc. positive ganze Zahlen positive ganze Zahlen heißen natürliche Zahlen (Symbol IN) N ganze Zahlen Z negative ganze Zahlen Vorzeichen minus − z. B. −1, −2, −3, etc. null 0 Bei der Anordnung von ganzen Zahlen müssen folgende Eigenschaften berücksichtigt werden: © Touchdown Mathe Seite 1 sponsored by GRUNDRECHENARTEN | Addition & Subtraktion: Rechenverfahren 1. das Vorzeichen, 2. die Anzahl der Stellen und 3. die Ziffernfolge. Es gelten die folgenden drei Ordnungskriterien: 1. Zahlen mit negativem Vorzeichen (−) sind immer kleiner als Zahlen mit positivem Vorzeichen (+). 2. Bei positiven ganzen Zahlen gilt: je mehr Stellen die Zahl hat, desto größer ist sie. Bei negativen Zahlen ist es umgekehrt. 3. Haben zwei ganze Zahlen dasselbe Vorzeichen und dieselbe Stellenzahl, so müssen sie Ziffer für Ziffer von links nach rechts verglichen werden: ist die 1. Ziffer bei einer Zahl größer, dann ist das die größere Zahl; ist die 1. Ziffer bei beiden gleich, so betrachte man jeweils die 2. Ziffer. Wenn beide Zahlen auch dieselbe 2. Ziffer haben, dann betrachte man jeweils die 3. Ziffer, usw. Man muss ganze Zahlen ordnen können, um schriftlich zu subtrahieren und dann auch Brüche und Dezimalzahlen ordnen zu können. Die Aussage „drei ist weniger als sechs“ wird als Formel so geschrieben: 3 < 6, sprich „drei kleiner 6“. Dabei ist „<“ das Kleiner-Zeichen. Es gibt auch ein entsprechendes „größer“-Zeichen: 5 > 4 (sprich: „5 größer 4“) bedeutet „fünf ist mehr als vier“. Die Anordnung der ganzen Zahlen kann mit Hilfe einer Zahlengerade veranschaulicht werden. Der Pfeil gibt die Richtung von klein nach groß an: ... ... −4 −3 −2 −1 0 1 2 3 4 negativ positiv Schritt 1: Zahlen nach Vorzeichen sortieren Nach der 1. Regel sind die negativen Zahlen die kleinsten, d. h. jede Zahl im linken Kasten ist kleiner als jede andere Zahl im rechten Kasten: © Touchdown Mathe Seite 2 sponsored by GRUNDRECHENARTEN | Addition & Subtraktion: Rechenverfahren 9 −9 −99 44 < 43 431 negativ positiv Schritt 2: Zahlen nach Stellenzahl sortieren Um die Zahlen im linken Kasten zu ordnen, wenden wir die 2. Regel an: −99 hat eine Stelle mehr als −9. Negativen Zahlen sind umso kleiner, je mehr Stellen sie haben. Also ist −99 kleiner als −9. Nun zum rechten Kasten: 9 hat weniger Stellen als 44 und 43, diese wiederum weniger als 431. Wir erhalten somit folgende Ordnung: −99 < −9 < 9 44 43 < 1-stellig < 2-stellig negativ 431 3-stellig positiv Schritt 3: Zahlen nach Ziffernfolge sortieren Jetzt bleiben nur noch zwei Zahlen, die wir in die richtige Reihenfolge bringen müssen: 44 und 43. Diese müssen wir Ziffer für Ziffer vergleichen. 1. Ziffer: 44 und 43 haben beide die 4 als erste Ziffer, also müssen wir die 2. Ziffer betrachten. 2. Ziffer: 44 hat als 2. Ziffer 4 und 43 hat als 2. Ziffer 3. Es ist 4 > 3, also ist 44 > 43. Somit ergibt sich folgende Ordnung: −99 < −9 < 9 < 1-stellig negativ 43 < 44 < 2-stellig 431 3-stellig positiv Lösung: −99 < −9 < 9 < 43 < 44 < 431 © Touchdown Mathe Seite 3 sponsored by GRUNDRECHENARTEN | Addition & Subtraktion: Rechenverfahren Bemerkung: Die Zeichen + und − sind mehrdeutig: sie können als Vorzeichen einer Zahl oder als Rechenzeichen zwischen zwei Zahlen auftreten. Das + als Vorzeichen kann man weglassen, z. B. 4 statt +4, aber das Rechenzeichen kann man nicht weglassen, z. B. ist 4 + 2 nicht dasselbe wie 42. Folgt ein Vorzeichen direkt auf ein Rechenzeichen, so muss die zweite Zahl (inklusive Vorzeichen) in Klammern gesetzt werden, z. B. 5 + (−2). Bemerkung: Die Grundrechenarten Addition und Subtraktion verhalten sich in Bezug auf die Ordnung ganzer Zahlen nach den folgenden Regeln: 1. Addiert man zu irgendeiner Zahl eine positive Zahl, so wird sie dadurch größer, denn Addition einer positiven Zahl entspricht einer Verschiebung nach rechts am Zahlenstrahl. Beispiele: ... ... 1 2 3 4 5 −4 −3 −2 −1 0 +2 +3 =⇒ 3 + 2 > 3, −1 + 3 > −1, usw. 2. Subtrahiert man von irgendeiner Zahl eine positive Zahl, so wird sie dadurch kleiner, denn Subtraktion einer positiven Zahl entspricht einer Verschiebung nach links am Zahlenstrahl. Beispiele: ... ... 1 2 3 4 5 −4 −3 −2 −1 0 −2 −3 =⇒ 3 − 2 < 3, −1 − 3 < −1, usw. © Touchdown Mathe Seite 4 sponsored by











