Probeklausur: Lösung Aufgabe 6

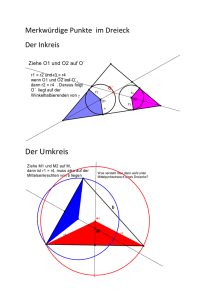
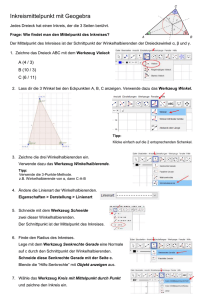
Probeklausur: Lösung Aufgabe 6
Hinweis: Fertigen Sie sich Skizzen für die Lösung an!
Aufgabe
Gegeben sei eine Ebene, in der alle Inzidenz-, Anordnungs- und Kongruenzaxiome gelten.
a) Formulieren Sie den Kongruenzsatz [SsW].
b) Sei ein Winkel ∠(h, k) gegeben. Beweisen Sie, dass ein Punkt im Inneren des Winkels genau
dann auf der Winkelhalbierenden dieses Winkels liegt, wenn die Lote auf die Schenkel gleich
lang sind.
c) Gegeben seien zwei nicht parallele Geraden, deren auf einem Blatt Papier sichtbaren Teile sich dort nicht schneiden. Leiten Sie eine Konstruktion mit einem Lineal, das nur eine
Zentimeter-Einteilung besitzt, der Winkelhalbierenden auf dem Papier her. Diskutieren Sie
die Korrektheit und Durchführbarkeit der Konstruktion.
Lösung: Zu (a) Zwei Dreiecke ∆(A, B, C) und ∆(A0 , B 0 , C 0 ) mit AB > AC sind kongruent, genau
dann, wenn AB ∼
= A0 B 0 , AC ∼
= A0 C 0 sowie ∠(ACB) ∼
= ∠(A0 C 0 B 0 ). (1 Punkt)
Zu (b) Sei P ein Punkt im Inneren des Winkels, O der Schenkel des Winkels und H ∈ h̄ bzw. K ∈ k̄
die Lotfußpunkte des Punktes P auf die Geraden h̄ und k̄, die die jeweiligen Strahlen enthalten.
(⇒) Liege P auf der Winkelhalbierenden. Angenommen einer der beiden Lotfußpunkte liegt außerhalb des Strahls, also z.B. H 6∈ h. Dann wäre ∠(OP, h) der Außenwinkel des Dreiecks ∆(O, H, P
und damit größer als der rechte Winkel ∠(P OH), also ein stumpfer Winkel. Halbe Winkel sind
aber immer spitz. Also liegen beide Fußpunkte auf den Strahlen. Dann gilt ∠(P OH) ∼
= ∠(P OK)
(P liegt auf Winkelhalbierender), P O = P O sowie ∠(P HO) ∼
= ∠(P KO) (rechte Winkel). Also
sind nach [WSW] die Dreiecke ∆(O, P, H) ∼
= ∆(O, P, K) kongruent und insbesondere P H ∼
= P K.
∼
(⇐) Seien die Lote P H = P K kongruent. Außerdem ist wider OP = OP und ∠(P HO) ∼
= ∠(P KO)
(rechte Winkel). Rechte Winkel sind immer die größten Winkel und da einem solchen die größte
Seite gegenüberliegt, können wir [SsW] anwenden, so das gilt: ∆(O, P, H) ∼
= ∆(O, P, K). Insbesondere isind die Winkel ∠(P OH) ∼
= ∠(P OK). Die Lote der Punkte im Inneren eines spitzen Winkels
auf dessen Schenkel liegen immer auf denselben. Der Punkt P liegt entweder auf der Winkelhalbierenden w (was zu zeigen ist) oder im Inneren von eines der beiden Winkel die diese mit h und
k formt. Angenomen, Sie liege im Inneren von ∠(h, w). Dann leigt H ∈ h auf dem Schenkel, da
halbe Winkel spitz sind. Ware K 6∈ k, dann läge H im Inneren von ∠(KOP im Widerspruch zur
Kongruenz. Also liegen H ∈ h und K ∈ k und somit P ∈ w auf der Winkelhalbierenden.
(4 Punkte: 2 Punkte für jede Richtung. Die fehlende Diskussion der Lage der Fußpunkte führt
zu einem Abzug von 0.5 Punkten. Die Nichterwähnung der Voraussetzung OP > OH führt zum
Abzug von einem Punkt.)
Zu (c) Wähle zwei Punkte A und B auf den gegebenen Geraden g und h . Konstruiere mit dem
Lineal die Winkelhalbierenden der folgenden Winkel: die g und G(A, B) in A auf der Seite, in der B
liegt, bzw. h und G(A, B) in B auf der Seite, in der A liegt, bilden (Beschreibung und Begründung
dieser Konstruktion später). Behauptung: Die Winkelhalbierenden die jeweils auf derselben Seite
von AB liegen schneiden sich in U bzw. V . Da U auf einer Winkelhalbierenden in A liegt, sind
die Lotstrecken von U auf g bzw. G(A, B) kongruent. Da U auch auf einer Winkelhalbierenden
in B liegt, sind die Lotstrecken von U auf h und G(A, B) kongruent. Also sind die Lotstrecken
von U auf g und h kongruent. Wegen der eingangs gemachten Auswahl der Seiten der Winkel,
die halbiert wurden, liegt U im Inneren des gegebenen Winkels. Aus (b) folgt, dass U auf der
Winkelhalbierenden liegt. das Gleiche gilt für V . U und V sind also zwei Punkte auf der gesuchten
Winkelhalbierenden und diese ist folglich durch die Gerade G(U, V ) bestimmt.
Durchführbarkeit der Konstruktion von U und V : Da die Strahlen Winkelhalbiernde sind, formen
sie mit AB jeweils spitze Winkel. Zwei Strahlen in A bzw. B auf derselben Seite von AB, die mit
AB spitze Winkel formen, schneiden sich: die zugehörigen Geraden müssen sich schneiden, da die
Gegenwinkel keine nebenwinkel voneinander sein können. Die ”Gegenstrahlen” bilden mit AB zwei
stumpfe Winkel und können sich daher nicht schneiden, da es in einem Dreieck höchstens einen
stumpfen Winkel geben kann. Also schneiden sich die Strahlen selbst.
Zur Konstruktion der Winkelhalbierenden in A bzw. B. Gegeben sei ein Winkel ∠(k, l) in O. Trage
Punkte C, D ∈ k und E, F in l ab, so dass OC ∼
= OE (z.B. 1cm) und OD ∼
= OF (z.B. 2cm). G sei
der Schnittpunkt von CF und DE. Behauptung: der Strahl in O durch G ist die gesuchte Winkelhalbierende. Durchführbarkeit und Korrektheit dieses Teils der Konstruktion: Der Schnittpunkt G
existiert wegen Pasch. OC ∼
= OE, OD ∼
= OF sowie ∠(COF ) ∼
= ∠(EOD) implizieren nach [SWS]
die Kongruenz der Dreiecke ∆(C, O, F ) ∼
= ∆(E, O, D) und insbesondere ∠(OF C) ∼
= ∠(ODE) und
∠(F CD) ∼
= ∠(DEF ) (letztere sind kongruente Außenwinkel). Weiterhin ist CD ∼
= EF (im Beispiel
2 − 1 = 1cm) und wegen [WSW] ∆(C, D, G) ∼
= ∆(E, F, G) und damit CG ∼
= EG. Da weiterhin
∼
OC = OE nach Konstruktion und OG = OG ist nach [SSS] ∆(O, C, G) ∼
= ∆(O, E, G),insbeondere
∠(COG) ∼
= ∠(EOG) w.z.b.w.
(5 Punkte: für die Idee, Winkelhalbierende der Winkel, die a bzw. b mit AB formen und die
Begründung 2 Punkte, für die Idee der Konstruktion dieser Winkelhalbierenden mit Begründung
2 Punkte, für die Begründung der Durchführbarkeit (Existenz der Schnittpunkte) 1 Punkt)