EdM Elemente der Mathematik Lineare Algebra/Analytische
Werbung
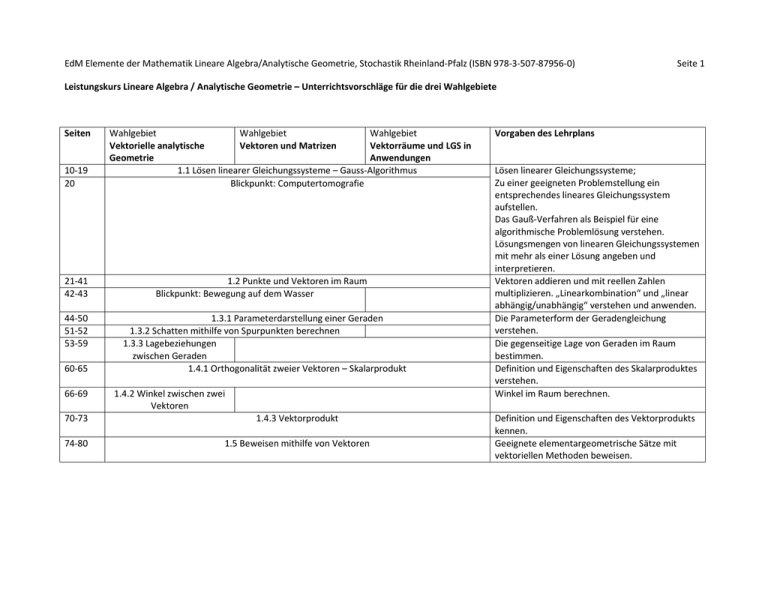
EdM Elemente der Mathematik Lineare Algebra/Analytische Geometrie, Stochastik Rheinland-Pfalz (ISBN 978-3-507-87956-0) Seite 1 Leistungskurs Lineare Algebra / Analytische Geometrie – Unterrichtsvorschläge für die drei Wahlgebiete Seiten 10-19 20 21-41 42-43 44-50 51-52 53-59 60-65 66-69 Wahlgebiet Wahlgebiet Wahlgebiet Vektorielle analytische Vektoren und Matrizen Vektorräume und LGS in Geometrie Anwendungen 1.1 Lösen linearer Gleichungssysteme – Gauss-Algorithmus Blickpunkt: Computertomografie 1.2 Punkte und Vektoren im Raum Blickpunkt: Bewegung auf dem Wasser 1.3.1 Parameterdarstellung einer Geraden 1.3.2 Schatten mithilfe von Spurpunkten berechnen 1.3.3 Lagebeziehungen zwischen Geraden 1.4.1 Orthogonalität zweier Vektoren – Skalarprodukt 1.4.2 Winkel zwischen zwei Vektoren 70-73 1.4.3 Vektorprodukt 74-80 1.5 Beweisen mithilfe von Vektoren Vorgaben des Lehrplans Lösen linearer Gleichungssysteme; Zu einer geeigneten Problemstellung ein entsprechendes lineares Gleichungssystem aufstellen. Das Gauß-Verfahren als Beispiel für eine algorithmische Problemlösung verstehen. Lösungsmengen von linearen Gleichungssystemen mit mehr als einer Lösung angeben und interpretieren. Vektoren addieren und mit reellen Zahlen multiplizieren. „Linearkombination“ und „linear abhängig/unabhängig“ verstehen und anwenden. Die Parameterform der Geradengleichung verstehen. Die gegenseitige Lage von Geraden im Raum bestimmen. Definition und Eigenschaften des Skalarproduktes verstehen. Winkel im Raum berechnen. Definition und Eigenschaften des Vektorprodukts kennen. Geeignete elementargeometrische Sätze mit vektoriellen Methoden beweisen. EdM Elemente der Mathematik Lineare Algebra/Analytische Geometrie, Stochastik Rheinland-Pfalz (ISBN 978-3-507-87956-0) Seite 2 Leistungskurs Lineare Algebra / Analytische Geometrie – Unterrichtsvorschläge für die drei Wahlgebiete Seiten Wahlgebiet Vektorielle analytische Geometrie Wahlgebiet Vektoren und Matrizen 81-89 94-99 100-106 110-115 116-120 Wahlgebiet Vektorräume und LGS in Anwendungen 1.6 Höherdimensionale Vektoren – Vektorräume 2.1.1 Parameterform einer Ebene 2.1.2 Lagebeziehungen zwischen Gerade und Ebene 2.1.3 Lagebeziehungen zwischen zwei Ebenen 2.2.1 Normalenform und Koordinatenform einer Ebene 2.2.2 Untersuchung von Lagebeziehungen mithilfe von Normalenvektoren Vorgaben des Lehrplans Die Menge der Pfeilklassen und die Menge der Zahlen n-Tupel als Beispiele für einen Vektorraum verstehen. Die allgemeine Definition der linearen Abhängigkeit/Unabhängigkeit am Beispiel des IRn erläutern. Die Begriffe „Erzeugendensystem“, „Basis“, „Dimension“ eines Vektorraums verstehen. Die Parameterform der Ebenengleichung verstehen. Die gegenseitige Lage von Geraden und Ebenen im Raum bestimmen und die Verfahren begründen. Die allgemeine Normalenform der Ebenengleichung herleiten. Die gegenseitige Lage von Geraden und Ebenen im Raum bestimmen und die Verfahren begründen. Die gegenseitige Lage gegebener Geraden und Ebenen durch Zeichnen in einem Koordinatensystem veranschaulichen. EdM Elemente der Mathematik Lineare Algebra/Analytische Geometrie, Stochastik Rheinland-Pfalz (ISBN 978-3-507-87956-0) Seite 3 Leistungskurs Lineare Algebra / Analytische Geometrie – Unterrichtsvorschläge für die drei Wahlgebiete Seiten 121-159 164-186 187-201 202-219 Wahlgebiet Vektorielle analytische Geometrie 2.3 Bestimmen von Abständen im Raum 2.4 Bestimmen von Winkeln im Raum 2.5 Kreis und Kugel Blickpunkt: GPS – Global Positioning System Wahlgebiet Vektoren und Matrizen Wahlgebiet Vektorräume und LGS in Anwendungen Vorgaben des Lehrplans Winkel und Abstände im Raum berechnen. Die allgemeine und die Hessesche Normalenform der Ebenengleichung herleiten und anwenden. 3.1 Matrizen – Addieren und Vervielfachen 3.2 Multiplikation von Matrizen 3.3 Materialverflechtung 3.4 Chiffrieren und Dechiffrieren – Inverse Matrix Blickpunkt: Input-Output-Analyse – Das Leontief-Modell 3.5 Beschreiben von Zustandsänderungen durch Matrizen 3.6 Abbildungsmatrizen Die Kreis- und Kugelgleichung herleiten und zur Untersuchung von Lagebeziehungen anwenden. Operationen mit Matrizen und Vektoren verstehen und im Zusammenhang mit nicht geometrischen Sachbezügen anwenden. In mindestens einem nicht geometrischen Anwendungsfeld von Matrizen Sachaufgaben lösen. Anwendungen: Zustandsvektoren und Übergangsmatrizen; Untersuchung auf Fixelemente Die allgemeine Matrix-Vektorgleichung einer affinen Abbildung verstehen. Eigenschaften der affinen Abbildungen beweisen. Kongruenz- und Ähnlichkeitsabbildungen als spezielle affine Abbildungen verstehen. Affine Abbildungen nach Fixelementen untersuchen. Eigenvektoren einer linearen Abbildung bestimmen und in Sachzusammenhängen deuten.