Mathe an Stationen

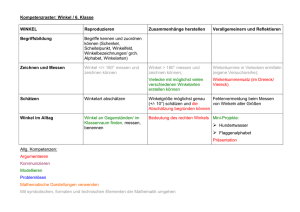
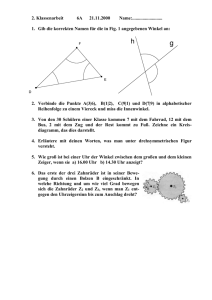
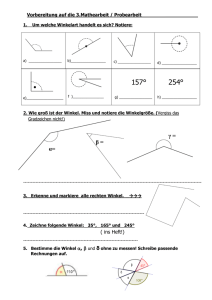
Sezer Avci
Mathe an Stationen
Spezial Winkel
Zusammenfassung der Winkel
I
arstufe
Sekund
vci
Sezer A
SPEZI
Downloadauszug
D
ownloadauszug
aus
Originaltitel:
a
us dem Originaltit
tel:
AL
e
h
t
a
M
n
e
n
o
i
t
a
t
an S
Winkel
Mathe an Stationen
Spezial Winkel
Zusammenfassung der Winkel
Dieser Download ist ein Auszug aus dem Originaltitel
Mathe an Stationen Spezial Winkel
Über diesen Link gelangen Sie zur entsprechenden Produktseite im Web.
http://www.auer-verlag.de/go/dl7242
Materialaufstellung und Hinweise
Zusammenfassung der Winkel
Die Stationen 1 bis 8 sind in entsprechender Anzahl zu vervielfältigen und den Schülerinnen und
Schülern bereitzulegen. Als Möglichkeit zur Selbstkontrolle können die Lösungsseiten zur Verfügung
gestellt werden.
Station 1: Gleichschenklige Dreiecke – ein Modell
Tafelzirkel, (Tafel-)Geodreieck und Scheren bereitstellen.
Station 2: Überstumpfe Winkel – Trifiguro
Schere, Kleber und ggf. leere Blätter bereitstellen.
Alternativen: Die Kärtchen auf dickes Papier kopiert, laminiert und ausgeschnitten
einer Dose oder
schnitten in ein
Schachtel bereithalten.
Station 3: Gleichseitige und gleichschenklige Dreiecke – Puzzles
Scheren bereitstellen.
Alternative: Die Kärtchen auf farbiges, dicke
dickes Papier
laminiert
pier kopiert, la
miniert und ausgeschnitten in einer
ner
Dose oder Schachtel bereithalten.
Station 4: Innenwinkelsumme von Dreiecken – Kartenspiel
artens iel
Scheren bereitstellen.
Alternative: Die Kärtchen a
auf
dickes Papie
Papier kopiert, laminiert und ausgeschnitten
einer
uf farbiges, dicke
schnitten in eine
Dose oder Schachtel bereithalten.
ereit alten.
Station 5: Innenwinkel von
Vierecken – Würfelspiel
on Dreiecken und
nd Vierecke
Spielpläne
Standard-Würfel (je 2 Würfel pro Gruppe) bereitstellen.
e und Standard-Wü
ellen.
Station 6: Vielecke im Koordinatensys
Koordinatensystem
Geodreiecke und farbige S
Stifte (Bunt- oder Filzstifte) bereitstellen.
Geodreieck
eitstellen.
Station 7: Mittelpunkt
Mittelpunktswinkel
Statio
nkel in Farbe
Stifte (Bunt- oder Filzstifte)
Farbige Stif
te) bereitstellen.
tellen.
Station
8: Wichtige
Wichtiges zu Winkeln – Rätsel
ion 8
sel
Lernzielkontrolle:
Zusammenfassung der Winkel
nzielk
1
Laufzettel
für
Pflichtstationen
Stationsnummer
erledigt
kontrolliert
t
erledigt
kontrolliert
Nummer
Nummer
Nummer
Nummer
Nummer
Nummer
Nummerr
Numme
Nummer
Nummer
Nu
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Nummer
Wahlstationen
ahlstati
Stationsnummer
Nummer
Nummer
Nummer
Nummer
2
Name:
Gleichschenklige Dreiecke –
ein Modell
Zusammenfassung
Station 1
Spielanleitung (3 – 4 Spieler)
In diesem Spiel ist der Tafelzirkel ein Modell für gleichschenklige Dreiecke.
Dabei steht der Zirkel für die gleichlangen Schenkel des Dreiecks und die Tischverbindung der Berührungspunkte für die Basis des Dreiecks.
Der Erste stellt mithilfe des Zirkels ein gleichschenkliges Dreieck seiner Wahl ein. Jeder
Mitspieler schätzt die Winkelgröße an der Spitze des gleichschenkligen
Dreiecks und nonD
tiert den Wert auf einem Blatt Papier. Wenn alle fertig sind, werden die
Werte aufgedeckt.
e We
Jetzt misst ein Spieler mit einem (Tafel-)Geodreieck die tatsächliche Größe
röße des gesuchten Winkels. Die geschätzten Werte werden mit dem gemessenen Wert vergl
verglichen. Wer
die beste Schätzung abgegeben hat, erhält einen Punkt. Der nächste
ste Spieler stellt
s
sein
Dreieck ein.
Es gewinnt der Spieler, der nach sechs Runden die meisten
sten Punkte hat.
Spielplan
Name des Spielers 1:
Runde
Schätzwert
S elplan
Spielplan
Name des Spielers 2:
Na
gemessener
messener Wert Punkte
Runde
1
1
2
2
3
3
4
4
5
5
6
6
Schätzwert
hätzw
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Summe:
gemessener
Punkte
gem
ssener Wert P
Summe:
Spielplan
elplan
Name des
s Spielers 3:
Runde
Schätzwert
Sch
Spielplan
Name des Spielers 4:
gemessener Wert Punkte
Runde
1
1
2
2
3
3
4
4
5
5
6
6
Summe:
Schätzwert
gemessener Wert Punkte
Summe:
3
Überstumpfe Winkel – Trifiguro
Aufgabe
Beim Zeichnen eines überstumpfen Winkels hilft es, den Winkel sinnvoll zu teilen: in einen gestreckten Winkel (180°) und in den verbleibenden Rest (spitzer, rechter oder stumpfer Winkel).
Beispiel: 320° = 180° + 140°.
Im unten stehenden Trifiguro gehören deshalb immer die Rechnung und das Ergebnis zusammen.
Schneide die Kärtchen aus. Beginne mit dem fett markierten Dreieck. Klebe den fertigen Stern auf
ein Blatt oder in dein Heft.
270°
2
0°
18
0°
+
334°
0
18
22
4°
°
53
1
°+
18
°
44
0°
+9
6°
180° + 105°
18
3°
0°
+
33
6°
8°
+1
8°
19
0
18
18
285°
27
0°
18
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
0°
12
+
°
3°
16
°
62
+
0°
0°
18
2°
0°
+7
6°
180° + 90°
30
34
3°
24
2
56
°
180° + 154°
180
180° + 125°
305°
50
4
Zusammenfassung
Name:
Station 2
Name:
Gleichseitige und gleichschenklige Dreiecke – Puzzles
Zusammenfassung
Station 3
Aufgabe
Schneidet zusammen die Puzzleteile aus.
Mischt die Puzzleteile und legt sie wieder richtig zusammen.
Puzzle 1: Winkel in gleichseitigen Dreiecken
Alle Innenwinkel eines
ne
gleichseitigen
ig n D
Dreiecks
reie
eck
sind
d glei
gleich
ich groß.
roß.
Jeder
60°.
J
ed beträgt
eträg
gt 60°
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Puzzle
uzzle 2:
2 Basiswinkel in gleichschenkligen
ch
gen Dreiecke
Dreiecken
Die zwei
B
Basiswinkel eines
gleichschenkligen
Dreiecks haben die
gleiche Winkelgröße.
5
51
Name:
Innenwinkelsumme von
Dreiecken – Kartenspiel (1)
Zusammenfassung
Station 4
Spielanleitung (2 – 3 Spieler)
Schneidet die Spielkarten aus. Mischt sie und bildet zwei verdeckte Stapel:
einen Stapel mit „Stern-Karten“ (Winkelgröße für a) und einen mit „Raute-Karten“
(Winkelgröße für b).
Jeder zieht zwei Karten (eine „Stern-Karte“ und eine „Raute-Karte“) und legt diese offen
vor sich hin.
mt durc
durch KopfrechWenn ein Dreieck mit diesen Werten für a und b möglich ist, bestimmt
diesen Werten
nen den fehlenden Winkelwert für g, doch sagt ihn noch nicht. Wenn mit dies
e neue Kar
Kartenpaare,
für a und b kein Dreieck möglich ist, zieht derjenige Spieler solange
bis ein Dreieck möglich ist. Mischt anschließend die Stapel neu.
er Spieler mit dem größ
größten WinNennt dann nacheinander den berechneten Winkel g. Der
ächste Run
Runde
de zieh
zieht jeder wieder
kel g bekommt die Karten der anderen Spieler. Für die nächste
zwei Karten.
Das Spiel endet, wenn die Kartenstapel
el auf
aufgebraucht
braucht sind
sind.. Gewi
Gewinner ist der Spielerr mit
den meisten Karten.
10°
10
1
a=
20°
20
a=
30°
30
a=
40°
a=
55°
a=
65°
a=
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
6
75°
a=
85°
a=
34°
a=
51°
51
a=
48°
48
a=
2
27°
a=
50°
50
b=
60°
b=
70°
b=
80°
b=
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Station 4
Innenwinkelsumme von
Dreiecken – Kartenspiel (2)
Zusammenfassung
Name:
7
53
15°
b=
25°
b=
35°
b=
45°
b=
54°
b=
41°
b=
26°
b=
38°
b=
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Station 4
Innenwinkelsumme von
Dreiecken – Kartenspiel (3)
Zusammenfassung
Name:
8
9
Innenwinkel
nkel von Dreiecken
ken und Vierecken – Würfelspiel
Name:
a
Winkelgröße b
Winkelgröße g
Dreieck ABC
Winkelgröße b
Winkelgröß
Winkelgröße
kelgröße g
Viereck A
ABCD
Winkelgröße d
Zusammenfassung
Punkte
Spieler 1 beginnt und würfelt mit beiden Würfeln auf einmal, so erhält
hält er den
nW
Wert für Winkel a (s. Beispiel). Alle notieren den Wert für a in
ihrem Spielplan. Jeder ergänzt nun in seinem Spielplan di
die Werte für die
ie restlichen
restlic
Winkel im Dreieck und Viereck. Die einzelnen Werte
sind frei wählbar, die Winkelsumme muss jedoch
edoch eingehalt
eingehalten werden.. Wenn alle ffertig sind, werden die Ergebnisse verglichen und die
Punkte vergeben.
nem Würfel.
W
zahl des Würfels gibt die Spalte an. Die Winkelgröße dieser SpalDie Punkte werden erwürfelt. Jeder würfelt mit einem
Die Augenzahl
te ist seine Punktzahl für diese Runde.
Beispiel: Man würfelt eine 1, damit schaut man in S
Spalte
palte 1 nac
nach: Spalte 1 = Winkel a = 64°; also erhält man 64 Punkte.
er Spieler, de
der am Ende der
er fü
fünf
nf Runde
Runden am meisten Punkte hat, hat gewonnen.
Nun bestimmt Spieler 2 den nächsten Winkel a. Der
Jeder Spieler benötigt einen Spielplan.
plan. A
Als
ls Gru
Gruppe benötigt ihrr zwei Wür
Würfel. Mit den Würfeln wird die Größe von Winkel a bestimmt:
Der Zahlenwert des links liegenden Würfels gibt den Zehnerwert
wert des Win
Winkels an und der rechts liegende Würfel den Einerwert.
Beispiel: Links liegt eine 6, rechts liegt
gt eine 4, so
somit ergibt sich:: a = 64°.
Spielanleitung (2 – 3 Spieler)
Station 5
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Name:
Station 6
Zusammenfassung
Vielecke im Koordinatensystem
Aufgabe
a) Benenne die drei Vielecke im Koordinatensystem.
b) Markiere und benenne die Eckpunkte der Vielecke. Notiere (unten) die Koordinaten dieser Eckpunkte.
c) Miss danach die Innenwinkel der Vielecke und notiere die Werte im Koordinatensystem.
en Bestimmt die
d) Alle drei Vielecke ergeben zusammen ein großes Vieleck (alle „Außenkanten“).
Innenwinkelsumme dieser Figur.
e) Vergleicht eure Ergebnisse und verbessert euch gegenseitig.
y
9
8
7
6
5
4
3
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
2
1
1
2
3
4
5
6
7
8
9
10
11
12
13
Vieleck 1 (dicke Linien)
Vieleck 2 (gestrichelte Linien)
Vieleck 3
Name:
Name:
Name:
Eckpunkte:
Eckpunkte:
Eckpunkte:
14
15
16 x
10
Name:
Station 7
Zusammenfassung
Mittelpunktswinkel in Farbe
Aufgabe
Berechne die Winkelgröße jeweils eines Mittelpunktwinkels in den nachfolgenden regelmäßigen
Vielecken und notiere diese. Male im unteren Bild die Felder mit den Lösungszahlen aus.
Mittelpunktswinkel:
In jedem regelmäßigen Vieleck gibt es einen Mittelpunkt M. Die Eckpunkte werden mit ihm verbunden.
Es entstehen gleichschenklige Dreiecke. Der Winkel
an der Spitze eines solchen Dreiecks ist ein Mittelpunktswinkel a. Alle zusammen ergeben 360°.
M
a
a is
ist ein
Mittel
Mittelpunktswinkel
Die Größe eines Mittelpunktswinkels in …
.
gt:
b) … einem regelmäßigen Achtzehneck beträgt:
.
c) … einem regelmäßigen Neuneck beträgt:
.
d) … einem regelmäßigen Fünfeck
ünfeck beträgt:
beträgt
.
e) … einem regelmäßigen
äßigen Zehneck b
beträgt:
ägt
.
f) … einem regelmäßigen
regelmäßigen Achteck beträgt:
.
g) … einem regelmäßigen
regelmäßig Zwanzigeck beträgt:
.
h) … einem regelmäßigen Fünfzehneck
ck beträgt:
.
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
a) … einem regelmäßigen Sechseck beträgt:
11
57
Name:
Station 8
Zusammenfassung
Wichtiges zu Winkeln – Rätsel
Aufgabe
Löse das Rätsel und trage jeweils den richtigen Lösungbuchstaben unten ein. So ergibt sich das
Lösungswort.
wahr (w) /
falsch (f)
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Aussage
14
Bei einem gleichschenkligen Dreieck heißen die gleich großen Winkel Ba
Basiswinkel.
w: A
f: E
9
Die Wechselwinkel an sich schneidenden Geraden ergänzen sich zu 180°.
w: T
f: S
12
Ein rechter Winkel hat die Größe: ein Drittel eines Vollwinkels.
nkels.
w: I
f: E
10
ünfec beträgt 108
Ein Innenwinkel eines regelmäßigen Fünfecks
108°.
w: S
f: F
3
äßigen Sec
secks sind
d nicht gleich groß.
Die Innenwinkel eines regelmäßigen
Sechsecks
w:: L
f N
f:
6
leichschen igen Drei
nwin
nk gleic
oß.
Es gilt: Bei jedem gleichschenkligen
Dreieck sind alle Innenwinkel
gleich groß.
w: B
f: L
11
hschenklig
ge Dreieicke kö
Gleichschenklige
können auch gleichseitig sein.
w: G
f: E
1
Rech
hte Winkel s
pitze Winkel.
kel.
Rechte
sind größer als spitze
w: W
f: S
7
Ein Vollwinkel ist doppelt so groß
oß wie ein ges
treck Winkel.
gestreckter
w: M
f: G
16
inke und der äußere verbleibende Winkel erBei Vielecken gilt:: Je ein Innenwinkel
60°.
gänzen sich zu 3
360°.
w: T
f: W
4
ad ist
st die Einheit der Winkelgröße.
W
Grad
w: K
f: B
13
n regelm
mäßig 10-Eck hat die Innenwinkelsumme von 1 000°.
Ein
regelmäßiges
w: N
f: R
2
„a, b, g, d“ bedeuten nacheinander im Deutschen: „Delta, Alpha, Gamma,
Beta“.
w: E
f: I
15
Wenn g ein überstumpfer Winkel ist, so gilt: 180° < g < 360°.
w: E
f: R
5
Scheitelwinkel ergänzen sich nie zu einem gestreckten Winkel.
w: A
f: E
8
Ein Winkel besteht aus zwei Schenkeln.
w: E
f: A
Lösungswort:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12
Name:
Zusammenfassung der
Winkel (1)
Aufgabe 1
Teile den gegebenen überstumpfen Winkel in jeweils einen gestreckten und den verbleibenden Winkel auf. Notiere die Summe.
a) 310° =
b) 275° =
c) 256° =
d) 302° =
e) 195° =
f) 211° =
Aufgabe 2
Ergänze die Lücken der folgenden
nden S
Sätze.
ätze.
(1)
LLE WI
(2) DI
S
B
KE
SISWI
ND GL
IIC
IN EIN
KEL EINE
M G
G
EICH
EICH
EI
IGEN D
CHE
EIEC
EC
KLIGEN D
SIN
EIE
LEICH GR
KS
ROß.
Aufgabe
ufg
3
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Die folgenden Aussagen
sage sind falsch. Korrigiere
orri
sie.
a) Es gilt: Bei
Bei jedem gleichschenkligen
gleichsche
Dreieck sind alle Innenwinkel gleich groß.
richtig:
htig:
b) Ein regelmäßiges 10-Eck hat die Innenwinkelsumme von 1 000°.
richtig:
c) Ein spitzer Winkel ist größer als ein rechter Winkel.
richtig:
13
ß.
Zusammenfassung
Lernzielkontrolle
Name:
Zusammenfassung der
Winkel (2)
Zusammenfassung
Lernzielkontrolle
Aufgabe 4
Berechne die Größe der fehlenden Innenwinkel.
Dreieck ABC
a
Winkelgröße b
62°
101°
54°
84°
Viereck ABCD
Winkelgröße g
Winkelgröße b
59°
47°
62°
132°
Winkelgröße g
Winkelgröße d
34°
98°
129°
55°
Aufgabe 5
Gib für die verschiedenen Vielecke
e jeweils
eweils die Größe
Gr ße eines
ei
Mittelpunktswinkels an.
Die Größe eines Mittelpunktswinkels
ktswinkels in
n…
.
b) … einem
eine regelmäßigen
regelmäßig Ze
Zehneck beträgt:
.
c) … einem regelmäßigen
regelmä
Achteck beträgt:
eträgt:
.
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
a) … einem regelmäßigen
gelmäßigen Fünfeck beträgt:
be
14
18
4°
22
3°
96
°
15
°+
18
0
44
°
+
0°
3°
33
27
6°
0°
+
°
18
18
°
+
0°
18
8
19
180° + 154°
+
0°
18
76
°
°
62
18
0°
+
+
0°
18
16
3°
0°
12
18
0°
+
0°
30
34
3°
2°
24
334°
180° + 105°
25
6°
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Lösungen:
Zusammenfassung
Station 2: Überstumpfe Winkel – Trifiguro
Seite 270°
285°
28
180°
0° + 125
125°
15
180° + 90°
305
305°
Seite 5
Lösungen:
Zusammenfassung
Station 3: Gleichseitige und gleichschenklige Dreiecke – Puzzles
Alle Innenwinkel eines
gleichseitigen Dreiecks
sind gleich groß.
Jeder beträgt
be ägt 60°.
Die zw
zwei
Basis
ne
es
Basiswinkel ei
eines
hsc henk
klig
gleichschenkligen
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Dre
cks h
Dreiecks
haben die
gle
eic
gleiche
Winkelgröße.
16
Lösungen:
Zusammenfassung
Seite Station 6: Vielecke im Koordinatensystem
a) – c)
y
V4
9
87°
8
D1
F4
53°
64°
7
6
23°
F5
5
166°
104°
4
3
2
D3
86°
D2
V3
41°
V1
F1
146°
43°
121°
V2
F3
1
146°
1
2
3
4
5
6
7
8
9
10 F2 1
11
1
12
2
13
1
14
15
16 x
Vieleck 1 (dicke Linien)
Vieleck 2 (gest
(gestrichelte
ichelte L
Linien)
Vieleck
leck 3
Name: Dreieck
Eckpunkte:
D1 (3|8)
D2 (5|4)
D3 (14|6))
Name: Vie
Viereck
eck
Eckpunkte:
V1 (0
(0|3)
V2 (8|2)
V3 (12|4)
V4 (9|9)
Name:
me
e: Fünfeck
Eckpu kte:
Eckpunkte:
F1 (1|2)
F2 (10|0)
F3 (15|2)
F4 (16|8)
F5 (6|5)
elsumme von
v 1 800°.
800
d) Das Zwölfeck hat eine Innenwinkelsumme
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Station 7: Mittelpunktswinkel
elpunkts
in F
Farbe
a)
h)
Seite a = 60
60°;
0°; b) a = 20°
20°; c) a = 40°; d) a = 72°; e) a = 36°; f) a = 45°; g) a = 18°;
a = 24
24°
17
wahr (w) /
falsch (f)
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag
g – AAP Lehrerfachverlage
g GmbH,, Donauwörth
Aussage
14
Bei einem gleichschenkligen Dreieck heißen die gleich großen Winkel Basiswinkel.
w: A
9
Die Wechselwinkel an sich schneidenden Geraden ergänzen sich zu 180°.
f: S
12
Ein rechter Winkel hat die Größe: ein Drittel eines Vollwinkels.
f: E
10
Ein Innenwinkel eines regelmäßigen Fünfecks beträgt 108°.
w: S
3
Die Innenwinkel eines regelmäßigen Sechsecks sind nicht gleich groß.
ß.
f: N
6
nwinkel gleich
gle
eich groß.
Es gilt: Bei jedem gleichschenkligen Dreieck sind alle Innenwinkel
f: L
11
Gleichschenklige Dreieicke können auch
uch g
gleichseitig
seitig sein.
w: G
1
Rechte Winkel sind größer als spitze Winkel.
nkel.
w: W
7
Ein Vollwinkel ist doppelt so groß wie ein g
gestreckter
strec
Winkel.
w: M
16
Bei Vielecken gilt:
Innenwinkel
t: Je ein Inne
winkel und der äußere verbleibende
bend
de Winkel
Winke ergänzen sich
h zu 360°.
w: T
4
Grad
Einheit
ad ist die E
inheit der Winkelgröße.
Win
w: K
13
Ein
10-Eck hat die Innenwinkelsumme
E
in regelmäßiges
regelmäß
In
nkelsumme von
vo 1 000°.
f: R
2
„a, b, g, d“ bedeuten nacheinander
ander im Deutschen:
Deu schen: „Delta, Alpha, Gamma, Beta“.
f: I
15
Wenn g ein überstumpfer
stump Winkel
el ist, so gil
gilt: 180° < g < 360°.
w: E
5
Scheitelwinkel
inkel ergänzen
rgänz sich nie zu einem gestreckten Winkel.
f: E
8
Ein Winkel besteht aus zwei Schenkeln.
w: E
Lösungswort:
Lösungen:
Zusammenfassung
Seite Station 8: Wichtiges zu Winkeln – Rätsel
W
I
N
K
E
L
M
E
S
S
G
E
R
A
E
T
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
18
Seite Lösungen:
Zusammenfassung
Lernzielkontrolle: Zusammenfassung der Winkel
1) a) 310° = 180° + 130°
b) 275° = 180° + 95°
c) 256° = 180° + 76°
d) 302° = 180° + 122°
e) 195° = 180° + 15°
f) 211° = 180° + 31°
2) a) ALLE WINKEL IN EINEM GLEICHSEITIGEN DREIECK SIND GLEICH GROß.
LEICH GROß.
b) DIE BASISWINKEL EINES GLEICHSCHENKLIGEN DREIECKS SIND GLEICH
nkel gleich
g ich groß.
3) a) Es gilt: Bei jedem gleichschenkligen Dreieck sind die Basiswinkel
b) Ein regelmäßiges 10-Eck hat die Innenwinkelsumme von 1 440°.
echter Winkel.
kel.
c) Ein spitzer Winkel ist kleiner als ein rechter
4)
Dreieck ABC
BC
Viereck ABCD
CD
a
Winkelgröße
ß b
Winkelgröße
Winkelg
ße g
Winkelgröße b
Winkelgröße
nk
kelg ße g
Winkelgröße d
Winkelg
62°
101°
101
17°
17
166°
34°
98°
67°
54°
59°
47°
1
117°
129°
84°
34°
62°°
132°
55°
89°
5) a) 72°
Sezer Avci: Mathe an Stationen Spezial: Winkel
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
b) 36°
c) 45°
19
Impressum
© 2015
Verlag
5 Auer Ver
g
AAP Lehrerfachverlage
ehrerfachv age GmbH
Gmb
Alle Rechte vorbehalten.
vorbehal
Das Werk als Ga
Ganzes sowie in seinen Teilen unterliegt dem deutschen Urheberrecht. Der Erwerber
des Werkes ist berechtigt, das Werk als Ganzes oder in seinen Teilen für den eigenen Gebrauch
und den Einsatz im Unterricht zu nutzen. Die Nutzung ist nur für den genannten Zweck gestattet,
nicht jedoch für einen weiteren kommerziellen Gebrauch, für die Weiterleitung an Dritte oder für
die Veröffentlichung im Internet oder in Intranets. Eine über den genannten Zweck hinausgehende
Nutzung bedarf in jedem Fall der vorherigen schriftlichen Zustimmung des Verlages.
Die AAP Lehrerfachverlage GmbH kann für die Inhalte externer Sites, die sie mittels eines Links
oder sonstiger Hinweise erreichen, keine Verantwortung übernehmen. Ferner haftet die AAP
Lehrerfachverlage GmbH nicht für direkte oder indirekte Schäden (inkl. entgangener Gewinne), die
auf Informationen zurückgeführt werden können, die auf diesen externen Websites stehen.
Autor: Sezer Avci
Illustrationen: Carmen Hochmann, Steffen Jähde, Stefan Leuchtenberg, Corina Beurenmeister
www.auer-verlag.de