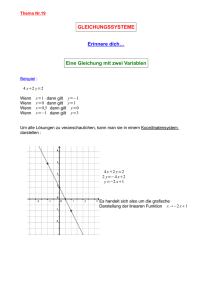
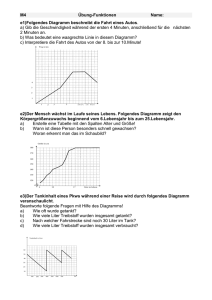
Aufgaben zur Wiederholung
Werbung

Ungleichungen und Gleichungen
Aufgaben zur Wiederholung
Arbeitsblatt
1
lgebraisches Lösen linearer Ungleichungen
A
Löse die Gleichung über ℝ, gib die Lösungsmenge an und stelle sie grafisch dar.
a) (3 x − 5)×8 < 15 + 2×(5 x − 3)
b) 70 − 21 x < 10 − 3×(2 x + 5)
c) 2×(6 x − 1) ≥ 12 x + 27
d) 3×(x + 4) ≤ 6 + 5×(x − 2)
e) (x + 2)(x − 3) > (x − 4)(x + 1)
f) (x − 4)2 ≤ (x + 3)(x − 3)
2
ngleichungsketten
U
Für welche reellen Zahlen x gilt die Ungleichungskette? Löse durch Aufspalten in zwei Ungleichungen. Gib die Lösungsmenge an und stelle sie grafisch dar.
a) 12 − x ≤ 3 x < 12 + x
b) 3 − 5 x ≤ 3 + 9 x ≤ 15 + x
c) 4 − 3 x < x − 2 < 4 + 3 x
x − 2
x
x
d) 2×(x + 1) < 25 − x < 7 x + 3
e) _
< 6 − _
< 3×(2 x + 1)
f) 5 − 3 x ≤ _
− 2 ≤ 0
3
3
3
ngleichungen mit Fallunterscheidungen
U
Löse die Ungleichung in ℝ, stelle die Lösungsmenge grafisch dar und führe eine geeignete Überprüfung durch.
3
x + 4
a) _
< 1
2 x − 7
b) _
≥ 3
3 x + 9
3
c) _
< − _
d) |3 x + 8| < 5
e) |5 − 4 x| ≤ 2
f) | − 2 x − 5| > 3
5 − x
2 x + 5
g)x2 − 4 x − 21 > 0
h)
7 − 2 x
x2 − 14 x + 49 ≤ 0
2
i) (x − 5)(x + 6) ≥ 0
Wurzelgleichungen
⊳
Beispiel:
_____
__
_____
Löse für die Grundmenge G = ℝ die Gleichung √
x + 1 +
√ 2 – x =
√ 6 .
Lösung:
In dieser Gleichung
treten _____
mehrere __
Wurzeln auf.
_____
√x + 1 +
√ 2 – x =
√ 6 |2
_____
_____
) = 6
( √x + 1 +
√ 2 – x
2
Die linke Seite wird nach (a + b)2 = a2 + 2 a b + b2 aufgelöst.
_____
_____
(x + 1) + 2×√x + 1
×√
2 – x + (2 – x) = 6
_____
_____
√x + 1
2×
×√
2 – x + 3 = 6
| – 3
Durch Äquivalenzumformungen wird die Wurzel auf einer Seite der Gleichung isoliert.
____________
2×
) = 3
√(x + 1)×(2 – x
|÷2
____________
(x + 1)×(2 – x
) = 1,5
√
| 2
(x + 1)×(2 – x) = 2,25
– x2 + x + 2 = 2,25
| + x2 – x – 2
0 = x2 – x + 0,25
x1 = x2 = 0,5
___
____
__
√ 1,5 =
√ 6
Probe: √
1,5 +
___
___
_____
√1,5 +
√ 1,5 =
√ 4×1,5
___
___
2×
√1,5 = 2×
√1,5
wahre Aussage
_____
_____
__
Die Lösungsmenge der Gleichung √
x + 1 +
√ 2 – x =
√ 6 ist L = {0,5}.
© 2015 Verlag E. DORNER, Wien
Dimensionen – Mathematik 6
1
Ungleichungen und Gleichungen
4
urzelgleichungen
W
Löse______
die Gleichung
für G = ℝ und überprüfe
______
______ die__Lösung.
_____
______
_____
√x + 7 ___
√______
a)
2 x + 5 +
√ 2 x – 3 = 4
b)√______
4 x + 9 –
√_____
x =
√ x + 5
c)√______
x + 14 = 7 –
______
d)√2 x – 3 + 4 = 0
e)√2 x + 5 –
√ x – 6 = 3
f)√2 x – 2 +
√ 2 x + 8 =
√ 20
Löse______
die folgenden
Aufgaben
mithilfe eines elektronischen Tools.
______
______
√2 x + 4 =
√
g)√_____
2 x – 3 +
_____
8 x + 1
______
_____
√x + 1 +
h)
√ x + 2 =
√ x + 34 –
√ x + 7
y (in km)
i)Ein Hubschrauber, der im Punkt (0 | 0) stationiert ist, hat die
Aufgabe, verletzte Personen von der Autobahn (Gerade y = 20)
40
in das Krankenhaus, das im Punkt (80 | – 40) liegt, zu bringen.
Autobahn V
Der Pilot setzt den Verletzten im Krankenhaus ab und notiert
20
20 x (in km)
im Logbuch 140 geflogene Kilometer. An welcher Stelle x der
H
x
Autobahn hat der Pilot den Verletzten aufgenommen?
20 40 60 80
– 20 O
j)
Zwei Orte A und B haben von einer geradlinig
verlaufen–
20
___
40
den Eisenbahnstrecke die Abstände
AC = a = 5 km
und
___
___
– 40
KH
BD = b = 7 km.
Die Gleislänge CD
= c beträgt 12 km. An der
80 x
Strecke CD befindet sich ein Bahnhof. Die Strecke von A zum
Bahnhof und anschließend zu B beträgt 17,5 km. Wie weit ist der Bahnhof von C entfernt? Für
diese Aufgabe gibt es zwei Lösungen.
5
äherungsverfahren zum Lösen von Gleichungen
N
Löse die Gleichung grafisch und mithilfe der Regula falsi auf 2 Dezimalstellen genau.
a)0,1x3 − 0,3x2 + 0,5 x − 0,7 = 0
b) − 32x3 − 4,2x2 − 0,06 x + 1,33 = 0
c) − 2x3 + 5,6x2 − 4,44 x − 5,68 = 0
© 2015 Verlag E. DORNER, Wien
Dimensionen – Mathematik 6
2