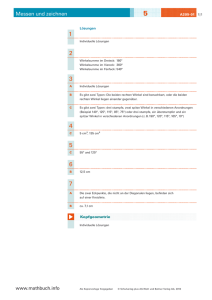
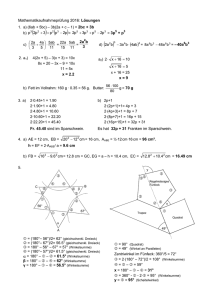
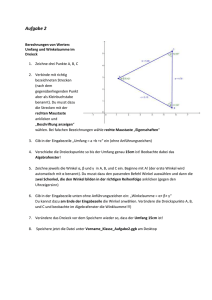
216a) (1) Winkelsumme im Dreieck: 180° Winkelsumme im Viereck

216a)
(1)
Winkelsumme im Dreieck: 180°
Winkelsumme im Viereck: 360°
Ein regelmäßiges Sechseck besteht aus sechs gleichseitigen Dreiecken mit der Winkelsumme 180°(je drei
Winkel zu 60°). Da aber nur die Winkel am Rand und nicht die in der Mitte gezählt werden muss man 6 ∙ 60°
= 360° abziehen.
Die Winkelsumme eines regelmäßigen Sechsecks ist also 6 ∙ 180° - 360° = 1080° - 360° = 720°
(2)
Ein regelmäßiges Fünfeck besteht aus fünf gleichschenkeligen Dreiecken mit der Winkelsumme 180°. Da die
Winkel innen wieder nicht mitgezählt werden, zieht man 360° ab. Diesen Wert erhält man, wenn man sich
vorstellt, dass alle Winkel in der Mitte zusammen einen ganzen Kreis ergeben.
Die Winkelsumme eines regelmäßigen Fünfecks ist daher 5 ∙ 360 - 360 = 540°
© Österreichischer Bundesverlag Schulbuch GmbH & Co. KG, Wien 2015. | www.oebv.at | Lösungswege 5 SB | ISBN: 978-3-209-08466-8
Alle Rechte vorbehalten. Von dieser Druckvorlage ist die Vervielfältigung für den eigenen Unterrichtsgebrauch gestattet.
Die Kopiergebühren sind abgegolten. Für Veränderungen durch Dritte übernimmt der Verlag keine Verantwortung.