Mathematik 3. Klasse

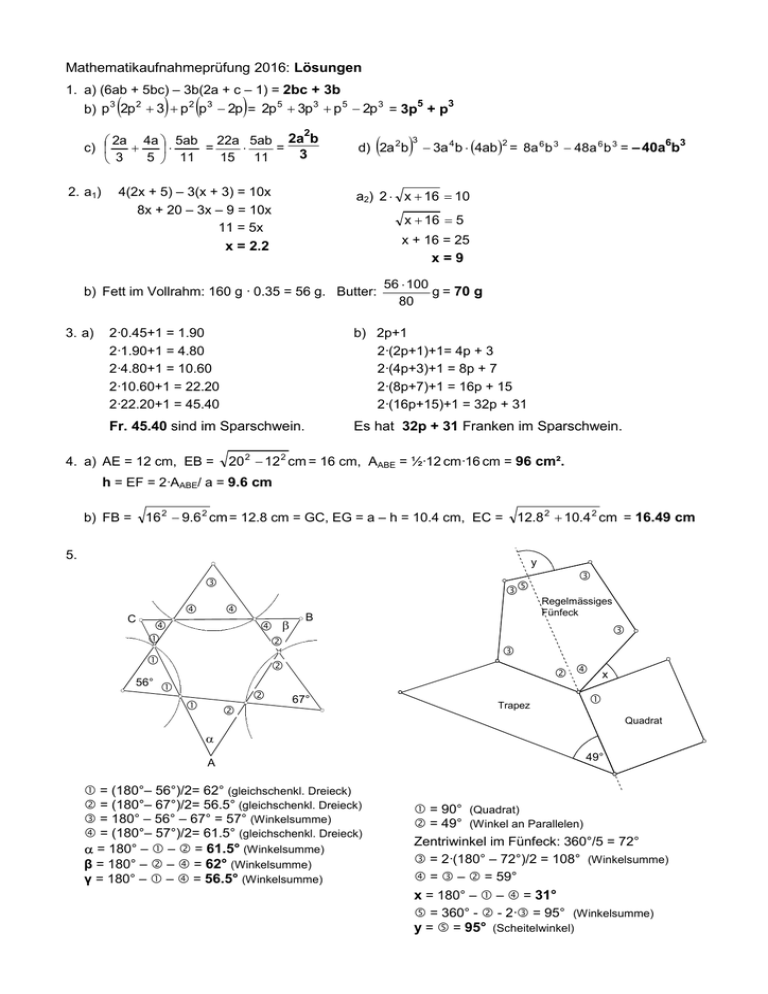
Mathematikaufnahmeprüfung 2016: Lösungen
1. a) (6ab + 5bc) – 3b(2a + c – 1) = 2bc + 3b
(
)
(
)
5
3
b) p 3 2p 2 + 3 + p 2 p 3 − 2p = 2p 5 + 3p 3 + p 5 − 2p 3 = 3p + p
(
2
 2a 4a  5ab 22a 5ab 2a b
c) 
=
=
+
⋅
⋅
3
5  11
15 11
 3
2. a1)
4(2x + 5) – 3(x + 3) = 10x
8x + 20 – 3x – 9 = 10x
11 = 5x
x = 2.2
d) 2a 2 b
3
− 3a 4 b ⋅ (4ab ) = 8a 6 b 3 − 48a 6 b 3 = – 40a b
6 3
2
a2) 2 ⋅ x + 16 = 10
x + 16 = 5
x + 16 = 25
x=9
b) Fett im Vollrahm: 160 g · 0.35 = 56 g. Butter:
3. a)
)
56 ⋅ 100
g = 70 g
80
2·0.45+1 = 1.90
2·1.90+1 = 4.80
2·4.80+1 = 10.60
2·10.60+1 = 22.20
2·22.20+1 = 45.40
b) 2p+1
2·(2p+1)+1= 4p + 3
2·(4p+3)+1 = 8p + 7
2·(8p+7)+1 = 16p + 15
2·(16p+15)+1 = 32p + 31
Fr. 45.40 sind im Sparschwein.
Es hat 32p + 31 Franken im Sparschwein.
4. a) AE = 12 cm, EB =
20 2 − 12 2 cm = 16 cm, AABE = ½·12 cm·16 cm = 96 cm².
h = EF = 2·AABE/ a = 9.6 cm
16 2 − 9.6 2 cm = 12.8 cm = GC, EG = a – h = 10.4 cm, EC =
b) FB =
12.8 2 + 10.4 2 cm = 16.49 cm
5.
y
C
β
Regelmässiges
Fünfeck
B
x
56°
67°
Trapez
Quadrat
α
A
= (180°– 56°)/2= 62° (gleichschenkl. Dreieck)
= (180°– 67°)/2= 56.5° (gleichschenkl. Dreieck)
= 180° – 56° – 67° = 57° (Winkelsumme)
= (180°– 57°)/2= 61.5° (gleichschenkl. Dreieck)
α = 180° – – = 61.5° (Winkelsumme)
β = 180° – – = 62° (Winkelsumme)
γ = 180° – – = 56.5° (Winkelsumme)
49°
= 90° (Quadrat)
= 49° (Winkel an Parallelen)
Zentriwinkel im Fünfeck: 360°/5 = 72°
= 2·(180° – 72°)/2 = 108° (Winkelsumme)
= – = 59°
x = 180° – – = 31°
= 360° - - 2· = 95° (Winkelsumme)
y = = 95° (Scheitelwinkel)
6.
p
8
a) - Winkelhalbierende w
- Parallele p zu BC im Abstand 3
- w mit p schneiden → B‘
- Mittelsenkrechte von B und B‘→
Spiegelachse a
- Dreieck ABC an a spiegeln
a
C
7
w
6
5
1
C'
B' 4
b) A’: dx = 12 – (-63) = 75
x = 12 + 75 = 87
3
A
dy = 3 – 25 = -22
2
1
y = 3 – 22 = -19
A’(87/-19)
B
0
–6
–5
–4
–3
–2
–1
0
1
2
3
4
5
6
7
8
B’: dx = 12 – 5 = 7
–1
x = 12 + 7 = 19
–2
dy = 3 – (-35) = 38
y = 3 + 38 = 41
–3
B’(19/41)
–4
A'
a 2 + a 2 = 122 + 122 cm = 288 cm = 12 ⋅ 2 cm = 16.971 cm
7. a) CG =
BM =
a 2 + ( a2 ) 2 = 122 + 6 2 cm =
BF =
BM2 + a 2 =
180 + 12 2 cm =
180 cm = 13.416 cm
324 cm = 18 cm
u = 12 cm + 16.971 cm + 6 cm + 18 cm = 52.971 cm ≈ 52.97 cm
3
a + a2
a
3 2
3
⋅a = 2 ⋅a = a·a = a
b) A =
4
4
2
2
8. a)
30000
21000
20100
20010
20001
12000
10200
10020
10002
11100
11010
11001
10110
10101
10011
Es gibt 15 fünfstellige Zahlen mit der
Quersumme 3.
b) 300000000000
210000000000
120000000000
111000000000
101100000000
100110000000
100011000000
100001100000
usw.
100000000110
100000000011
1
11
11
10
9
8
7
6
…
2
1
1+11+11+10+9+8+7+6+5+4+3+2+1 = 78
Es gibt 78 zwölfstellige Zahlen mit der Quersumme 3.