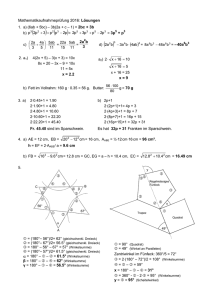
Wie groß ist die Winkelsumme im Dreieck?

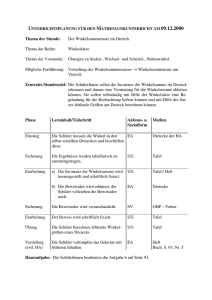
Schule: HS USH
Buch: Lernstufen Mathematik 7
Fach:
Lehrplan: 7.4.1 Geometrische Flächen
Mathe
Lehrer: RS
Klasse:
7
Thema: Wie groß ist die Winkelsumme im Dreieck?
Lernziele: Die S sollen:
- die Winkel verschiedener Dreiecke messen und nennen können.
- erkennen, dass die Winkelsumme im Dreieck immer 180° beträgt.
- Vermutungen zur Winkelsumme im Viereck anstellen.
Phasen
Einstieg:
Erarbeitung:
Unterrichtsinhalte
Sozialf.
L zeigt Bilder von verschiedenen Dreiecken
S beschriften diese und nennen ihre Eigenschaften
(gleichschenkliges, rechtwinkliges, stumpfes, …)
Kopfgeometrie,
Bild, SA
L: „Zeichnet ein beliebiges Dreieck; schneidet es aus und
messt alle drei Winkel.“
L zu S: „Nenne mir α und β und ich nenne dir γ!“
LV
L-S-Gespräch
 Wie groß ist die Winkelsumme im Dreieck?
L tippt an die Überschrift -> S vermuten
Impuls, SÄ
AA:
-
Arbeitsauftrag,
EA
-
Zeichne drei beliebige Dreiecke in dein Heft und
beschrifte diese.
Miss die Innenwinkel in den Dreiecken A, B und C.
Addiere die Größen der Innenwinkel.
Notiere, was dir auffällt.
S äußern sich und präsentieren ihre Ergebnisse.
SÄ
S stellen die Vermutung an: „Die Winkelsumme im Dreieck SÄ
ist immer gleich groß. Die Winkelsumme beträgt 180°.“
Schluss:
S bekommen AB „Winkelsumme im Dreieck“ und
bearbeiten dies.
AB, EA
S erarbeiten mit dem L das Tafelbild
L-S-G
S übernehmen das Tafelbild in ihr Heft.
SA
S berechnen Aufgaben bzgl. der Winkelsumme im Dreieck
im Buch.
Buch
Ausblick/Transfer: L zeichnet ein Quadrat an die Tafel und
schreibt 𝜶 + 𝜷 + 𝜸 + 𝜹 = __ °
S äußern sich.
Transfer, LA
SÄ
Geplantes Tafelbild:
Wie groß ist die Winkelsumme im
Dreieck?
<Schülervermutungen>
-
Beschrifte die Dreiecke A, B und C.
Miß die Innenwinkel in den Dreiecken A, B und C.
Addiere die Größen der Innenwinkel.
C
B
A
Dreieck
A
B
C
α
β
γ
α+ β+γ
 Die Winkelsumme im Dreieck ist immer gleich groß.
 Die Winkelsumme im Dreieck beträgt immer 180°.
 𝜶 + 𝜷 + 𝜸 = 𝟏𝟖𝟎 °