α γ δ ε - Robert-Koch

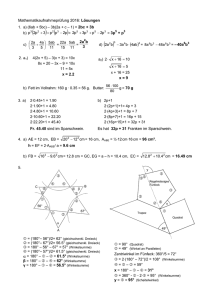
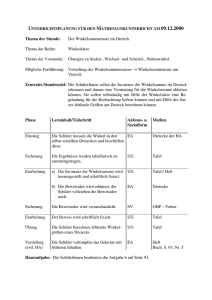
Klasse 7 A
2. Schulaufgabe aus der Mathematik
Gruppe
14. 01. 2000
A
1. Gleichungen. Gib die Lösungsmenge für x ∈ Q an.
a) 17 − 1, 8 · [5x − 2 · (3 − x)] = 21, 5
2
1
b) 12 − 4, 5 · 4 − 2x = 8 − 1, 4x
3
3
2. Geburtstagsrätsel
An ihrem Geburtstag, sagt die jetzt 40-jährige Mutter zu ihrer Tochter, die an diesem
Tag auch Geburtstag feiern kann: ,,Als ich so alt war, wie du jetzt bist, da dauerte
es noch 14 Jahre bis Du geboren wurdest.“
Wie alt ist die Tochter?
Löse die Aufgabe mit Hilfe einer Gleichung.
(Eventuell eine Hilfe: Schema: Heute – Zeitpunkt der Geburt der Tochter)
3. Winkelberechnungen
γ
Gegeben ist die nebenstehende Figur.
Dabei ist
α = 63, 42◦ und
γ = 56◦ 10 1200 .
a) Übertrage die gegebene Zeichnung in Originalgröße auf dein
Blatt.
b) Rechne γ um in Dezimaldarstellung.
ε
δ
α
c) Berechne den Winkel δ aus den gegebenen Winkeln. (Trage dazu Bezeichnungen
in die Zeichnung von Teilaufgabe a ein.)
d) Berechne den Winkel ε aus den gegebenen Winkeln.
4. Im Pentagon
Ein Fünfeck mit fünf gleich langen Seiten und
fünf gleich großen Innenwinkeln heißt regelmäßiges
Fünfeck.
α
a) Wie viele Symmetrieachsen weist ein solches
Fünfeck auf?
b) Bestimme den Innenwinkel α eines regelmäßigen
Fünfecks.
Viel Erfolg !
Kink
Klasse 7 A
2. Schulaufgabe aus der Mathematik
Gruppe
14. 01. 2000
B
1. Gleichungen. Gib die Lösungsmenge für x ∈ Q an.
a) 13 − 2, 2 · [5x − 3 · (2 − x)] = 17, 4
1
1
b) 13 − 4, 5 · 5 − 2x = 6 − 1, 4x
3
3
2. Geburtstagsrätsel
An seinem Geburtstag, sagt der jetzt 45-jährige Vater zu seinem Sohn, der an diesem
Tag auch Geburtstag feiern kann: ,,Als ich so alt war, wie du jetzt bist, da dauerte
es noch 19 Jahre bis Du geboren wurdest.“
Wie alt ist der Sohn?
Löse die Aufgabe mit Hilfe einer Gleichung.
(Eventuell eine Hilfe: Schema: Heute – Zeitpunkt der Geburt des Sohnes)
3. Winkelberechnungen
Gegeben ist die nebenstehende Figur.
Dabei ist
α = 56◦ 10 1200 und
β = 63, 42◦ .
ε
a) Übertrage die gegebene Zeichnung in Originalgröße auf dein
Blatt.
δ
α
β
b) Rechne α um in Dezimaldarstellung.
c) Berechne den Winkel δ aus den gegebenen Winkeln. (Trage dazu Bezeichnungen
in die Zeichnung von Teilaufgabe a ein.)
d) Berechne den Winkel ε aus den gegebenen Winkeln.
4. Im Pentagon
Ein Fünfeck mit fünf gleich langen Seiten und
fünf gleich großen Innenwinkeln heißt regelmäßiges
Fünfeck.
α
a) Wie viele Symmetrieachsen weist ein solches
Fünfeck auf?
b) Bestimme den Innenwinkel α eines regelmäßigen
Fünfecks.
Viel Erfolg !
Kink
Klasse 7 A
2. Schulaufgabe aus der Mathematik
Gruppe
A
– Musterlösung 1 –
1. a)
17 − 1, 8 · [5x − 2 · (3 − x)] = 21, 5,
17 − 1, 8 · [5x − 6 + 2x] = 21, 5,
17 − 1, 8 · [7x − 6] = 21, 5,
17 − 12, 6x + 10, 8 = 21, 5,
−12, 6x = 21, 5 − 17 − 10, 8,
−12, 6x = −6, 3,
63
1
1
x=
= , L=
.
126
2
2
b)
2
1
12 − 4, 5 · 4 − 2x = 8 − 1, 4x,
3
3
9
14
1
12 − ·
− 2x = 8 − 1, 4x,
2
3
3
126
1 7
12 −
+ 9x = 8 − x,
6
3 5
7
1
9x + x = 8 − 12 + 21,
5
3
52
1
x = 17 ,
5
3
52
52
x= ,
5
3
52 5
5
2
2
x=
·
= =1 , L= 1
.
3 52
3
3
3
2. Alter in Jahren:
Jetzt :
Mutter : 40
Tochter : x
Vor x Jahren :
Mutter : 40 − x = x + 14
(Tochter : 0)
x + 14 = 40 − x
2x = 26
x = 13
Die Tochter ist jetzt 13 Jahre alt.
14. 01. 2000
Klasse 7 A
2. Schulaufgabe aus der Mathematik
Gruppe
14. 01. 2000
A
– Musterlösung 2 –
3. a)
γ
h
g
γ'
ε
δ
α
β
12◦
5◦
1◦
6◦
2◦
1◦
= 56◦ +
+
= 56◦ +
= 56◦ +
=
b) γ = 56◦ 10 1200 = 56◦ + +
60 3600
300 300
300
100
◦
56, 02
c) β = 180◦ − (α + γ) = 180◦ − (63, 42◦ + 56, 02◦ ) = 180◦ − 119, 44◦ = 60, 56◦
(Winkelsumme im Dreieck).
δ = 360◦ − 2 · 90◦ − β = 180◦ − 60, 56◦ = 119, 44◦
d) γ = γ
0
(Winkelsumme im Viereck).
(Stufenwinkel an g q h).
◦
ε = 180 − 90◦ − γ 0 = 90◦ − 56, 02◦ = 33, 98◦
(Winkelsumme im Dreieck).
4. a) Das Pentagon weist 5 Symmetrieachsen auf.
360◦
b) ε =
= 72◦
5
α
2·
= 180◦ − 72◦ = 108◦ (Winkelsumme im
2
Dreieck).
α = 108◦
α
ε
Klasse 7 A
2. Schulaufgabe aus der Mathematik
Gruppe
B
– Musterlösung 1 –
1. a)
13 − 2, 2 · [5x − 3 · (2 − x)] = 17, 4,
13 − 2, 2 · [5x − 6 + 3x] = 17, 4,
13 − 2, 2 · [8x − 6] = 17, 4,
13 − 17, 6x + 13, 2 = 17, 4,
−17, 6x = 17, 4 − 13 − 13, 2,
−17, 6x = −8, 8,
88
1
1
x=
= , L=
.
176
2
2
b)
1
1
13 − 4, 5 · 5 − 2x = 6 − 1, 4x,
3
3
9
16
1
13 − ·
− 2x = 6 − 1, 4x,
2
3
3
144
1 7
13 −
+ 9x = 6 − x,
6
3 5
7
1
9x + x = 6 − 13 + 24,
5
3
52
1
x = 17 ,
5
3
52
52
x= ,
5
3
52 5
5
2
2
x=
·
= =1 , L= 1
.
3 52
3
3
3
2. Alter in Jahren:
Jetzt :
Vater : 45
Sohn : x
Vor x Jahren :
Vater : 45 − x = x + 19
(Sohn : 0)
x + 19 = 45 − x
2x = 26
x = 13
Der Sohn ist jetzt 13 Jahre alt.
14. 01. 2000
Klasse 7 A
2. Schulaufgabe aus der Mathematik
Gruppe
14. 01. 2000
B
– Musterlösung 2 –
3. a)
γ
h
α'
δ
ε
α
β
g
12◦
5◦
1◦
6◦
2◦
1◦
◦
◦
◦
= 56 +
+
= 56 +
= 56 +
=
b) α = 56 1 12 = 56 + +
60 3600
300 300
300
100
◦
56, 02
◦
0
00
◦
c) γ = 180◦ − (α + β) = 180◦ − (56, 02◦ + 63, 42◦ ) = 180◦ − 119, 44◦ = 60, 56◦
(Winkelsumme im Dreieck).
δ = 360◦ − 2 · 90◦ − γ = 180◦ − 60, 56◦ = 119, 44◦
d) α = α0
(Stufenwinkel an g q h).
ε = 180◦ − 90◦ − α0 = 90◦ − 56, 02◦ = 33, 98◦
(Winkelsumme im Dreieck).
4. a) Das Pentagon weist 5 Symmetrieachsen auf.
360◦
b) ε =
= 72◦
5
α
2·
= 180◦ − 72◦ = 108◦ (Winkelsumme im
2
Dreieck).
α = 108◦
(Winkelsumme im Viereck).
α
ε