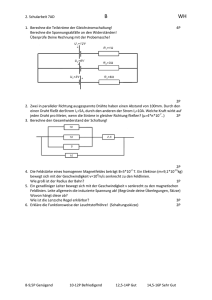
( 1 )( + − = nn nT hca A ⋅+ = ) (2

Grundwissensaufgaben Algebra – Jahrgangsstufe 7
Termberechnung:
n2 −1
1. Berechne die Werte der nebenstehenden Terme T1(n) = n + 2n + 1 und T2 (n) =
( n + 1) 2
2
jeweils für n = 1; 2; –3; –1,5; 1 ; 3
2
4
2
2. Berechne die Werte der nebenstehenden
Terme jeweils für a= -2; b = 1,5
1. T(a,b) = a – ab + 2,5b
2. T(a,b) = 3a – a(1 - 2b)
Lösen von Gleichungen
9. Bestimme die Lösungsmenge:
a) 4x + 3 = 2x + 9
b) 17x – 33 + 12x – 16 = 4x + 56 + 10x
c) 10 – 3(5 – 4x) = 15x + 40
10. Man erhält das Sechsfache einer Zahl, wenn man das Doppelte dieser Zahl um 12 vergrößert. Wie groß
ist die Zahl?
11. Ein Kaufmann mischt 50 kg Kaffee der Sorte A (Kilopreis: 8 €) mit 150 kg einer Sorte B
(Kilopreis: 12 €). Wie teuer wird ein kg der Mischung?
Terme aufstellen:
3.Die monatlichen Telefongebühren berechnen sich beim Konkurrenten von FONO
aus der Grundgebühr und der Anzahl der Nah- und Ferngespräche, wobei 8 Nahgespräche frei sind:
Grundgebühr: 13,60€; ein Nahgespräch kostet: 0,05€, ein Ferngespräch kostet:0,15€
Stelle einen Term für die Berechnung der monatlichen Telefongebühren auf wenn mehr als 8
Nahgespräche stattfinden.
4. Schau dir die folgende Reihe aus regelmäßig
wachsenden Plättchenmustern genau an und versuche,
sie fortzusetzen.
A, Wie viele Plättchen sind in der 1,2,3,4,...., n Figur
B, Wie viele Plättchen sind in der Grundseite, wenn
die gesamte Figur aus 68Plättchen besteht?
12. Gegeben ist ein gleichschenkliges Dreieck. Ein Basiswinkel ist um 300 größer als der Winkel an der
Spitze. Berechne die Winkel in dem Dreieck.
Prozentrechnung
13. In einem Unternehmen sind 80 Mitarbeiter beschäftigt. Davon arbeiten
in der Produktion
45%
im Außendienst
15%
in der Verwaltung
30%
in der Konstruktion
10%
a) Wie viele Personen sind in den einzelnen Bereichen des Unternehmens tätig?
b) Zeichne ein Kreisdiagramm.
14. Beim Kauf einer Wohnzimmereinrichtung werden 30% angezahlt. Dies sind 3852 €. Wie hoch ist der
Kaufpreis?
5. Für ein Festessen sollen Einzeltische für je sechs
Personen zu einer großen Tafel zusammengestellt
werden
Wie viele Personen können bei jeder
Tischanordnung insgesamt Platz nehmen,
wenn 1,2,3,4,...., n Tische aufgestellt werden?
15. Ein Schulzentrum wird von 315 Jungen und 435 Mädchen besucht. Wie viele Prozent sind Jungen, wie
viele Prozent sind Mädchen?
16. Nach einer Preiserhöhung von 6% kostet eine Ware 143,10 €. Berechne den alten Preis und die
Preiserhöhung in €!
Terme interpretieren.
6. Die beiden parallelen Seiten eines Trapezes werden mit a und c bezeichnet, die
Höhe mit h; für seinen Flächeninhalt gilt: A = 12 (a + c) ⋅ h
Wie ändert sich der Flächeninhalt des Trapezes, wenn
A, die Seite a um eine Längeneinheit verlängert und die Seite c um eine Längeneinheit verkürzt wird?
B, die Seite a und die Seite c verdoppelt werden?
C, die Seiten a und c und die Höhe h verdoppelt werden?
Termumformungen:
7. Fasse zusammen:
a) 14mn – 4m² + 5mn – 18mn + 5m²
b) 7ab – ba – 4a²b² – 3ab + 5b²a²
e) 5(2a – b) + (a + 3b) . 4
f) 18a² – 4a(3a – 2) + 15a²
c) 7a – (3b + 4c) + (2a – 5b)
g) (3y – 5)(7y – 11) – (2y – 1)(3y – 4)
d) 14x – (13 – 17x) + (–21y + 11x – 7)
8. Zerlege soweit wie möglich in Faktoren:
a) 5a4 – 6a3 + a2
b) –6a2 + 12ab + 8ac
h) 17xy – (4x + 3y)(8x – 2y)
c)
3x2y-5x3 y
17. Nach einer Preissenkung von 7,5% kostet eine Ware 203,50 €. Berechne den alten Preis und die
Preissenkung!
18. Ein Preis in Höhe von 250 € wird um 8% gesenkt, der neue Preis jedoch wegen steigender Kosten
wenig später um 10% erhöht. Berechne den endgültigen Preis
19. Der Preis einer Gefriertruhe wurde um 10% erhöht. Als daraufhin der Umsatz stark zurückging, wird
der erhöhte Preis wieder um 6% gesenkt. Wie hoch war der ursprüngliche Preis, wenn die Gefriertruhe
nach der Preissenkung 517 € kostet?