Mathplan 8.8.1 - educa.Unterricht

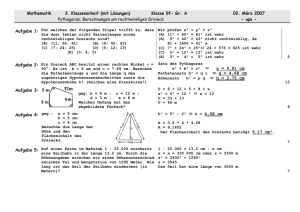
Mathplan 8.8.1
Geometrie
Dreiecke
Satz von Pythagoras
Hilfsmittel :
Zeitvorschlag:
Geometrie 2
2 Wochen
von:
am:
Lernkontrolle
Name:
A
b
s
c
b
M
bis
Probe 8.8.1
B
a
C
Wichtige Punkte:
Ich mache eine saubere, klare Konstruktionszeichnung und markiere das
Resultat (rot)
1. Selbständigkeit:
Ich wähle meinen Arbeitsort und meinen Arbeitspartner möglichst sinnvoll aus.
2. Hilfen:
erst wenn ich mich bemüht habe und trotzdem nicht klar komme, hole
ich mir Hilfe (mit dem bereits Gezeichneten als Grundlage)
3. Arbeitstempo:
rech-
Ich darf in meinem Tempo arbeiten (nicht trödeln).Die Zeit ist knapp benet. Für Sekundarschüler : Auswahl A (mindestens diefett gedruckten Nummern)
4. Hausaufgaben:
pro Woche 30 Minuten
Weiterarbeit am Arbeitsplan > grün umranden Zeit und das Datum dazu
setzen !
5. Selbstbeurteilung:
mit selbständig gelösten Tests (in die Liste FORMATIVE BEURTEILUNG eintragen! )
6. Auswertung:
Am Schluss des Planes Probe und Selbstbeurteilung auf der Rückseite
dieses Planes.
7. Übersicht
LP 95
Themenfeld
8.7.2
Arithmetik/Algebra Formeln
8.8.1
Geometrie
Dreiecke
Satz von Pythagoras
8.8.2
8.9
Geometrie
Satz von Pythagoras
Vierecke
Geometrie
Prisma
Zylinder
Anzahl
Wochen
Hilfsmittel
2
Algebra 2
Kapitel 3 + 4
2
2
2
Geometrie 2
Kapitel 4+5
Geometrie 2
Kapitel 6
Sachrechnen 2
Kapitel 2
Geometrie 2
Kapitel 3
Sachrechnen 2
Inhalte, Begriffe, Hilfsmittel
Auswahl A
Auswahl B
Dreiecke
G2: 401, 402, T17, 403
Kongruenzbedingungen (und
entsprechende Konstruktionen)
Winkelhalbierende, Inkreis;
Mittelsenkrechte, Umkreis;
Seitenhalbierende, Schwerpunkt
G2: 415, 416, 417, 418,
419, 420, 421, 422,
440, 441, 442, T19abe
Test 8.8.1
Fach 1
G2:
404, 405, 406, 407,
408, 409,410, 411,
T18, 412. 413, 414
G2:
427, 428, 430, 443,
444
Bearbeitet am:
Mittellinie, Höhengerade
G2:
423, 424. 425, 426,
429; 436,
437, 438,
439. T19 cd
Zusammenfassung (vermischte
Aufgaben)
G2: 445abcdefnop, 446cde
Test 8.8.2
S.78 Nr 452, 453,
G2:
445ghiklrnqrstuv,
446abf, 447, 448,
449, 450
Kontroll- und Knobelaufgaben
455 G2: 456, 457, 458, 459,
G2:
451, 454,
460 461
462 463
Satz von Pythagoras
Satz: a2 + b2 = c2; Kathete, Hypotenuse
G2: 502, T20, T21, 503,
504
Einfache Anwendungen bei geo-
G2: 506, 509, 510, 511,
Probe 8.8.1
Selbstbeurteilung:
Genaue Konstruktionen sind meine Stärke
Ich kann in der Geometrie den andern gut erklären
Weitere Bemerkungen zu diesem Mathplan:
Der Lehrer:
Die Eltern:
G2:
505
G2: 507, 508, 514, 515,
metrischen Berechnungen
516
stimmt
512, 513
stimmt nicht
Geometrie : Dreiecke 1
Geometrie : Dreiecke 1
Bezeichnung:
Bezeichnung:
C
Ecken :
Winkel :
b
Seiten :
a
Höhen :
c
B
b
Höhen :
C
s
sa
s
sb
S
c
A
B
sc
S
c
A
A
Winkelhalbierende: wα, wβ, wγ
C
sb
kleine Buchstaben
(a, b, c)
ha , hb, hc
c
B
sa
Grossbuchstaben
(A,B,C)
griechische Buchstaben α, β, γ
Seitenhalbierende: sa, sb, sc
A
C
s
Seiten :
a
Winkelhalbierende: wα, wβ, wγ
C
s
Ecken :
Winkel :
kleine Buchstaben
(a, b, c)
ha , hb, hc
Seitenhalbierende: sa, sb, sc
A
C
Grossbuchstaben
(A,B,C)
griechische Buchstaben α, β, γ
B
sc
gleichschenkliges Dreieck
gleiche Basiswinkel α = β
gleichseitiges Dreieck
drei Symmetrieachsen
2 gleichlange Schenkel (s)
eine Symmetrieachse >sc
3 gleichlange Seiten
Schnittpunkt ist der Schwerpunkt S
sa, sb, sc
B
sc
A
B
sc
gleichschenkliges Dreieck
gleiche Basiswinkel α = β
gleichseitiges Dreieck
drei Symmetrieachsen
2 gleichlange Schenkel (s)
eine Symmetrieachse >sc
3 gleichlange Seiten
Schnittpunkt ist der Schwerpunkt S
sa, sb, sc
Geometrie : Dreiecke 2
Geometrie : Dreiecke 2
A
A
Die Winkelhalbierenden der Innenwinkel schneiden sich im Mittelpunkt
(I) des Inkreises.
wα
Die Berührungsradien stehen senkrecht auf den Dreiecksseiten
wβ
B
Die Winkelhalbierenden der Innenwinkel schneiden sich im Mittelpunkt
(I) des Inkreises.
wα
Die Berührungsradien stehen senkrecht auf den Dreiecksseiten
wβ
B
C
C
C
C
Die Mittelsenkrechten der Dreieck-seiten schneiden sich im Mittelpunkt (U)
des Umkreises
mb
ma
Die Mittelsenkrechten der Dreieckseiten schneiden sich im Mittelpunkt
(U) des Umkreises
mb
ma
U
U
A
A
B
B
mc
mc
C
pc
A
c
Die Mittellinien verbinden je zwei Mittelpunkte von Dreiecksseiten. Sie sind
parallel zur dritten Seite und halb so
lang wie diese. c = 2·pc
C
Die Mittellinien verbinden je zwei Mittelpunkte von Dreiecksseiten. Sie sind
parallel zur dritten Seite und halb so
lang wie diese. c = 2·pc
pc
B
A
c
B
C
C
Die Höhengeraden schneiden sich im
Höhenschnittpunkt (H)
Die Höhengeraden schneiden sich im
Höhenschnittpunkt (H)
H
ha
H
A
A
B
A
B
Die Seitenhalbierenden (= Schwerelinien) verbinden die Seitenmitten mit
den gegenüberliegenden Ecken.
C
S
ha
sa
B
Sie schneiden sich im Schwerpunkt
(S). Dieser teilt die Seitenhalbierenden
im Verhältnis 1:2 , wobei der längere
Abschnitt von der Ecke bis zum
Schwerpunkt reicht.
Die Seitenhalbierenden (= Schwerelinien) verbinden die Seitenmitten mit
den gegenüberliegenden Ecken.
C
S
A
sa
B
Sie schneiden sich im Schwerpunkt
(S). Dieser teilt die Seitenhalbierenden im Verhältnis 1:2 , wobei der längere Abschnitt von der Ecke bis zum
Schwerpunkt reicht.
THEORIE : Pythagoras
THEORIE : Pythagoras
BEZEICHNUNGEN :
BEZEICHNUNGEN :
Im rechtwinkligen Dreieck nennt man die
beiden Seiten, die den rechten Winkel einschliessen, Katheten (a und b)
Die längste Seite liegt dem rechten Winkel
gegenüber und heisst Hypotenuse c
c
b
a
b2
C
a2
A
B
c2
h2
HÖHENSATZ :
Im rechtwinkligen Dreieck hat das Quadrat
über der Höhe den gleichen Flächeninhaltwie das Rechteck, gebildet aus beidenHypotenusenabschnitten.
h
p
q
p
PYTHAGORAS :
Der Satz des Pythagoras besagt:
Das Hypotenusenquadrat ist gleich gross
wie die beiden Kathetenquadrate zusammen:
c2 = a2 + b2
Dieser Satz ermöglicht, im rechtwinkligen
Dreieck aus zwei Seitenlängen die dritte zu
berechnen.
(Pythagoras war ein griechischer Mathematiker und Philosoph, der um 570 bis 480 vor
Chr. lebte.)
c
b
a
b2
C
a2
A
B
c2
h2
h
p
q
p
a
p
q
c
Im rechtwinkligen Dreieck hat das Quadrat
über einer Kathete den gleichen Flächeninhalt wie das Rechteck, gebildet aus der Hypotenuse und dem anliegenden
Hypotenusenabschnitt :
a2 = c · q
b2 = c · p
Dieser Satz ermöglicht, im rechtwinkligen
Dreieck aus zwei Seitenlängen die dritte zu
berechnen.
(Pythagoras war ein griechischer Mathematiker und Philosoph, der um 570 bis 480 vor
Chr. lebte.)
h2 = p · q
KATHETENSATZ :
KATHETENSATZ :
h
PYTHAGORAS :
Der Satz des Pythagoras besagt:
Das Hypotenusenquadrat ist gleich gross
wie die beiden Kathetenquadrate zusammen:
c2 = a2 + b2
HÖHENSATZ :
Im rechtwinkligen Dreieck hat das Quadrat
über der Höhe den gleichen Flächeninhaltwie das Rechteck, gebildet aus beidenHypotenusenabschnitten.
h2 = p · q
b
Im rechtwinkligen Dreieck nennt man die
beiden Seiten, die den rechten Winkel einschliessen, Katheten (a und b)
Die längste Seite liegt dem rechten Winkel
gegenüber und heisst Hypotenuse c
b
a
h
p
q
c
Im rechtwinkligen Dreieck hat das Quadrat
über einer Kathete den gleichen Flächeninhalt wie das Rechteck, gebildet aus der Hypotenuse und dem anliegenden
Hypotenusenabschnitt :
a2 = c · q
b2 = c · p
Name:
TEST
8.8.1
Dreiecke
Datum:
Konstruiere Dreiecke mit den nachstehenden Angaben: (Masse in cm)
mache zuerst eine Faustzkizze und trage das gegebene mit rotem Farbstift ein !
gib immer alle Lösungen an !
1.
2.
Geg:
b = 3,5
c = 2,5
ru = 2,0
Ges:
a
Geg:
a = 6,0
ha = 6,0
Ges:
3.
Geg:
Ges:
ß
b
=?
= 60°
=?
a = 7,0
sb = 5,4
sc = 6,6
c =?
Name:
TEST
8.8.1
Dreiecke
Datum:
Konstruiere Dreiecke mit den nachstehenden Angaben: (Masse in cm)
mache zuerst eine Faustzkizze und trage das gegebene mit rotem Farbstift ein !
gib immer alle Lösungen an !
1.
2.
Geg:
Ges:
a
Geg:
a = 6,0
ha = 6,0
Ges:
3.
b = 3,5
c = 2,5
ru = 2,0
Geg:
ß
b
=?
= 60°
=?
a = 7,0
sb = 5,4
sc = 6,6
Ges:
c
=?
Resultate:
1. Zwei Lösungen
a1 = 4,0 cm
a2 = 1,5 cm
2. b = 6,5 cm
3. c
= 6,2 cm
8.8.1 DREIECKSKONSTRUKTIONEN
Reihe A
alle Masse in cm
Resultat:
1,5 Pt
Faustskizze: 0,5 Pt
Genauigkeit -0,5 Pt
1.
a = 3,1
b = 3,5
c
= 4,3
Gesucht:
a
2.
c = 4,1
a = 5,4
b
= 120
Gesucht:
b = ? cm
3.
b = 3,8
a = 35
g
= 125
Gesucht:
a = ? cm
4.
b = 4,7
c
g
= 40
Gesucht:
a = ? cm
5.
b = 7,0
sb = 4,8
sc = 5,1
Gesucht:
c = ? cm
6.
b = 4,0
c
a = 125
Gesucht:
Umkreisradius r=?cm
und a = ? cm
7.
c = 6,0
a = 72
Umkreisrad. = 3,5
Gesucht:
a = ? cm
= 4,2
= 5,0
8.8.1 DREIECKSKONSTRUKTIONEN
Reihe B
alle Masse in cm
Resultat:
1,5 Pt
Faustskizze: 0,5 Pt
Genauigkeit -0,5 Pt
1.
a = 3,2
b = 5,8
c
= 3,4
Gesucht:
b
2.
b = 5,2
c
a = 54
Gesucht:
a = ? cm
3.
a = 7,0
b = 36
g
= 22
Gesucht:
b = ? cm
4.
b = 3,5
c
b
= 30
Gesucht:
a = ? cm
5.
a = 6,0
sb = 6.6
sc = 3,6
Gesucht:
b = ? cm
6.
b = 5,0
a = 100
c
Gesucht:
Umkreisradius r=?cm
und a = ? cm
7.
b = 3,8
g
Umkreisrad.= 3,0
Gesucht:
c = ? cm
= 4,6
= 6,4
= 110
= 5,0
8.8.1 DREIECKSKONSTRUKTIONEN
Reihe A
alle Masse in cm
LÖSUNGEN
Resultat:
1,5 Pt
Faustskizze: 0,5 Pt
Genauigkeit -0,5 Pt
1.
a = 3,1
b = 3,5
c
= 4,3
a = 45
2.
c = 4,1
a = 5,4
b
= 120
b = 8,25 cm
3.
b = 3,8
a = 35
g
= 125
a = 6,4 cm
4.
b = 4,7
c
g
= 40
a1 = 6,5 cm a2 = 0,7 cm
5.
b = 7,0
sb = 4,8
sc = 5,1
c = 6,7 cm
6.
b = 4,0
c
a = 125
Umkreisradius r=4,9cm
und a = 8,0 cm
7.
c = 6,0
a = 72
Ukreisrad = 3,5
a = 6,7 cm
= 4,2
= 5,0
8.8.1 DREIECKSKONSTRUKTIONEN
Reihe B
alle Masse in cm
Resultat:
1,5 Pt
Faustskizze: 0,5 Pt
Genauigkeit -0,5 Pt
b= 123
1.
a = 3,2
b = 5,8
c
2.
b = 5,2
c
a = 54
a = 4,5 cm
3.
a = 7,0
b = 36
g
= 22
b = 4,8 cm
4.
b = 3,5
c
b
= 30
a1 = 7,0 cm a2 = 4,1
5.
a = 6,0
sb = 6.6
sc = 3,6
b = 4,5 cm
6.
b = 5,0
a = 100
c
Umkreisradius r=3,9cm
und a = 7,6 cm
7.
b = 3,8
g
Ukreisrad = 3,0
= 4,6
= 6,4
= 110
= 3,4
LÖSUNGEN
= 5,0
c = 5,6 cm
Datum:
Pt
16
15.5
15
14.5
14
13.5
13
12.5
12
11.5
11
10.5
10
9.5
9
8.5
8
7.5
7
6.5
6
5.5
5
4.5
4
3.5
3
Datum:
A
B
Note
6
5.5
5
4.5
4
3.5
3
2.5
Pt
16
15.5
15
14.5
14
13.5
13
12.5
12
11.5
11
10.5
10
9.5
9
8.5
8
7.5
7
6.5
6
5.5
5
4.5
4
3.5
3
Datum:
A
B
Note
6
5.5
5
4.5
4
3.5
3
2.5
Pt
16
15.5
15
14.5
14
13.5
13
12.5
12
11.5
11
10.5
10
9.5
9
8.5
8
7.5
7
6.5
6
5.5
5
4.5
4
3.5
3
A
B
Note
6
5.5
5
4.5
4
3.5
3
2.5
Mathplan 8.8.2
Geometrie
Name:
Vierecke
Pythagoras
b2
C
a2
Hilfsmittel :
Zeitvorschlag:
Geometrie 2
2 Wochen
von:
am:
Lernkontrolle
A
B
bis
c2
Probe 8.8.2
Wichtige Punkte:
Ich mache eine saubere, klare Darstellung, schreibe die Aufgabenstellung ab und unterstreiche das Resultat doppelt.
1. Selbständigkeit:
Ich wähle meinen Arbeitsort und meinen Arbeitspartner möglichst sinnvoll aus.
2. Hilfen:
erst wenn ich mich bemüht habe und trotzdem nicht klar komme, hole
ich mir Hilfe (mit dem bereits Berechneten als Grundlage)
3. Arbeitstempo:
rech-
Ich darf in meinem Tempo arbeiten (nicht trödeln).Die Zeit ist knapp benet. Für Sekundarschüler : Auswahl A (mindestens diefett gedruckten Nummern) Für Spez.Sekundarschüler: nebst fettgedruckten Nr. auch noch Auf
gaben aus der Auswahl B. (speziell die Unterstrichenen)
4. Hausaufgaben:
pro Woche 30 Minuten
Weiterarbeit am Arbeitsplan > grün umranden Zeit und das Datum dazu
setzen !
5. Selbstbeurteilung:
mit selbständig gelösten Tests (in die Liste FORMATIVE BEURTEILUNG eintragen! )
6. Auswertung:
Am Schluss des Planes Probe und Selbstbeurteilung auf der Rückseite
dieses Planes.
7. Übersicht
LP 95
Themenfeld
8.7.2
Arithmetik/Algebra Formeln
8.8.1
Geometrie
Dreiecke
Satz von Pythagoras
8.8.2
8.9
Geometrie
Satz von Pythagoras
Vierecke
Geometrie
Prisma
Zylinder
Anzahl
Wochen
Hilfsmittel
2
Algebra 2
Kapitel 3 + 4
3
2
2
Geometrie 2
Kapitel 4+5
Geometrie 2
Kapitel 6
Sachrechnen 2
Kapitel 2
Geometrie 2
Kapitel 3
Sachrechnen 2
Inhalte, Begriffe, Hilfsmittel
Auswahl A
Vierecke
Typen: Quadrat, Rechteck,
Rhombus, Parallelogramm,
Trapez, symmetrischer Drachen
Eigenschaften, elementare Konstruktionen
G2: T22
Begriffe bei Konstruktionen
und Berechnungen anwenden
Auswahl B
Flächeninhalt, Umfang von Quadrat, Rechteck, Rhombus, Parallelogramm
G2:
S2:
602, 603
243, 250, 251
G2: 601
S2: 249, 252
AB8: 29
Flächeninhalt, Umfang von Trapez und Drachen
G2:
S2:
604, 605, 607, 608,
244, 245, 246, 247,
253
G2: 606, 610, 611
S2: 248, 254
Test 8.8.3 (Fach 3)
Andere Vielecke: Zerlegung in
bekannte Figuren, Flächeninhalt
G2: 612, 613, 614
S2:
255
AB8: 30
G2: 615, 616
S2: 256, 257
AB8: 31
Kontroll- und Knobelaufgaben;
Zusammenfassung
G2:
S2:
G2:
G2: 621, 622, 623,
624
G2: Gr. Z2 S. 117
617, 618, 619, 620
Gr. 6 S. 104
Gr. K2A/B S. 115/116
Probe 8.8.2
Selbstbeurteilung:
Weitere Bemerkungen zu diesem Mathplan:
Der Lehrer:
Die Eltern:
Bearbeitet am:
Geometrie : Vierecke
Geometrie : Vierecke
1
1
3
2
5
4
3
2
5
4
6
6
7
7
8
8
9
1 Quadrat :
2 Rechteck :
3 Rhombus :
4 Symm.Trapez :
5 Parallelogramm :
4 Symmetrieachsen,
4 gleichlange Seiten
2 Symmetrieachsen,
je 2 gleichlange Seiten
2 Symmetrieachsen,
4 gleichlange Seiten
1 Symmetrieachse
2 Seiten parallel
9
1 Symm.zentrum
4 rechte Winkel
1 Symm.zentrum
4 rechte Winkel
1 Symm.zentrum
1 Quadrat :
2 Seiten gleichlang
4 Symm.Trapez :
1 Symm.zentrum
paarweise parallele und gleichlange Seiten
6 Symm.Drachen : 1 Symmetrieachse
eine Diagonale wird
von der andern halbiert
7 Allgem. Trapez : 2 parallele Seiten
8 Allgem.Drachen : eine Diagonale wird von der andern halbiert
9 Allgem.Viereck : keine Seiten gleich lang oder parallel
2 Rechteck :
3 Rhombus :
5 Parallelogramm :
4 Symmetrieachsen,
4 gleichlange Seiten
2 Symmetrieachsen,
je 2 gleichlange Seiten
2 Symmetrieachsen,
4 gleichlange Seiten
1 Symmetrieachse
2 Seiten parallel
1 Symm.zentrum
4 rechte Winkel
1 Symm.zentrum
4 rechte Winkel
1 Symm.zentrum
2 Seiten gleichlang
1 Symm.zentrum
paarweise parallele und gleichlange Seiten
6 Symm.Drachen : 1 Symmetrieachse
eine Diagonale wird
von der andern halbiert
7 Allgem. Trapez : 2 parallele Seiten
8 Allgem.Drachen : eine Diagonale wird von der andern halbiert
9 Allgem.Viereck : keine Seiten gleich lang oder parallel
TEST
1.
8.8.3
Geg:
d1
d2
A
=
=
=
5,5 cm
7,2 cm
?
A
d1
d2
=
=
=
32 cm2
7 cm
?
Trapez:
Geg: A
h
p1
Ges: p2
=
=
=
=
30 cm2
4 cm
6 cm
?
Trapez:
Geg: h
p1
p2
Ges: A
=
=
=
=
38 mm
75 mm
105 mm
?
Ges:
2.
Geg:
Ges:
3.
4.
Vierecke
Name:
TEST
8.8.3
Vierecke
Name:
Resultate:
1.
Geg:
Ges:
2.
Geg:
Ges:
3.
4.
d1
d2
A
=
=
=
5,5 cm
7,2 cm
?
A
d1
d2
=
=
=
32 cm2
7 cm
?
Trapez:
Geg: A
h
p1
Ges: p2
Trapez:
Geg: h
p1
p2
Ges: A
=
=
=
=
=
=
=
=
1.
A = 19,8 cm2
2.
d2 = 9,14 cm
3.
p2 = 9 cm
4.
A = 2070 mm2
20,7 cm2
30 cm2
4 cm
6 cm
?
38 mm
75 mm
105 mm
?
4 Pt
rot
3 Pt
blau
2 Pt
gelb
8.8.2 Vielecke
Reihe A
Name:
Für die Aufgaben mit Figuren gilt:
benenne die Figur
miss und schreibe die benötigten Masse dazu (Rand gehört dazu)
stelle eine Formel für die Berechnung der Fläche auf
berechne den Flächeninhalt
0.5 Pt
0.5 Pt
0.5 Pt
0.5 Pt
1. Bezeichnung:
Formel:
Flächeninhalt:
2. Berechne das Gesuchte: 2
Trapez: Geg: A = 1000 cm
h = 4 dm
p1 = ist 1 dm länger als p2
Ges: p2 = ?
3. Bezeichnung:
Formel:
Flächeninhalt:
4. Bezeichnung:
Formel:
Flächeninhalt:
nur das Gerasterte
8.8.2 Vielecke
Reihe B
Name:
Für die Aufgaben mit Figuren gilt:
benenne die Figur
miss und schreibe die benötigten Masse dazu (Rand gehört dazu)
stelle eine Formel für die Berechnung der Fläche auf
berechne den Flächeninhalt
0.5 Pt
0.5 Pt
0.5 Pt
0.5 Pt
1. Bezeichnung:
Formel:
Flächeninhalt:
2. Berechne das Gesuchte: 2
Trapez: Geg: A = 15.6 dm
p1 = 6,0 dm
p2 = 9,6 dm
3. Bezeichnung:
Formel:
Flächeninhalt:
Ges: h = ?
4. Berechne das Gesuchte:
Trapez: Geg: A = 1000 cm 2
h = 4 dm
p1 = ist 1 dm länger als p2
Ges: p2 = ?
5. Bezeichnung:
Formel:
Flächeninhalt:
6. Berechne das Gesuchte:
Trapez: Geg: p1 = 10 cm
p2 = 30 cm 2
A = 10 dm
Ges: h = ?
7. Berechne das Gesuchte: 2
Trapez: Geg: A = 39.6 cm
p1 = 4,8 cm
p2 = 7,2 cm
Ges: h = ?
8. Bezeichnung:
Formel:
Flächeninhalt:
5. Bezeichnung:
Formel:
Flächeninhalt:
6. Berechne das Gesuchte:
Trapez: Geg: p1 = 36 cm
p2 = 42 cm
A = 9,36 dm
Ges: h = ?
7. Bezeichnung:
Formel:
Flächeninhalt:
8. Bezeichnung:
Formel:
Flächeninhalt:
nur das Gerasterte
2