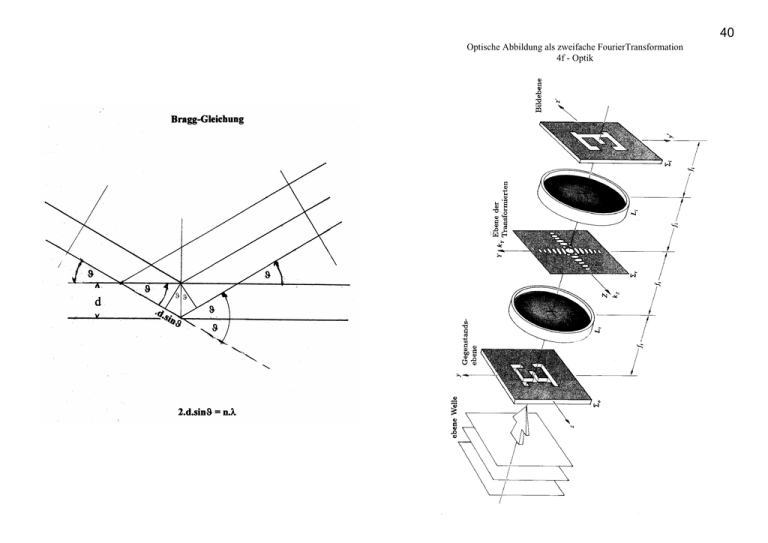
Optische Abbildung als zweifache FourierTransformation 4f

40
Optische Abbildung als zweifache FourierTransformation
4f - Optik
41
42
43
44
45
46
47
Magnetische Kernresonanz-Spektroskopie (NMR-Spektroskopie)
Nach H. Friebolin, Ein-und zweidim. N(uclear) M(agnetic) R(esonance)-Spektroskopie:
eine Einführung, 3.Aufl., Wiley-VCH, Weinheim, 1999 (ISBN 3-527-29514-3)
Bedeutung in der Chemie : Zur Strukturaufklärung von Molekülen werden an
Flüssigkeiten geringer Viskosität Spektren mit hoher Auflösung aufgenommen.
2 Nobelpreise (F.Bloch und E.M.Purcell 1952, R.R.Ernst 1991)
G
Magn. Kernmomente µ im Magnetfeld B0 am Beispiel von Protonen
Legt man an organische Moleküle äußeres Magnetfeld (in z-Richtung), tragen
die magnetischen Momente der Elektronenhüllen zu den lokalen Magnetfeldern
bei, je nach der chemischen Umgebung. Sie können aus der Orientierung der
Kernspins der Wasserstoffatome erschlossen werden.
Quantenmechanische Beschreibung durch Kernspinquantenzahl I, (Werte für I:
G
G
0, ½, 1, 3/2, 2, ...6 , für Proton 1 H gilt I = ½) mit µ = γ L , L = I ( I + 1) = ,
γ... gyroskop. Verhältnis: char. Größe für jedes Isotop (γ für Protonen besonders
groß), L... Drehimpuls = Kernspin (klass. Vorstellung: Kern rotiert um Achse).
Magn. Momente von Kernen ≈ 3 Größenordn. kleiner als von Elektronenhüllen.
Im Magnetfeld B0 gibt es bei I = ½ zwei Orientierungen des Drehimpulses (Magnetquantenzahl
m = ±½), sodass L = = 3 / 2 , Lz = m= = ± = / 2
µ z = ± γ = / 2 . Winkel(L - z-Achse) ϕ = 54,74°
und 125,26° weil cosϕ = Lz / L = ±1/ 3 .
Energien E β ,α = ± γ B0= / 2 , mit Eα < Eβ;
G
µα ,z und B0 gleichgerichtet, Differenz
∆E = E β − Eα = γ = B0 . ∆E = hν L, Larmorfrequenz (auch Präzession der µ mit ν L). Mehr
α - als β -Zustände besetzt (Boltzmannfaktor).
Durchführung des Kernresonanz-Experiments:
1) Radiofrequenz ν 1 = ν L in y-Richtung eingestrahlt, Energie-Übergänge in
beide Richtungen angeregt, Anzahl der Übergänge proportional zu
Besetzungszahlen, daher überwiegt Absorption gegenüber Emission. Empfängerantenne misst Energie und damit Absorption. Durch kontinuierliche
Veränderung der eingestrahlten Radiofrequenz und Registrierung der zugeh.
Absorption: alle Resonanzfrequenzen und ihre relativen Intensitäten bestimmt.
Die Resonanzfrequenz eines Protons hängt von seiner chemischen Umgebung
ab, so viele Frequenzen wie unterschiedliche chemische Umgebungen.
2) Pulsverfahren: alle Frequenzen gleichzeitig als Puls eingestrahlt, Pulsdauer
derart gewählt, dass mittlere magnetische Momente der Protonen aus
Feldrichtung um 90° gekippt werden und dann eine Präzessionsbewegung
ausführen. Unterschiedliche lokale Magnetfelder verursachen mehrere
überlagerte Präzessionsfrequenzen ν L, die zu einer oszillierenden
Magnetisierung führen. Diese wird registriert, die einzelnen Frequenzen durch
Fourieranalyse ermittelt. Intensitäten ergeben die relative Häufigkeiten der
jeweiligen chemischen Umgebungen.
Vorstellung zum Magnetisierungsumklapp durch Radiofrequenzpuls
Radiofrequenzeinstrahlung erzeugt Magnetfeld,
das in x-Richtung oszilliert. Es kann als Überlagerung zweier gegenläufiger um die z-Achse rotierender Magnetfelder aufgefasst werden (Bild
rechts). Die Komponente B1(l) rotiert mit gleicher Geschwindigkeit und gleichem Richtungssinn wie das magnetische Moment und nur sie
kann es beeinflussen. Man betrachtet die Beeinflussung in einem mitrotierenden Koosystem
(x’, y’, z), wirksames Feld während des Pulses
ist B0+B1(l).
Der Radiofrequenzpuls dreht die Momente von
der z-Achse weg und synchronisiert sie teilweise
auf ihrer Umlaufbahn. Beides zusammen wirkt
sich auf die makroskopische Magnetisierung
aus. Ein Impuls geeigneter Dauer kippt z.B. um
90° in die y’-Richtung oder um 180°.
Die Rückkehr der magnetischen Momente in die
Ausgangslage (Relaxation) erfolgt mit 2 charakteristischen Relaxationszeiten: für die Rückkehr
in die z-Richtung (T 1, longitudinale oder Spin -GitterRelaxationszeit) und für die Rückkehr zur Gleichverteilung in xy-Ebene T2
(transversale Relaxationszeit oder Spin-Spin-Relaxationszeit) gemäß den
Blochgleichungen:
M − M0
dM z
,
=− z
dt
T1
dM x ′
M
= − x′ ,
dt
T2
dM y ′
M ′
=− y
dt
T2
48
49
Beispiele für NMR – Spektren
CH3I 90 MHz
13
1
H - Spektrum
C H3OH 22,63 MHz
13
C - Spektrum
50