28 - Medi
Werbung
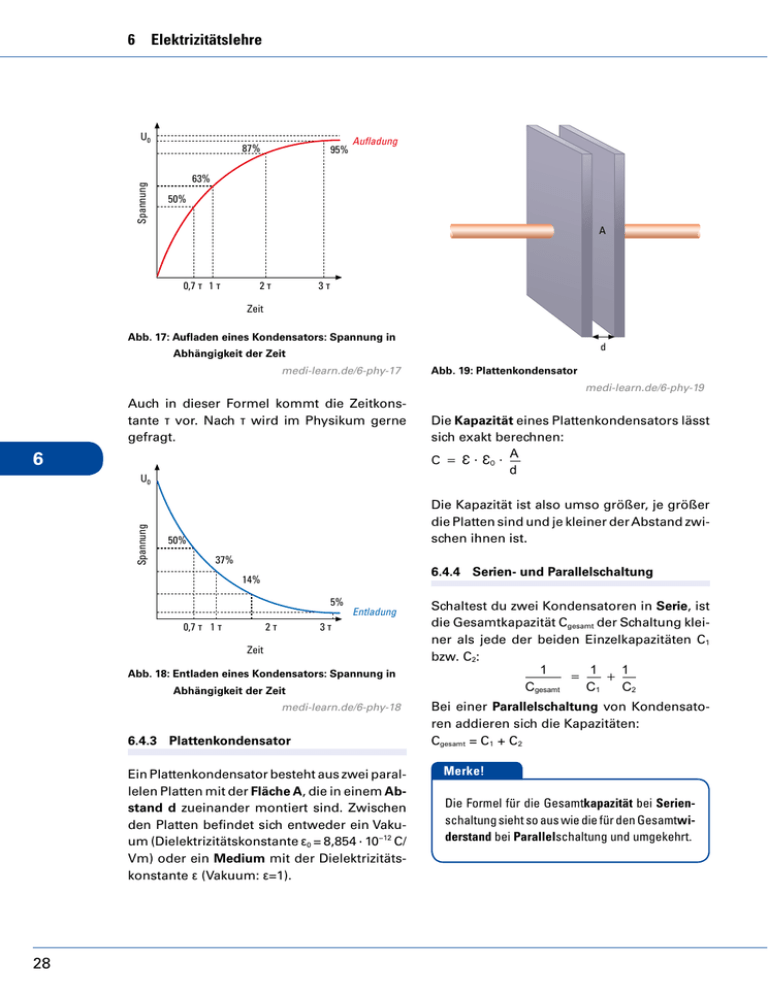
6 Elektrizitätslehre Spannung U0 95% 87% 95% Aufladung 63% 50% U0 Spannung 87% Aufladung A 63% 50%0,7 τ 1 τ 2τ 3τ Zeit Abb. 17: Aufladen eines Kondensators: Spannung in d Abhängigkeit der Zeit 0,7 τ 1 τ 2 τ medi-learn.de/6-phy-17 3τ medi-learn.de/6-phy-19 Zeit U0 Spannung Auch in dieser Formel kommt die Zeitkonstante τ vor. Nach τ wird im Physikum gerne gefragt. 6 U0 50% 37% 14% Spannung 5% 50%0,7 τ 1 τ 37% 2τ Entladung 3τ Zeit 14% 0,7 τ 1 τ Die Kapazität eines Plattenkondensators lässt sich exakt berechnen: A C = Ɛ ∙ Ɛ0 ∙ d Die Kapazität ist also umso größer, je größer die Platten sind und je kleiner der Abstand zwischen ihnen ist. 6.4.4 Serien- und Parallelschaltung 5% 2τ Entladung 3τ Zeit Abb. 18: Entladen eines Kondensators: Spannung in Abhängigkeit der Zeit medi-learn.de/6-phy-18 6.4.3 Plattenkondensator Ein Plattenkondensator besteht aus zwei paral­ lelen Platten mit der Fläche A, die in einem Abstand d zueinander montiert sind. Zwischen den Platten befindet sich entweder ein Vakuum (Dielektrizitätskonstante ε0 = 8,854 ∙ 10−12 C/ Vm) oder ein Medium mit der Dielektrizitätskonstante ε (Vakuum: ε=1). 28 Abb. 19: Plattenkondensator Schaltest du zwei Kondensatoren in Serie, ist die Gesamtkapazität Cgesamt der Schaltung kleiner als jede der beiden Einzelkapazitäten C1 bzw. C2: 1 1 1 + = C2 Cgesamt C1 Bei einer Parallelschaltung von Kondensatoren addieren sich die Kapazitäten: Cgesamt = C1 + C2 Merke! Die Formel für die Gesamtkapazität bei Serienschaltung sieht so aus wie die für den Gesamtwiderstand bei Parallelschaltung und umgekehrt.