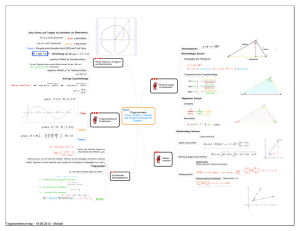
Sinus als Seitenverhältnis

Thüringer CAS-Projekt
Thema: Sinusfunktion
Martin Kesting / Wilfried Zappe
Sek I
Sek II
Schlagworte:
ClassPad™
TI-Nspire™ CAS
…….
Sinus, Seitenverhältnis, Thales, Maßübertragung
Schülermaterial:
Aufgabe – Sinus als Seitenverhältnis
Konstruiere ein veränderliches rechtwinkliges Dreieck.
Bestimme den Sinus eines Winkels durch das Seitenverhältnis.
Stelle den Sinus in Abhängigkeit vom zugehörigen Winkel grafisch dar.
Experimentiere: Bestimme den Graphen mittels „Spur“ für verschieden große
Kreise. Vergleiche!
Vorschlag zur Umsetzung:
Applikation „Geometry“ öffnen
Konstruktion Thaleskreis mit
einbeschriebenem Dreieck:
b7Punkte&Geraden 5Strecke
bAKonstruktionen3Mittelpunkt
b9 Formen1Kreis
b9 Formen2Dreieck
Einen Innenwinkel messen (Gradmaß!):
b8Messen4Winkel
Länge von Hypotenuse und Gegenkathete
messen:
b8Messen1Länge
Berechnen des Seitenverhältnisses:
a
Text b eingeben:
b1Aktionen6 Text
a
Berechnen von b :
b1Aktionen 8 Berechnen
a: Kathetenlänge  b: Hypotenusenlänge
Danach wegen der besseren Übersichtlichkeit
die Anzeige der Streckenlänge ausblenden:
/b3Auswahl
© THILLM 2010
Thema 1/3
Thüringer CAS-Projekt
b2Ansicht3Analytisches Fenster
einfügen
b4Fenster1 Fenstereinstellungen
 10  x  90 und  0 ,2  y  1
bAKonstruktion8Maßübertragung 
Winkelmaß auf x-Achse übertragen und
a
Wert von b auf y-Achse übertragen
(erst die Maßzahl, dann die Achse anklicken)
bA Konstruktion1Senkrechte 
Senkrechte durch die auf den Achsen
entstandenen Punkte konstruieren und
b7Punkte&Geraden3Schnittpunkt 
Schnittpunkt beider Senkrechten erzeugen
b5Spur4Geometriespur 
Schnittpunkt anklicken und Spitze des
Dreiecks auf dem Kreis bewegen
Didaktischer Kommentar:
Lernziele:
 Zusammenhang zwischen Definition des Sinus als Seitenverhältnis und
Sinus als Zuordnung bzw. Funktion Winkel → Sinus des Winkels klären
Lernzusammenhang:
 Trigonometrie, Einführung der Winkelfunktionen
Die Konstruktion kann als vorbereitende Hausaufgabe erledigt werden.
Bevor die Konstruktion benutzt wird, sollte man Vermutungen über das Intervall
anstellen, in dem das Seitenverhältnis liegt.
Die Geometriespur kann für verschiedene Größen des Kreises erzeugt werden.
Damit können die Schüler Einsichten über die Unabhängigkeit des
Seitenverhältnisses von der Größe des Dreiecks gewinnen.
Übungsaufgaben:

Verändere die Konstruktion so, dass das Seitenverhältnis für den
© THILLM 2010
Thema 2/3
Thüringer CAS-Projekt
Kosinus bzw. den Tangens graphisch veranschaulicht werden kann.
Untersuche auch hier, ob die Graphen von der Größe des Kreises
abhängen.

Für Freaks:
Lasse die Spur mithilfe der Animation erzeugen.
Die Spitze des Dreiecks wählen, über /b „Attribute“ wählen und dort
die Animationsgeschwindigkeit auf einen Wert größer Null setzen,
Doppelklick und dann die Spur des Schnittpunktes im analytischen
Fenster erzeugen.

Verändere die Konstruktion so, dass das Seitenverhältnis für den
Kosinus bzw. den Tangens graphisch veranschaulicht werden kann.
Untersuche auch hier, ob die Graphen von der Größe des Kreises
abhängen.
© THILLM 2010
Thema 3/3