Sinus und Kosinus im Einheitskreis - lehrer.uni

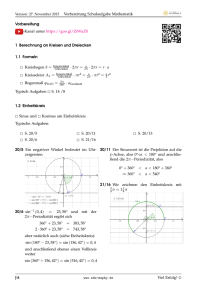
LGÖ ks
VMa 12
Schuljahr 2016/2017
Sinus und Kosinus im Einheitskreis
Sinus und Kosinus im rechtwinkligen Dreieck
Für einen Winkel ϕ mit 0° ≤ ϕ ≤ 90° gilt:
H
sin ϕ =
G
H
cos ϕ =
A
H
G
ϕ
A
Sinus und Kosinus im Einheitskreis
Zeichne in einem Koordinatensystem den Kreis um
den Ursprung mit dem Radius 1 (Einheitskreis).
y
1
yP
Zeichne den Winkel ϕ mit dem Ursprung als Scheitel
und der positiven x-Achse als erstem Schenkel.
P
1
ϕ
Nenne den Schnittpunkt des zweiten Schenkels mit dem
Einheitskreis P.
sin=
ϕ
yP
= yP
1
cos=
ϕ
xP
= xP
1
x
xP
Merke:
1
y
1
sin ϕ
sin ϕ = y -Koordinate von P
P
cos ϕ = x-Koordinate von P
ϕ
Das nimmt man als Definition für den Sinus und den
Kosinus eines Winkels, der negativ oder größer als 90°
ist.
cos ϕ
Beispiel: Bestimme zeichnerisch (näherungsweise):
sin 140° ≈ 0, 6
cos 140° ≈ −0,8
y
1
140°
1
sinusundkosinusimeinheitskreis
x
x
1