Trigonometrie - Sinus, Kosinus, Tangens und Zusammenhänge am

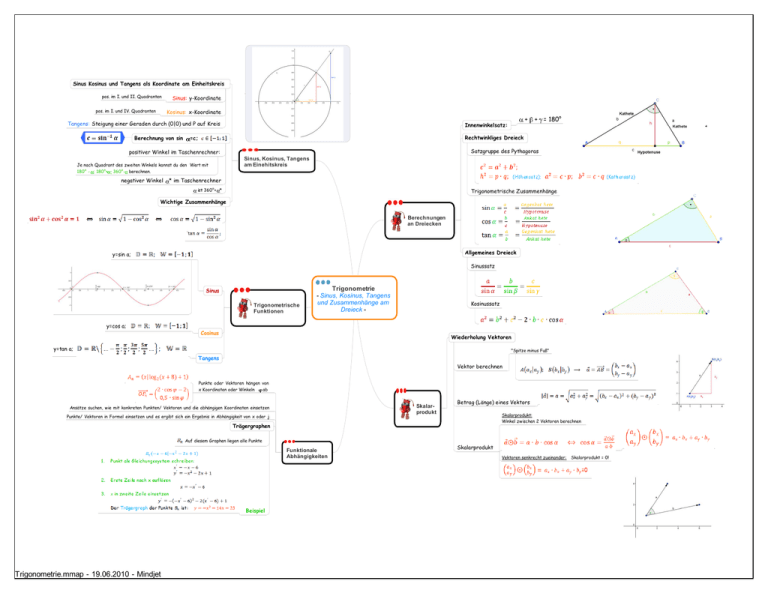
Sinus Kosinus und Tangens als Koordinate am Einheitskreis
pos. im I. und II. Quadranten
pos. im I. und IV. Quadranten
Sinus: y-Koordinate
Kosinus: x-Koordinate
Tangens: Steigung einer Geraden durch (0|0) und P auf Kreis
Berechnung von sin
+ = 180°
Rechtwinkliges Dreieck
=c;
Satzgruppe des Pythagoras
positiver Winkel im Taschenrechner:
Je nach Quadrant des zweiten Winkels kannst du den Wert mit
180° - ; 180°+ 360°- berechnen.
negativer Winkel
+
Innenwinkelsatz:
Sinus, Kosinus, Tangens
am Einehitskreis
* im Taschenrechner
ist 360°+ *
Trigonometrische Zusammenhänge
Wichtige Zusammenhänge
Berechnungen
an Dreiecken
Allgemeines Dreieck
y=sin a;
Sinussatz
Sinus
Trigonometrische
Funktionen
y=cos a;
Trigonometrie
- Sinus, Kosinus, Tangens
und Zusammenhänge am
Dreieck -
Kosinussatz
Cosinus
Wiederholung Vektoren
y=tan a;
"Spitze minus Fuß"
Tangens
Vektor berechnen
Punkte oder Vektoren hängen von
ab
x Koordinaten oder Winkeln
Skalarprodukt
Ansätze suchen, wie mit konkreten Punkten/ Vektoren und die abhängigen Koordinaten einsetzen
Punkte/ Vektoren in Formel einsetzen und es ergibt sich ein Ergebnis in Abhängigkeit von x oder j
Betrag (Länge) eines Vektors
Skalarprodukt:
Winkel zwischen 2 Vektoren berechnen
Trägergraphen
Auf diesem Graphen liegen alle Punkte
Funktionale
Abhängigkeiten
Beispiel
Trigonometrie.mmap - 19.06.2010 - Mindjet
Skalarprodukt
Vektoren senkrecht zueinander:
Skalarprodukt = 0!